Содержание
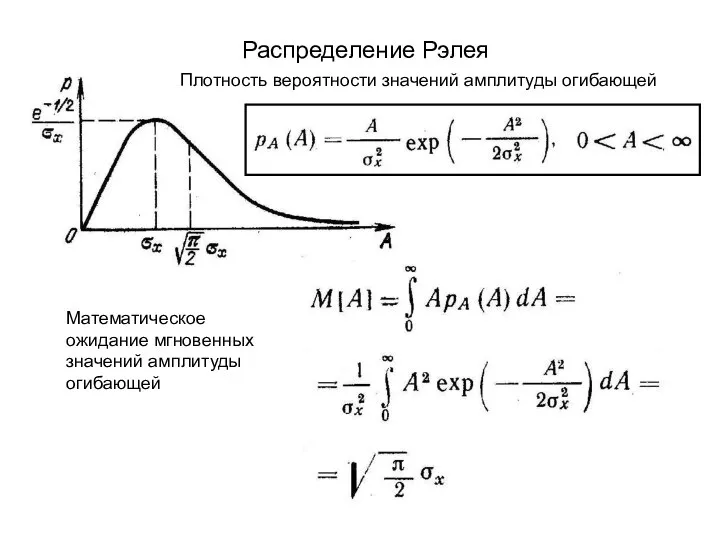
- 2. Распределение Рэлея Плотность вероятности значений амплитуды огибающей Математическое ожидание мгновенных значений амплитуды огибающей
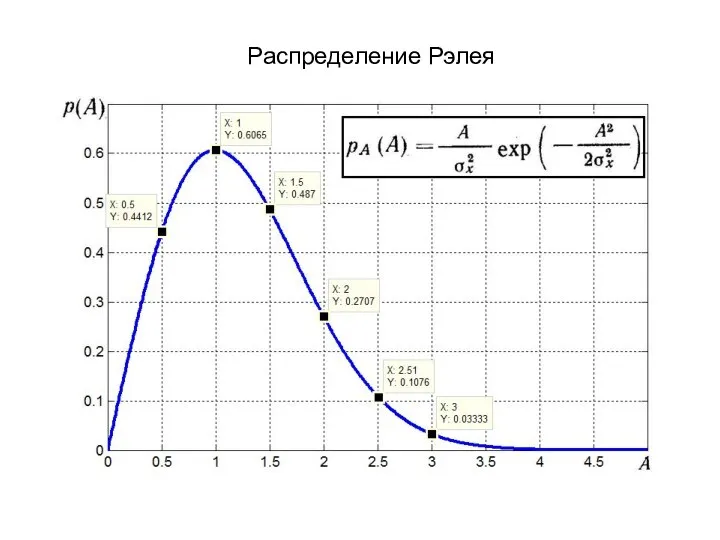
- 3. Распределение Рэлея
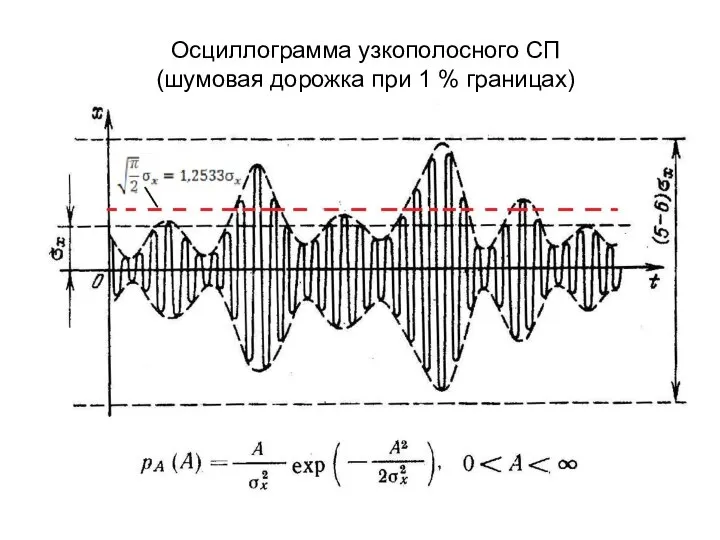
- 4. Осциллограмма узкополосного СП (шумовая дорожка при 1 % границах)
- 5. 8. Огибающая суммы гармонического сигнала и узкополосного нормального шума В радиотехнике часто интересуются статистическими свойствами сигнала,
- 6. Огибающая суммы гармонического сигнала и узкополосного нормального шума Очевидно, между парами имеется связь: Якобиан D этого
- 7. Огибающая суммы гармонического сигнала и узкополосного нормального шума Проинтегрируем правую часть формулы по угловой координате: в
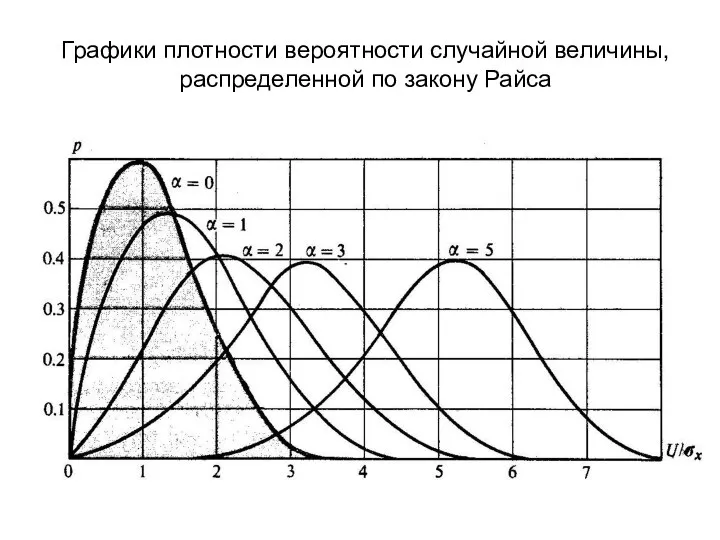
- 8. Огибающая суммы гармонического сигнала и узкополосного нормального шума Ниже представлены графики плотности вероятности случайной величины, распределенной
- 9. Графики плотности вероятности случайной величины, распределенной по закону Райса
- 10. Огибающая суммы гармонического сигнала и узкополосного нормального шума Практически считают, что уже при огибающая результирующего сигнала
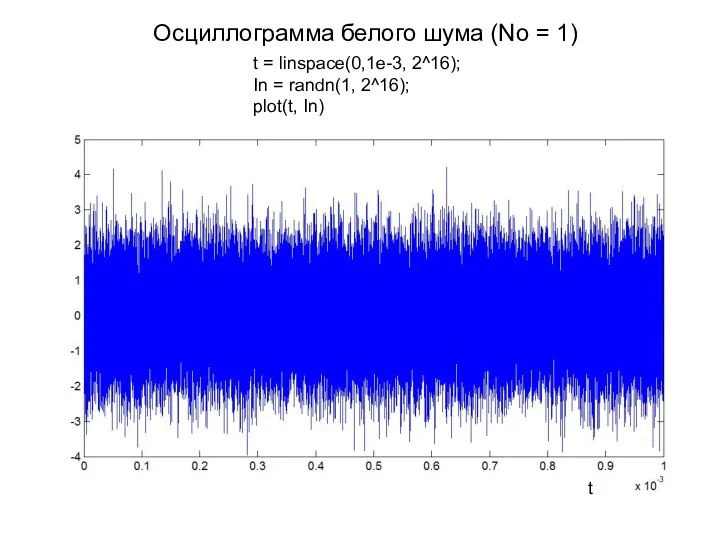
- 11. Осциллограмма белого шума (No = 1) t = linspace(0,1e-3, 2^16); In = randn(1, 2^16); plot(t, In)
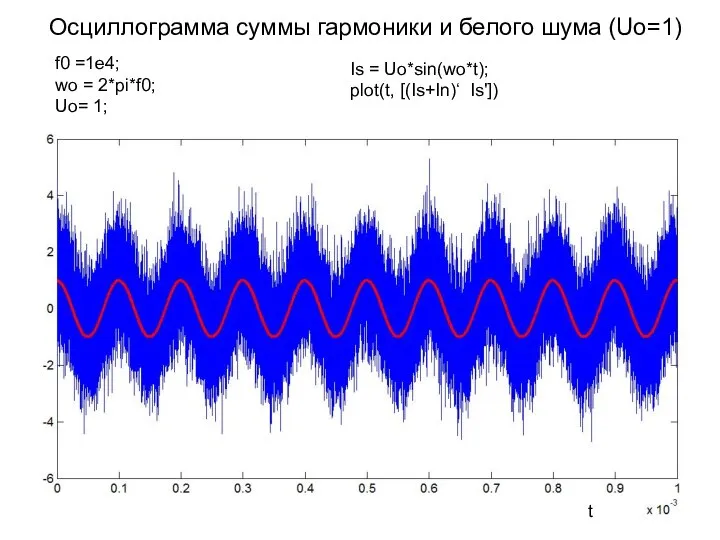
- 12. Осциллограмма суммы гармоники и белого шума (Uo=1) f0 =1e4; wo = 2*pi*f0; Uo= 1; Is =
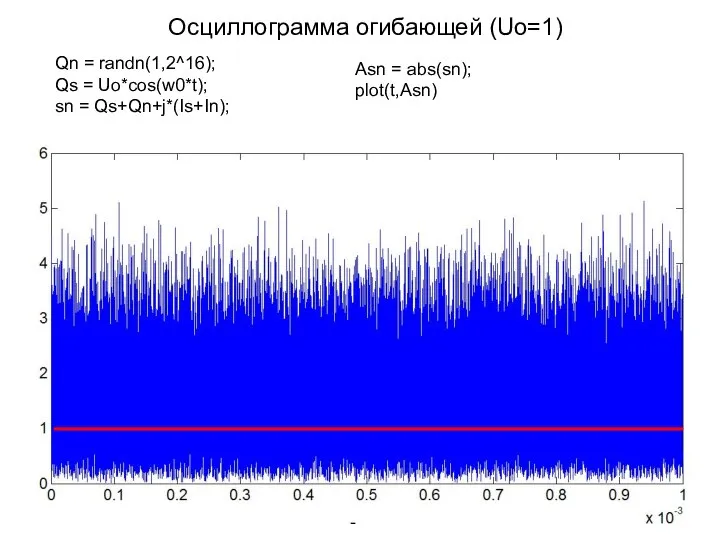
- 13. Осциллограмма огибающей (Uo=1) Qn = randn(1,2^16); Qs = Uo*cos(w0*t); sn = Qs+Qn+j*(Is+In); Asn = abs(sn); plot(t,Asn)
- 14. Гистограмма огибающей суммы гармоники и белого шума [n,x] = hist(Asn,50); bar(x, n/2^16) S+n
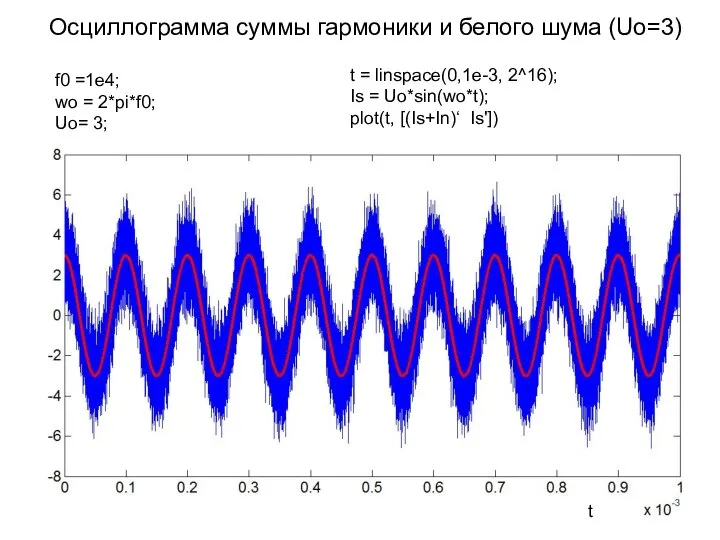
- 15. Осциллограмма суммы гармоники и белого шума (Uo=3) f0 =1e4; wo = 2*pi*f0; Uo= 3; t =
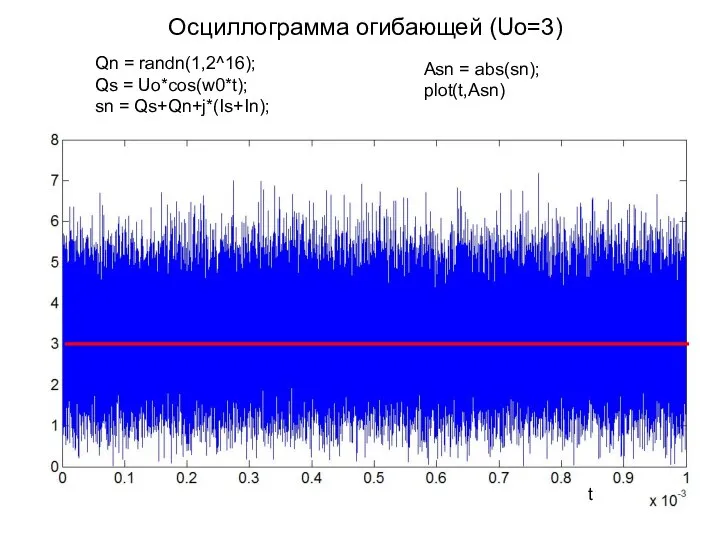
- 16. Осциллограмма огибающей (Uo=3) Qn = randn(1,2^16); Qs = Uo*cos(w0*t); sn = Qs+Qn+j*(Is+In); Asn = abs(sn); plot(t,Asn)
- 17. Гистограмма огибающей суммы гармоники и белого шума [n,x] = hist(Asn,50); bar(x, n/2^16) S+n
- 18. 8.2. Интервал корреляции Числовой характеристикой, служащей для оценки «скорости изменения» реализаций случайного процесса, является интервал корреляции
- 19. 8.3. Эффективная ширина спектра Пусть исследуемый случайный процесс характеризуется функцией - односторонним спектром мощности, причем —
- 20. Пример Здесь высокочастотный сомножитель имеет период 106 с, амплитудный сомножитель изменяется за это время лишь в
- 21. 8.4. Белый шум В радиотехнике так принято называть стационарный случайный процесс с постоянной на всех частотах
- 22. Белый шум Средняя мощность (дисперсия) белого шума неограниченно велика. Белый шум является дельта-коррелированным случайным процессом. Некоррелированность
- 23. 8.5. Дифференцирование и интегрирование случайных процессов Дифференциальные свойства случайного процесса определяются видом его функции корреляции. Предположим,
- 24. Дифференцирование случайных процессов Пусть математическое ожидание исходного процесса (если это не так, то всегда можно перейти
- 25. Дифференцирование случайных процессов Все четыре слагаемых в квадратных скобках представляют собой функции корреляции исходного процесса, вычисленные
- 26. 8.6. Дифференцируемые и недифференцируемые случайные процессы По определению, случайный процесс X(t) является дифференцируемым, если его производная
- 27. Дифференцируемые и недифференцируемые случайные процессы Реализации любых случайных сигналов, с которыми приходится встречаться в технике, всегда
- 28. 8.7. Спектральная плотность мощности производной Найдем связь между спектрами мощности исходного процесса и его производной. Пусть
- 29. 8.8. Корреляционная связь между случайным процессом и его производной Во многих задачах статистической радиотехники существен вопрос
- 30. Корреляционная связь между случайным процессом и его производной Как известно, функция Rx(т) всегда является четной. Если
- 31. 8.9. Интеграл от случайного процесса Будем называть случайный процесс Z(t) определенным интегралом с переменным верхним пределом
- 32. Интеграл от случайного процесса Однако даже при нулевом математическом ожидании входного процесса сигнал на выходе интегратора
- 33. Интеграл от случайного процесса Нестационарность интеграла от случайного процесса имеет глубокий физический смысл, свидетельствуя о безграничном
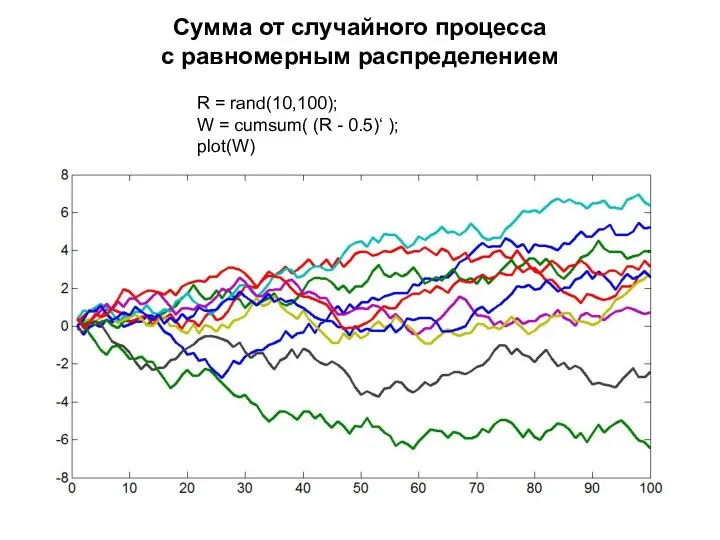
- 34. Сумма от случайного процесса с равномерным распределением R = rand(10,100); W = cumsum( (R - 0.5)‘
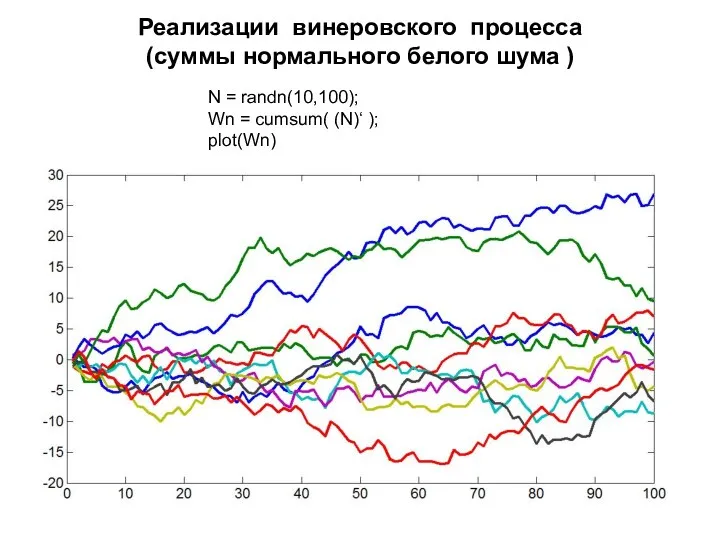
- 35. Реализации винеровского процесса (суммы нормального белого шума ) N = randn(10,100); Wn = cumsum( (N)‘ );
- 36. 8.10. Шумоподобный сигнал В радиотехнике помимо узкополосных повсеместное применение находят и широкополосные сигналы. К числу последних
- 37. Шумоподобный сигнал Шумоподобные сигналы используются: – при кодовой адресации большого числа абонентов и их кодовом раз
- 38. Формирование шумоподобного сигнала Для формирования которого используются, в основном, два способа — дискретной фазовой и частотной
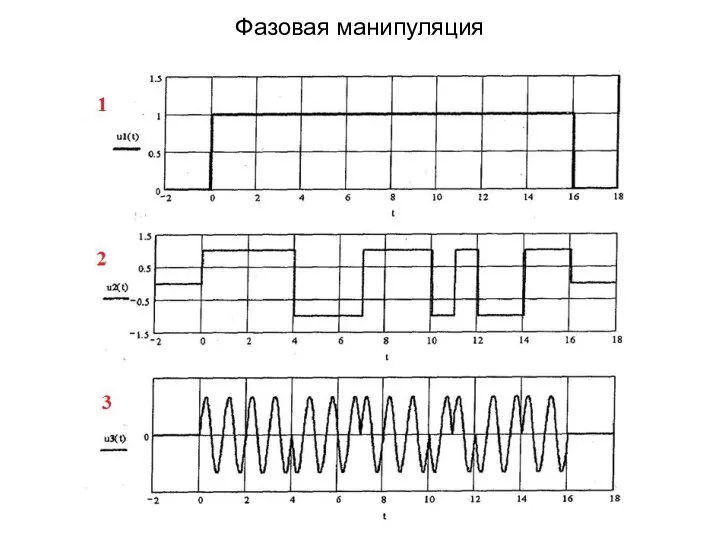
- 39. Фазовая манипуляция
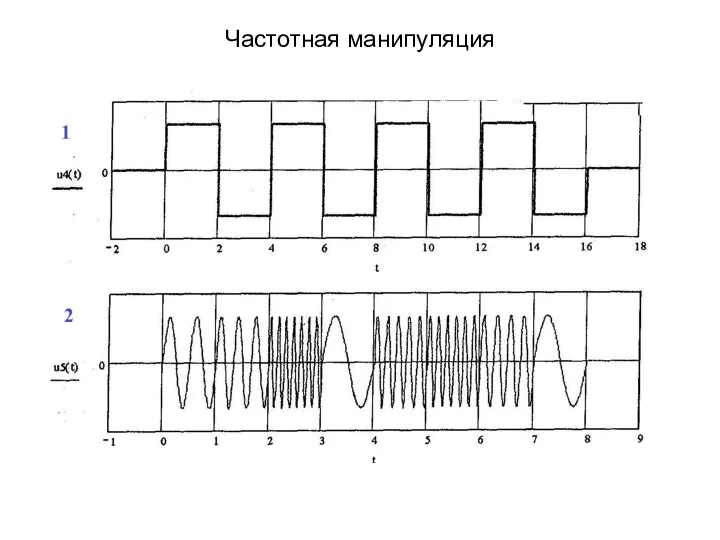
- 40. Частотная манипуляция
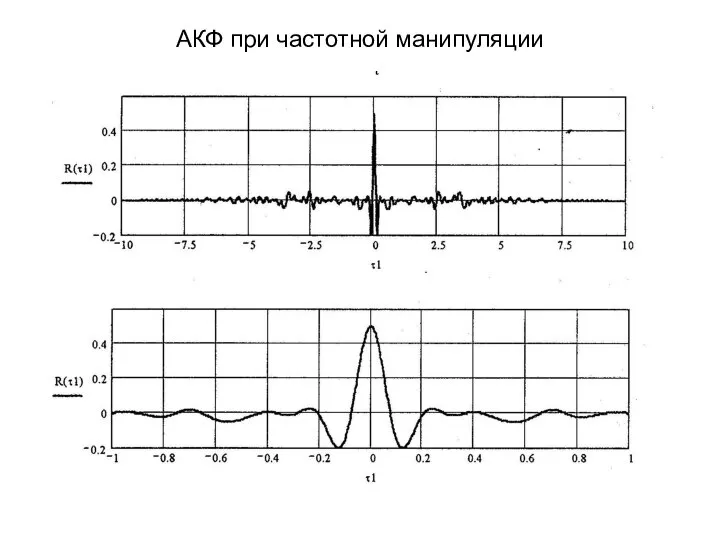
- 41. АКФ при частотной манипуляции
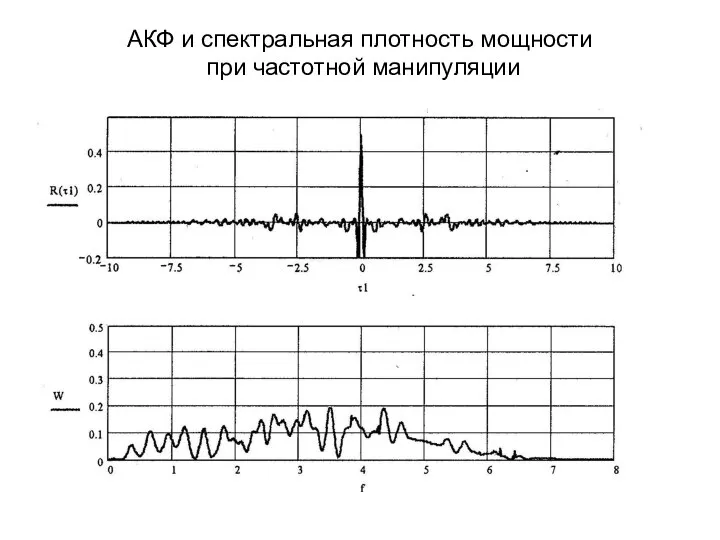
- 42. АКФ и спектральная плотность мощности при частотной манипуляции
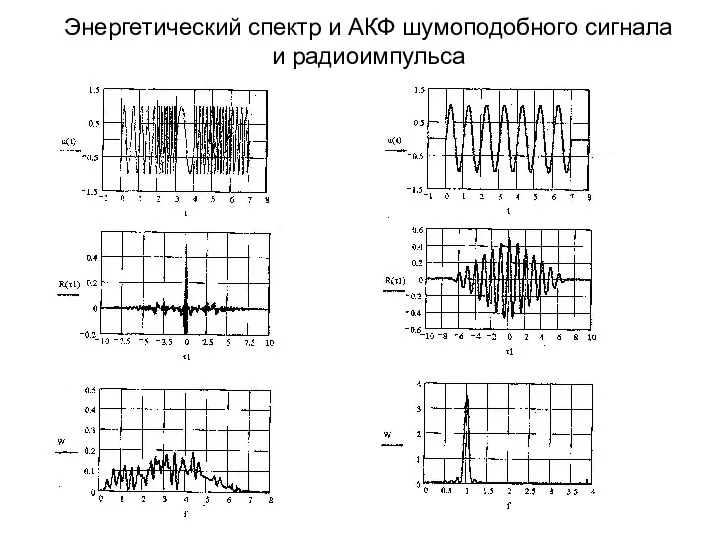
- 43. Энергетический спектр и АКФ шумоподобного сигнала и радиоимпульса
- 45. Скачать презентацию





![Гистограмма огибающей суммы гармоники и белого шума [n,x] = hist(Asn,50); bar(x, n/2^16) S+n](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1292910/slide-13.jpg)
![Гистограмма огибающей суммы гармоники и белого шума [n,x] = hist(Asn,50); bar(x, n/2^16) S+n](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1292910/slide-16.jpg)



















 Презентация "Стратегия российского бизнеса в условиях вступления России в ВТО" - скачать презентации по Экономике
Презентация "Стратегия российского бизнеса в условиях вступления России в ВТО" - скачать презентации по Экономике Форма государства: форма правления, форма государственного устройства и форма политического режима
Форма государства: форма правления, форма государственного устройства и форма политического режима Работа с дефектами в IT
Работа с дефектами в IT Презентация "Архитектурные памятники Белгорода" - скачать презентации по МХК
Презентация "Архитектурные памятники Белгорода" - скачать презентации по МХК Гимнастика. Спортивные снаряды
Гимнастика. Спортивные снаряды Lubrication engine
Lubrication engine Здоровая страна начинается с тебя
Здоровая страна начинается с тебя Англиканство. Генрих XVIII
Англиканство. Генрих XVIII Блоктық шифрлар үшін дифференциалдық криптоталдау тәсілдерімен орнықтылықты зерттеу
Блоктық шифрлар үшін дифференциалдық криптоталдау тәсілдерімен орнықтылықты зерттеу Холецистит
Холецистит  Управление разграничением доступа в базах данных
Управление разграничением доступа в базах данных Статистика национального богатства
Статистика национального богатства Презентация "Фитодизайн" - скачать презентации по МХК
Презентация "Фитодизайн" - скачать презентации по МХК Лекція № 13 ОРГАНІЗАЦІЯ МАРКЕТИНГУ НА ПІДПРИЄМСТВІ
Лекція № 13 ОРГАНІЗАЦІЯ МАРКЕТИНГУ НА ПІДПРИЄМСТВІ  Источники техногенного воздействия на геологическую среду в нефтегазовом производстве. Экологическая безопасность
Источники техногенного воздействия на геологическую среду в нефтегазовом производстве. Экологическая безопасность Моделирование соревновательных ситуаций в процессе технико-тактической подготовки самбистов возрастной группы 18 лет-23 года
Моделирование соревновательных ситуаций в процессе технико-тактической подготовки самбистов возрастной группы 18 лет-23 года Omówienie działań, proektów kierowanych do uznanych mniejszości narodowych, etnicznych i językowych w Polsce
Omówienie działań, proektów kierowanych do uznanych mniejszości narodowych, etnicznych i językowych w Polsce Жостовская роспись
Жостовская роспись Почечное кровообращение
Почечное кровообращение  Духовная культура общества
Духовная культура общества Арифметические действия над числами. ( урок 32) Презентация к уроку математики 3 класс УМК «Школа 2100»
Арифметические действия над числами. ( урок 32) Презентация к уроку математики 3 класс УМК «Школа 2100»  Презентация на тему "Портфолио учителя математики" - скачать презентации по Педагогике
Презентация на тему "Портфолио учителя математики" - скачать презентации по Педагогике Методологические подходы в психологии
Методологические подходы в психологии «Технология построения современного урока».
«Технология построения современного урока». Рост и развитие хлебных злаков
Рост и развитие хлебных злаков  Алгоритм шифрования DES
Алгоритм шифрования DES ПРЕЗЕНТАЦИЯ ДЛЯ УРОКА МИРОВОЙ ХУДОЖЕСТВЕННОЙ КУЛЬТУРЫ ТЕМА: «ЯРКИЕ ПРЕДСТАВИТЕЛИ АРХИТЕКТУРЫ СТИЛЯ АМПИР»
ПРЕЗЕНТАЦИЯ ДЛЯ УРОКА МИРОВОЙ ХУДОЖЕСТВЕННОЙ КУЛЬТУРЫ ТЕМА: «ЯРКИЕ ПРЕДСТАВИТЕЛИ АРХИТЕКТУРЫ СТИЛЯ АМПИР»  Чемпионы паралимпийских игр
Чемпионы паралимпийских игр