Содержание
- 2. 1. ОПРЕДЕЛЕНИЕ ФОРМУЛЫ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ Математическая логика стремится к возможно большей точности. Эта цель достигается с
- 3. 1. ОПРЕДЕЛЕНИЕ ФОРМУЛЫ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ Будем полагать, что высказывания удовлетворяют закону исключенного третьего и закону непротиворечия,
- 4. 1. ОПРЕДЕЛЕНИЕ ФОРМУЛЫ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ С помощью констант (связок) атомарные высказывания соединяются в более сложные высказывания.
- 5. 1. ОПРЕДЕЛЕНИЕ ФОРМУЛЫ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ Переменные и сложные высказывания, образованные из них посредствам многократного применения логических
- 6. 1. ОПРЕДЕЛЕНИЕ ФОРМУЛЫ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ Для того, чтобы избежать слишком, большое количество скобок принимаются следующее соглашение:
- 7. 2. АЛГЕБРА ВЫСКАЗЫВАНИЙ Любая формула алгебры высказываний рассматривается как сложное высказывание, принимающее значение 0,1. В алгебре
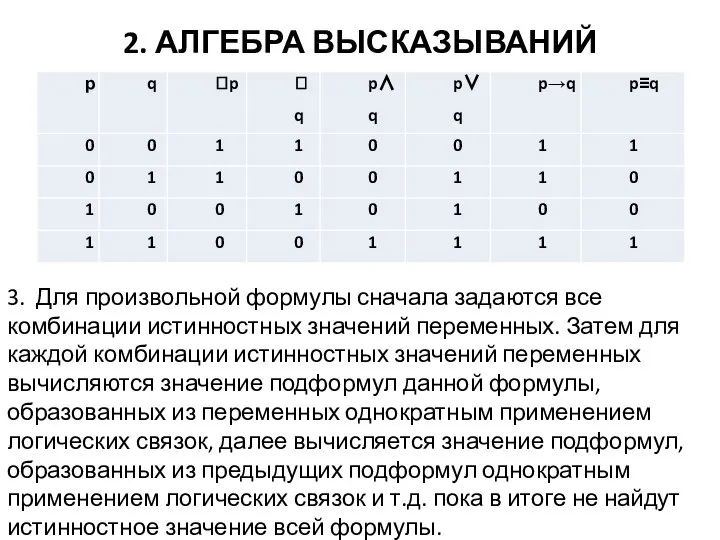
- 8. 2. АЛГЕБРА ВЫСКАЗЫВАНИЙ 3. Для произвольной формулы сначала задаются все комбинации истинностных значений переменных. Затем для
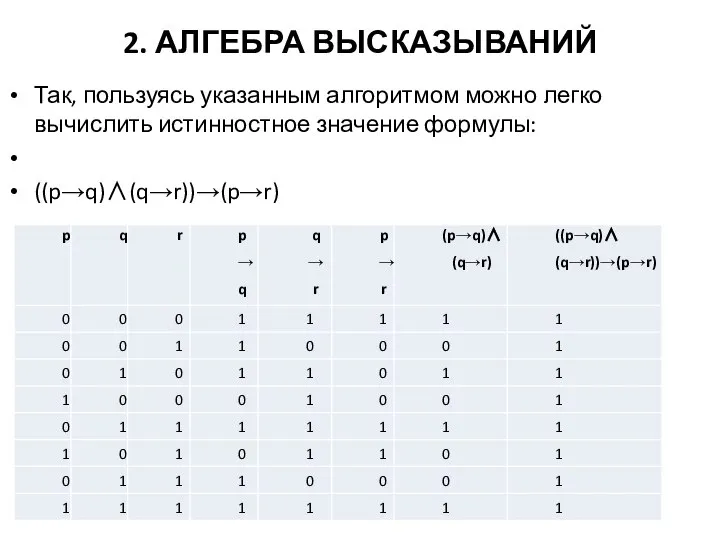
- 9. 2. АЛГЕБРА ВЫСКАЗЫВАНИЙ Так, пользуясь указанным алгоритмом можно легко вычислить истинностное значение формулы: ((p→q)∧(q→r))→(p→r)
- 10. 2. АЛГЕБРА ВЫСКАЗЫВАНИЙ Каждой формуле исчисления высказываний соответствует определенная функция, аргументы которой принимают значение из множества
- 11. 2. АЛГЕБРА ВЫСКАЗЫВАНИЙ Это проблема полностью решается посредствам вычисления значения функции, представленной данной формулой, с помощью
- 12. 2. АЛГЕБРА ВЫСКАЗЫВАНИЙ Аналогичным образом убеждаемся, что функция р∧p тоже выражается логический закон: закон непротиворечия:
- 13. 3. ЗАКОНЫ ЛОГИКИ С помощью таблиц истинности можно убедится, что нижеприведенные функции выражают логические законы. Запишем
- 14. 3. ЗАКОНЫ ЛОГИКИ Закон идемпотентности: для конъюнкции: р∧р ≡ р (3) для дизъюнкции: р∨ р ≡
- 15. 3. ЗАКОНЫ ЛОГИКИ Закон поглощения: для конъюнкции дизъюнкций: р∧( q ∨р) ≡ p (7) для дизъюнкции
- 16. Вопросы Перечислите 8 этапов подготовки и решения задач на ЭВМ Чему следует уделять первостепенное внимание при
- 18. Скачать презентацию













 ВКР:Особенности правового регулирования труда отдельных категорий работников
ВКР:Особенности правового регулирования труда отдельных категорий работников Кафедра ветеринарной хирургии Лекция РАНЫ и раневой процесс
Кафедра ветеринарной хирургии Лекция РАНЫ и раневой процесс  ПРИОБРЕТЕНИЕ МУНИЦИПАЛЬНЫМИ ОБРАЗОВАНИЯМИ ПРАВА СОБСТВЕННОСТИ НА БЕСХОЗЯЙНЫЕ НЕДВИЖИМЫЕ ВЕЩИ И НАСЛЕДОВАНИЕ ВЫМОРОЧНОГО ИМУ
ПРИОБРЕТЕНИЕ МУНИЦИПАЛЬНЫМИ ОБРАЗОВАНИЯМИ ПРАВА СОБСТВЕННОСТИ НА БЕСХОЗЯЙНЫЕ НЕДВИЖИМЫЕ ВЕЩИ И НАСЛЕДОВАНИЕ ВЫМОРОЧНОГО ИМУ 2010 г.
2010 г. Модная и красивая. Фотоальбом
Модная и красивая. Фотоальбом Тема урока: сочинение-описание памятника архитектуры Храм Василия Блаженного 8 класс Цели урока: продолжить знакомство с арх
Тема урока: сочинение-описание памятника архитектуры Храм Василия Блаженного 8 класс Цели урока: продолжить знакомство с арх Лабораторная диагностика стафилококковых, стрептококковых, менингококковой инфекций.
Лабораторная диагностика стафилококковых, стрептококковых, менингококковой инфекций. ОБРАЗОВАТЕЛЬНАЯ СИСТЕМА «ШКОЛА 2100» - И ЕЕ ГОТОВНОСТЬ К ФГОС
ОБРАЗОВАТЕЛЬНАЯ СИСТЕМА «ШКОЛА 2100» - И ЕЕ ГОТОВНОСТЬ К ФГОС «Основные понятия и принципы системного подхода» Подготовила студентка Житкова Екатерина 1 курса экономического факультета гру
«Основные понятия и принципы системного подхода» Подготовила студентка Житкова Екатерина 1 курса экономического факультета гру Номенклатура справ
Номенклатура справ Операторы цикла
Операторы цикла Чемпионат мира по хоккею с шайбой 2016
Чемпионат мира по хоккею с шайбой 2016 Презентация "Культура античности.Эгейское искусство" - скачать презентации по МХК
Презентация "Культура античности.Эгейское искусство" - скачать презентации по МХК Аксонометрия
Аксонометрия [email protected] /5 CapSense
[email protected] /5 CapSense Геохимические процессы в системе природная вода – горная порода 1
Геохимические процессы в системе природная вода – горная порода 1 Политология как наука
Политология как наука ГЕОЛОГИЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ ВЕТРА
ГЕОЛОГИЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ ВЕТРА Судебное заседание
Судебное заседание украинские казаки
украинские казаки  Нетрадиционные методы отбора персонала
Нетрадиционные методы отбора персонала Посібник-конструктор для вчителів української мови. Навчальні таблиці
Посібник-конструктор для вчителів української мови. Навчальні таблиці Основы теории всеобщего управления качеством (tqm) Принципы tqm СМК. Школа качества и управления. Занятие 2 Отдел маркетинга и иннов
Основы теории всеобщего управления качеством (tqm) Принципы tqm СМК. Школа качества и управления. Занятие 2 Отдел маркетинга и иннов Разработка плана ликвидации последствий ЧС
Разработка плана ликвидации последствий ЧС олимпийские игры Бадминтон
олимпийские игры Бадминтон Небо надо мной синеет. Ты со мной, мой Господь
Небо надо мной синеет. Ты со мной, мой Господь Мейрамы наурыз
Мейрамы наурыз Римско-католический приход Воздвижение Святого Креста
Римско-католический приход Воздвижение Святого Креста