Содержание
- 2. Распишем второе уравнение через косинус суммы, подставляя при этом вместо cosωt и sinωt их значения (25.3.3)
- 3. Последнее уравнение есть, вообще говоря, уравнение эллипса, оси которого повернуты относительно координатных осей х и y.
- 4. Рис. 25.6 Рис. 25.7
- 5. т.е. уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний. Случай эллиптически
- 7. Рис. 25.9 Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет вид довольно
- 8. Рис. 25.10 Рис. 25.11
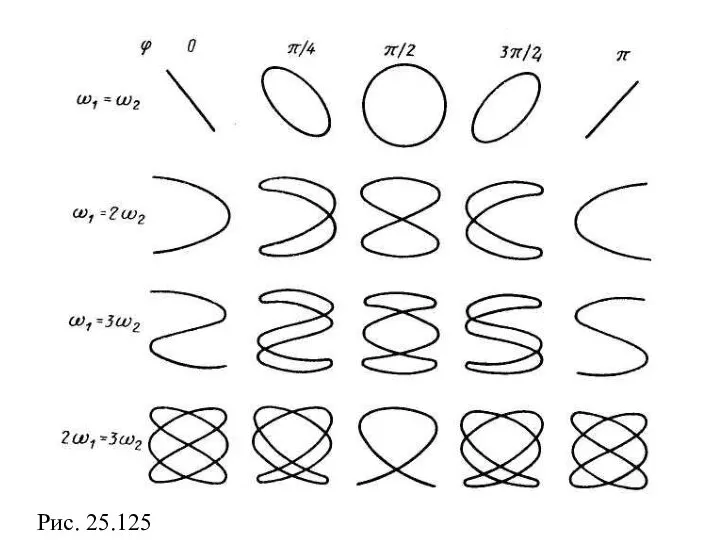
- 9. Рис. 25.125
- 11. Скачать презентацию
Слайд 2
Распишем второе уравнение через косинус суммы, подставляя при этом вместо cosωt
Распишем второе уравнение через косинус суммы, подставляя при этом вместо cosωt
и sinωt их значения (25.3.3) и (25.3.3,a):
y/а2 = cosωt⋅cosΔα - sinωt⋅ sinΔα
= (x/а1) cosΔα - (± sinΔα(√1 – x2/а12))
Перепишем
(y/а2 – (x/а1)cosΔα)2 = (-sinΔα√1-x2/а12 )2
Возведем обе части в квадрат
y2/а22 +(x2/а12 )⋅cos2Δα - (2xy/а1а2)⋅cosΔα =
sin2Δα - (x2/ а12)⋅sin2Δα
y2/a22 + (x2/a12)(cos2Δα + sin2Δα) – (2xy/a1a2)⋅cosΔα = sin2Δα
y2/a22 + x2/a12 – (2xy/a1a2)⋅cosΔα = sin2Δα
В общем, виде
y2/a22 +x2/a12- (2xy/a1a2)⋅ cos(α2 - α1 ) = sin2(α2 - α1) (3.4)
y/а2 = cosωt⋅cosΔα - sinωt⋅ sinΔα
= (x/а1) cosΔα - (± sinΔα(√1 – x2/а12))
Перепишем
(y/а2 – (x/а1)cosΔα)2 = (-sinΔα√1-x2/а12 )2
Возведем обе части в квадрат
y2/а22 +(x2/а12 )⋅cos2Δα - (2xy/а1а2)⋅cosΔα =
sin2Δα - (x2/ а12)⋅sin2Δα
y2/a22 + (x2/a12)(cos2Δα + sin2Δα) – (2xy/a1a2)⋅cosΔα = sin2Δα
y2/a22 + x2/a12 – (2xy/a1a2)⋅cosΔα = sin2Δα
В общем, виде
y2/a22 +x2/a12- (2xy/a1a2)⋅ cos(α2 - α1 ) = sin2(α2 - α1) (3.4)
Слайд 3
Последнее уравнение есть, вообще говоря, уравнение эллипса, оси которого повернуты относительно
Последнее уравнение есть, вообще говоря, уравнение эллипса, оси которого повернуты относительно
координатных осей х и y.
Ориентация эллипса и величина его полуосей зависят довольно сложным образом от амплитуд а1 и а2 и разности фаз α.
Определим форму траектории для некоторых частных случаев.
1) Начальные фазы колебаний одинаковы α1 = α2 т.е. α2 - α1 = 0
Тогда уравнение имеет вид y2/a22 +x2/a12- 2xy/a1a2 = 0
или (x/а1 - y/а2)2 =0 или x/а1 = y/а2
или x/y =а1 /а2 или y= (а1 /а2) ⋅x (3.5)
(Это уравнение прямой, проходящей через начало координат)
Следовательно, в результате сложения двух взаимно перпендикулярных колебаний с одинаковыми начальными фазами колебания будут происходить вдоль прямой, проходящей через начало координат.
Такие колебания называются линейно поляризованными.
Ориентация эллипса и величина его полуосей зависят довольно сложным образом от амплитуд а1 и а2 и разности фаз α.
Определим форму траектории для некоторых частных случаев.
1) Начальные фазы колебаний одинаковы α1 = α2 т.е. α2 - α1 = 0
Тогда уравнение имеет вид y2/a22 +x2/a12- 2xy/a1a2 = 0
или (x/а1 - y/а2)2 =0 или x/а1 = y/а2
или x/y =а1 /а2 или y= (а1 /а2) ⋅x (3.5)
(Это уравнение прямой, проходящей через начало координат)
Следовательно, в результате сложения двух взаимно перпендикулярных колебаний с одинаковыми начальными фазами колебания будут происходить вдоль прямой, проходящей через начало координат.
Такие колебания называются линейно поляризованными.
Слайд 4
Рис. 25.6
Рис. 25.7
Рис. 25.6
Рис. 25.7
Слайд 5
т.е. уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны
т.е. уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны
соответствующим амплитудам колебаний. Случай эллиптически поляризованных колебаний. При равенстве амплитуд а1 и а2 эллипс вырождается в окружность.
Случаи α = + π/2 и α = -π/2 отличаются направлением движения по эллипсу или по окружности. Если α = +π/2 , уравнение (3.7) можно записать следующим образом:
х = а1cosωt и y = -а2sinωt . (3.8)
В момент времени t = 0 тело находится в точке 1 (рис. 25.8). В последующие моменты времени координата х уменьшается, а координата у становится отрицательной. Следовательно, движение совершается по часовой стрелке. Если α = -π/2 , уравнение (3.7)
Случаи α = + π/2 и α = -π/2 отличаются направлением движения по эллипсу или по окружности. Если α = +π/2 , уравнение (3.7) можно записать следующим образом:
х = а1cosωt и y = -а2sinωt . (3.8)
В момент времени t = 0 тело находится в точке 1 (рис. 25.8). В последующие моменты времени координата х уменьшается, а координата у становится отрицательной. Следовательно, движение совершается по часовой стрелке. Если α = -π/2 , уравнение (3.7)
Рис. 25.8
можно записать следующим образом:
х = а1cosωt и y = +а2sinωt . (3.8)
Отсюда можно заключить, что движение происходит против часовой стрелки.
Слайд 6
Слайд 7
Рис. 25.9
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория
Рис. 25.9
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория
результирующего движения имеет вид
довольно сложных кривых, называемых фигурами Лиссажу. На рис. 25.9 показана одна из простейших траекторий. Получающаяся при отношении частот 1:2 и разности фаз π/2. Уравнения колебаний имеют вид
х = аcosωt и y = bcos(2ωt+ π/2) (3.11)
За то время, пока вдоль оси х точка успевает пройти из одного крайнего положения в другое, вдоль оси у, выйдя из нулевого положения, она успевает достигнуть одного крайнего положения, затем другого и вернуться в нулевое положение.
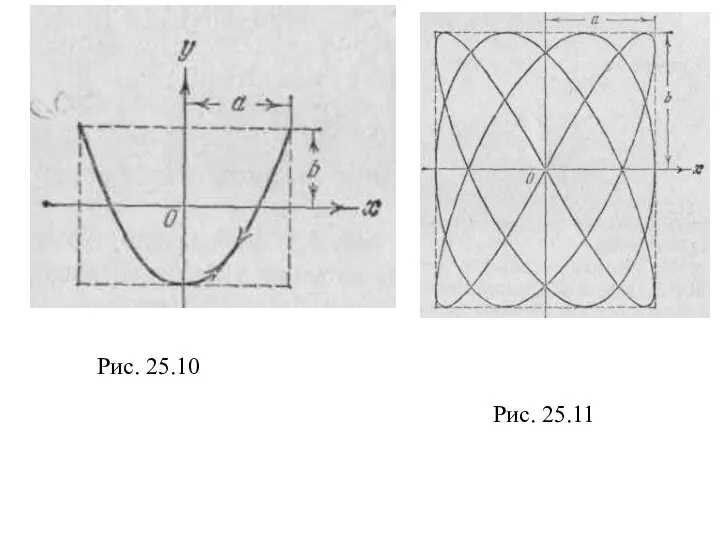
При отношении частот 1:2 и разности фаз, равной нулю, траектория вырождается в незамкнутую кривую (рис. 25.10), по которой точка движется туда и обратно. Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу. На рис. 25.11 для примера показана кривая для отношения частот 3:4 и разности фаз π/2.
довольно сложных кривых, называемых фигурами Лиссажу. На рис. 25.9 показана одна из простейших траекторий. Получающаяся при отношении частот 1:2 и разности фаз π/2. Уравнения колебаний имеют вид
х = аcosωt и y = bcos(2ωt+ π/2) (3.11)
За то время, пока вдоль оси х точка успевает пройти из одного крайнего положения в другое, вдоль оси у, выйдя из нулевого положения, она успевает достигнуть одного крайнего положения, затем другого и вернуться в нулевое положение.
При отношении частот 1:2 и разности фаз, равной нулю, траектория вырождается в незамкнутую кривую (рис. 25.10), по которой точка движется туда и обратно. Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу. На рис. 25.11 для примера показана кривая для отношения частот 3:4 и разности фаз π/2.
Слайд 8
Рис. 25.10
Рис. 25.11
Рис. 25.10
Рис. 25.11
Слайд 9
Рис. 25.125
Рис. 25.125
- Предыдущая
Сложение гармонических колебанийСледующая -
ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ





 Архитектура Владимиро-Суздальского княжества
Архитектура Владимиро-Суздальского княжества Черенков Фёдор Фёдорович
Черенков Фёдор Фёдорович Электроника. Последовательностная логика
Электроника. Последовательностная логика Презентация Характеристика элементов вывозных таможенных пошлин. Ставки и порядок их применения
Презентация Характеристика элементов вывозных таможенных пошлин. Ставки и порядок их применения Новая конституция РФ (приложение)
Новая конституция РФ (приложение) Всероссийский физкультурно-спортивный комплекс «Готов к труду и обороне» (ГТО): актуальные вопросы внедрения
Всероссийский физкультурно-спортивный комплекс «Готов к труду и обороне» (ГТО): актуальные вопросы внедрения Основы защиты информации в телекоммуникационных системах
Основы защиты информации в телекоммуникационных системах  Методика развития гибкости у детей 8-9 лет, занимающихся греко-римской борьбой
Методика развития гибкости у детей 8-9 лет, занимающихся греко-римской борьбой Программа элективного курса «Основы фитодизайна»
Программа элективного курса «Основы фитодизайна» Виды юридической ответственности
Виды юридической ответственности Мировая политика и мировая экономика в условиях глобализации
Мировая политика и мировая экономика в условиях глобализации Регрессия — погружение в прошлые жизни
Регрессия — погружение в прошлые жизни Эл пособие ч 2
Эл пособие ч 2 Характеристики и виды организаций
Характеристики и виды организаций Теорема Виета (8 класс) - презентация по Алгебре_
Теорема Виета (8 класс) - презентация по Алгебре_ Современная тактика лечения ОРЗ у часто болеющих детей
Современная тактика лечения ОРЗ у часто болеющих детей  Концепция производственной демократии
Концепция производственной демократии  E-commerce web 2.0 для Полякова Елена проектировщик интерфейсов HumanoIT Group. - презентация
E-commerce web 2.0 для Полякова Елена проектировщик интерфейсов HumanoIT Group. - презентация Posters NPE
Posters NPE Заповеди блаженств
Заповеди блаженств 격조사 (падежные частицы). Корейские окончания. Урок 2-4
격조사 (падежные частицы). Корейские окончания. Урок 2-4 Асинхронные двигатели
Асинхронные двигатели Приостановление сроков исковой давности
Приостановление сроков исковой давности Система команд МП I80X86. Команди пересилання даних, зсуви та арифметичні команди
Система команд МП I80X86. Команди пересилання даних, зсуви та арифметичні команди Профессия автомеханик
Профессия автомеханик НЕВРОЛОГИЯ Клещевой энцефалит
НЕВРОЛОГИЯ Клещевой энцефалит C# и Entity FrameWork
C# и Entity FrameWork Component Enabler for .NET
Component Enabler for .NET