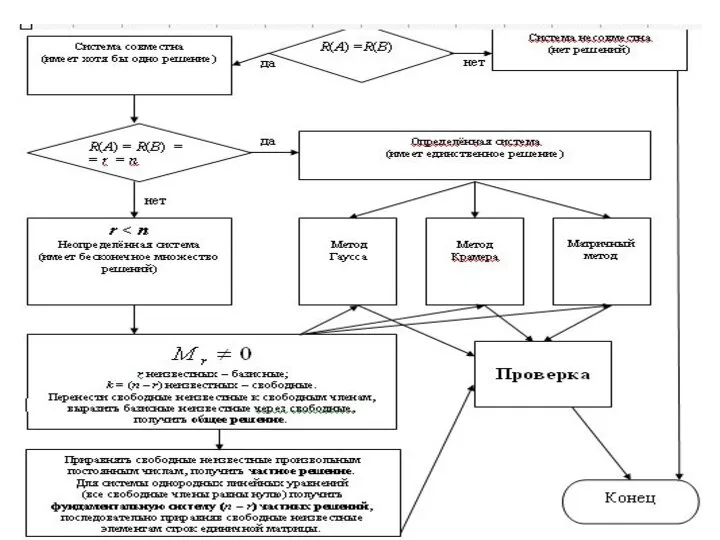
Содержание
- 2. 1. Общий вид, основные понятия, матричная форма Система m линейных уравнений с n неизвестными имеет вид:
- 3. Если , то СЛУ называется однородной. Если хотя бы один , то СЛУ называется неоднородной. Система,
- 4. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если имеет более одного решения.
- 5. Любую СЛУ можно представить в матричном виде: На основании согласованности матрицы А с матрицей Х: -
- 6. 2. Методы решения СЛУ Метод последовательного исключения неизвестных (Метод Гаусса) Метод Крамера (с помощью определителей) Метод
- 7. Метод последовательного исключения неизвестных (Метод Гаусса) Рассмотрим СЛУ: Данный метод применим к СЛУ любой размерности.
- 8. Алгоритм метода: 1 уравнение умножаем на и складываем со вторым уравнением системы; 1 уравнение умножаем на
- 9. 1 случай: В этом случае СЛУ имеет единственное решение. Значение находится из последнего уравнения, значение из
- 10. 2 случай: В этом случае СЛУ имеет бесконечно много решений. Из последнего уравнения выражается одно из
- 11. 3 случай: В этом случае СЛУ несовместна (не имеет решений), т.к. последнее уравнение является противоречивым. Замечание.
- 12. Метод Гаусса (метод исключения неизвестных) Две системы называются эквивалентными (равносильными), если их решения совпадают. К эквивалентной
- 13. Схема действий метода Гаусса: а) из всех уравнений системы кроме первого исключается неизвестное x1; б) из
- 14. Исключение неизвестных обычно осуществляют элементарными преобразованиями строк расширенной матрицы СЛУ. В результате расширенная матрица СЛУ приводится
- 15. Неизвестные, коэффициенты при которых вошли в базисный минор называются базисными неизвестными. Неизвестные, коэффициенты при которых не
- 16. Если n – число неизвестных системы, r – её ранг, то r неизвестных системы – базисные,
- 17. Если ранг основной и расширенной матриц СЛУ совпадает с числом неизвестных СЛУ, то свободных неизвестных нет.
- 18. Решение СЛУ, в котором базисные неизвестные выражены через свободные неизвестные, называется общим решением СЛУ. Решение, которое
- 19. Общее решение системы линейных уравнений можно получить, руководствуясь, например, следующим планом: а) выбрать базисный минор (обычно
- 20. Фундаментальной системой частных решений системы n однородных линейных уравнений (СОЛУ) называется система линейно независимых частных решений,
- 21. Фундаментальную систему частных решений (ФСЧР СОЛУ) получают обычно, последовательно приравнивая свободные неизвестные элементам строк единичной матрицы
- 22. 4. Метод Гаусса
- 23. Метод Гаусса (1)
- 24. Метод Гаусса (2) Рассмотрим систему
- 25. Метод Гаусса (3) Рассмотрим систему С помощью элементарных преобразований приводим ее к равносильной системе ступенчатого вида:
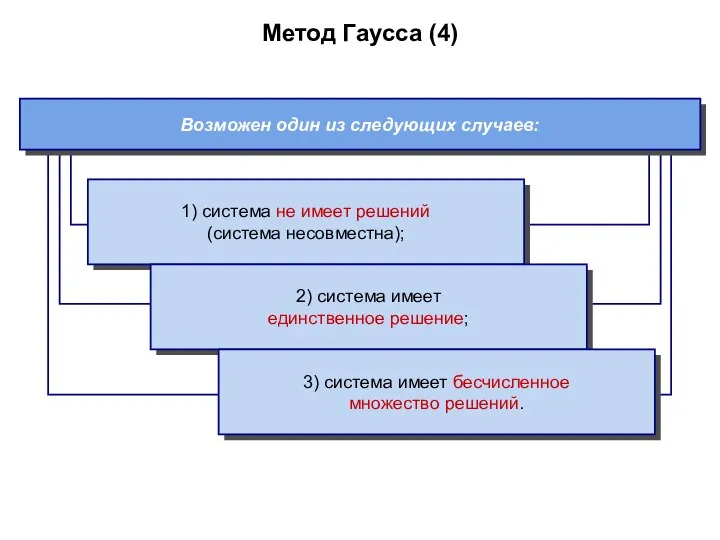
- 26. Метод Гаусса (4) Возможен один из следующих случаев: 1) система не имеет решений (система несовместна); 2)
- 27. Теорема Кронекера-Капелли (1) Рассмотрим систему уравнений
- 28. Теорема Кронекера-Капелли (2) Рассмотрим систему уравнений Обозначим
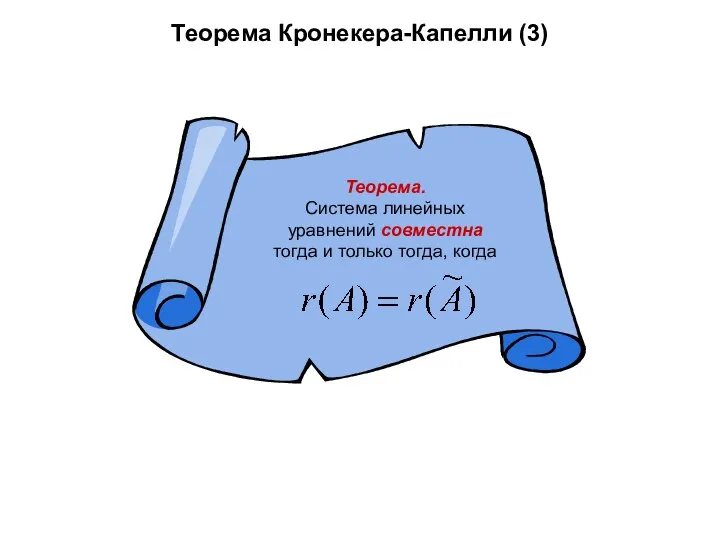
- 29. Теорема Кронекера-Капелли (3)
- 30. Пример 7 (1) Методом Гаусса решить систему уравнений:
- 31. Пример 7 (2) Решение. Запишем расширенную матрицу:
- 32. Пример 7 (3)
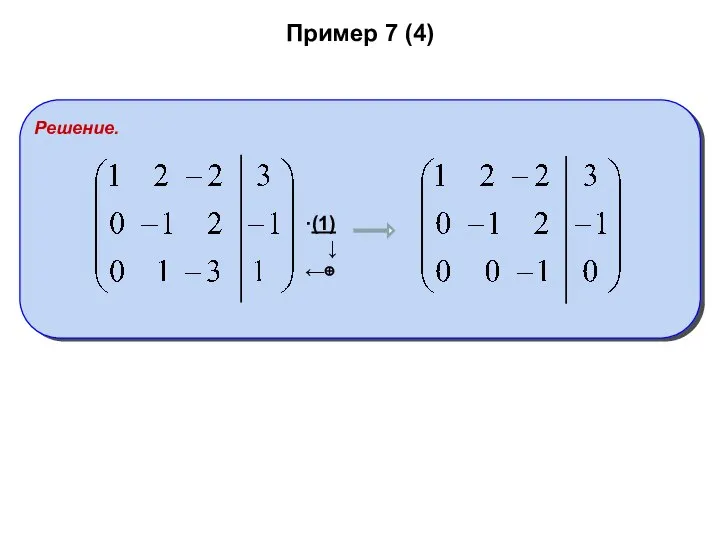
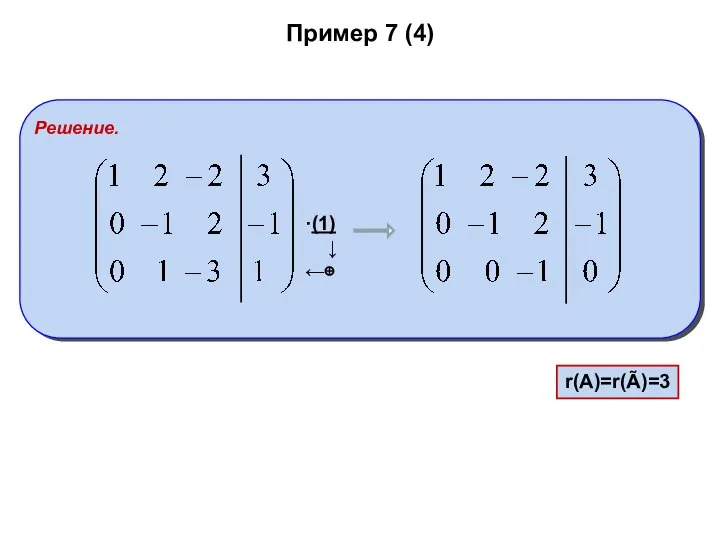
- 33. Пример 7 (4)
- 34. Пример 7 (4) r(A)=r(Ã)=3
- 35. Пример 7 (5) Решение.
- 36. Пример 7 (6) Решение.
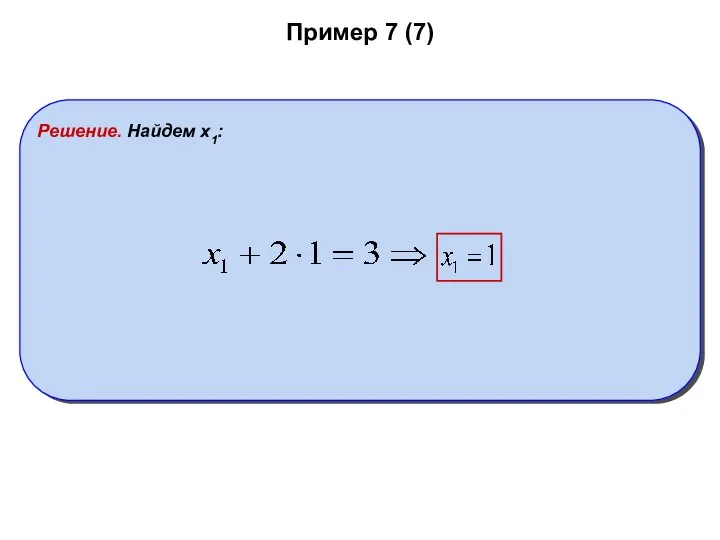
- 37. Пример 7 (7) Решение. Найдем x1:
- 38. Пример 7 (8) Решение. x1=1, x2=1, x3=0 – единственное решение.
- 39. 2) Метод Крамера Метод основан на вычислении определителей, поэтому применим к СЛУ размерности nxn. Рассмотрим СЛУ:
- 40. Введем следующие обозначения: Теорема. Если , то СЛУ имеет единственное решение , где . (Формулы Крамера)
- 41. 3) Метод обратной матрицы Метод основан на нахождении обратной матрицы, поэтому применим к СЛУ размерности nxn.
- 42. 3. Теорема Кронекера-Капелли Помимо метода Гаусса, на вопрос совместна ли СЛУ или нет можно воспользоваться теоремой
- 44. Системы линейных уравнений (1) Системой m линейных уравнений с n неизвестными называется система вида где aij
- 45. Пример 1
- 46. Пример 2
- 47. Пример 3
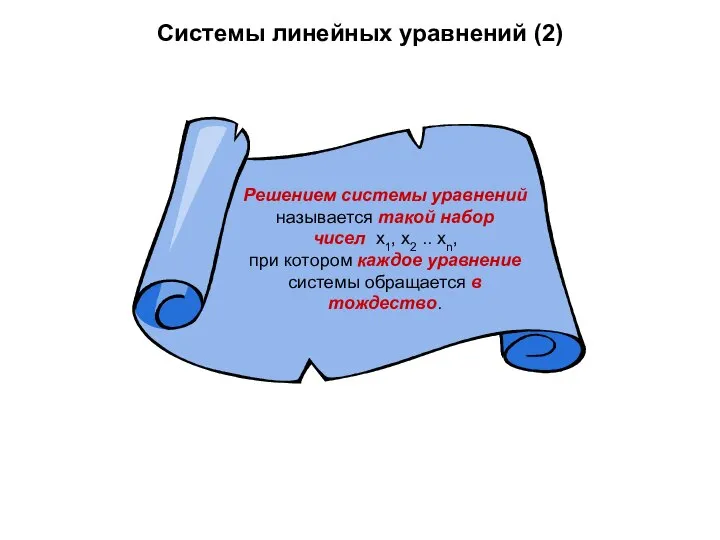
- 48. Системы линейных уравнений (2)
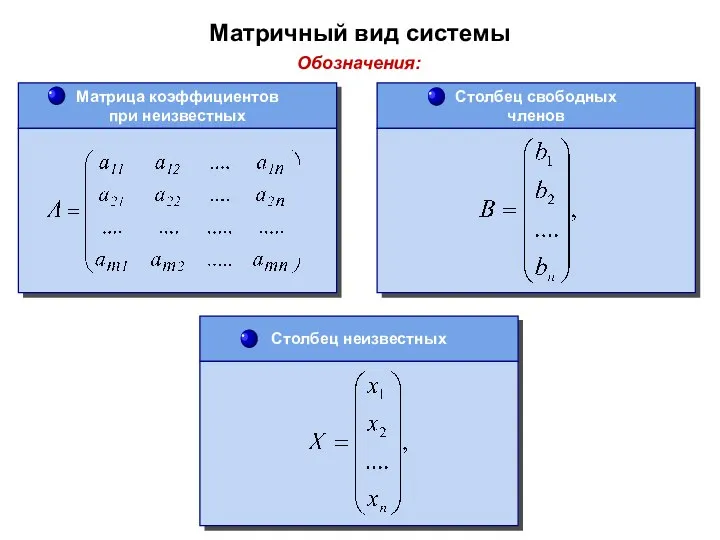
- 49. Матричный вид системы Обозначения: Матрица коэффициентов при неизвестных Столбец неизвестных Столбец свободных членов
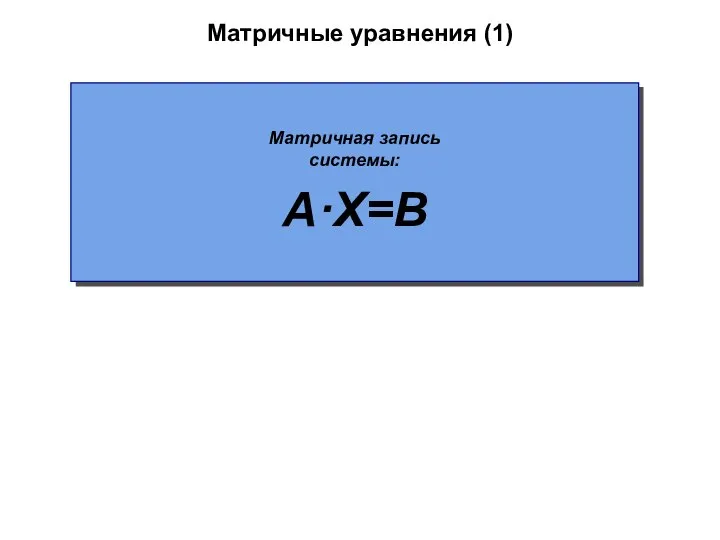
- 50. Матричные уравнения (1) Матричная запись системы: A·X=B
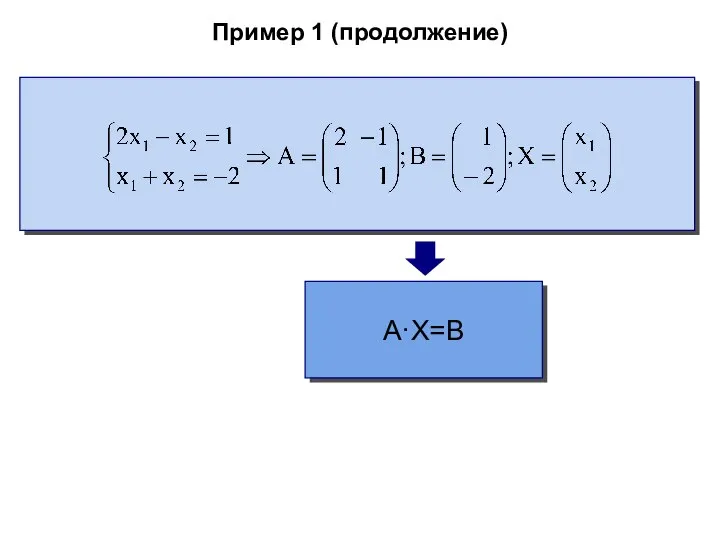
- 51. Пример 1 (продолжение) A·X=B
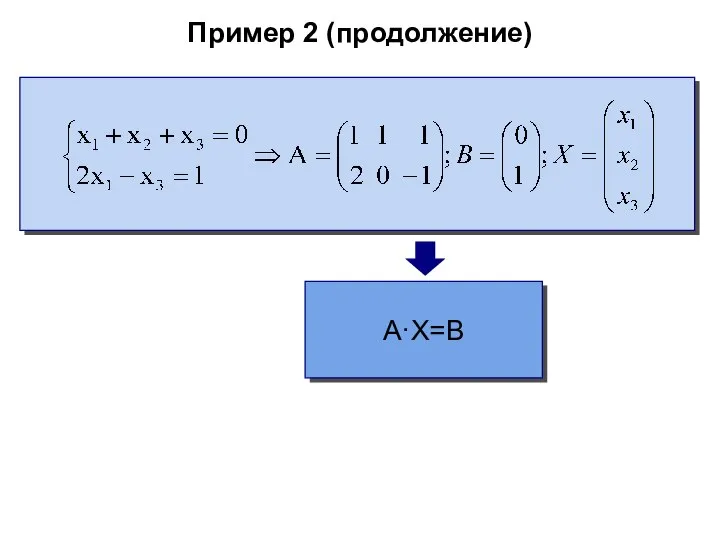
- 52. Пример 2 (продолжение) A·X=B
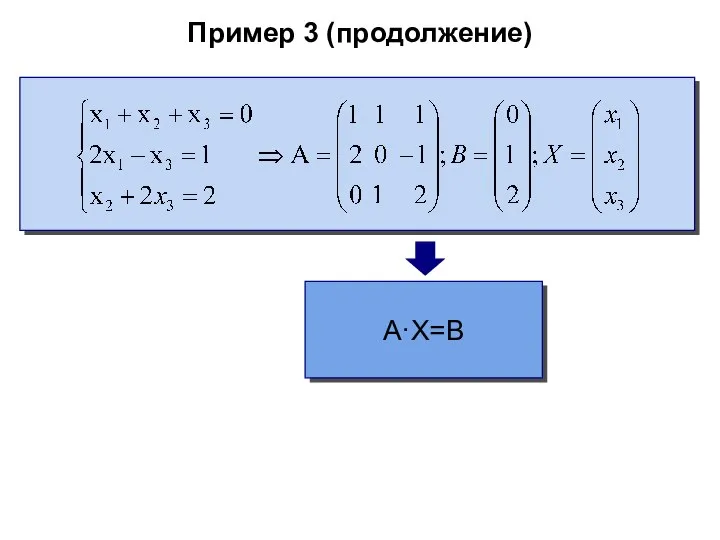
- 53. Пример 3 (продолжение) A·X=B
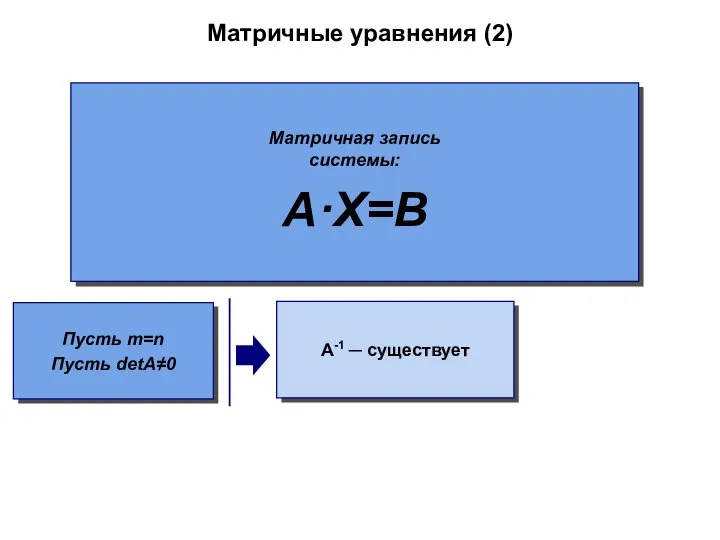
- 54. Матричные уравнения (2) Матричная запись системы: A·X=B A-1 ─ существует Пусть m=n Пусть detA≠0
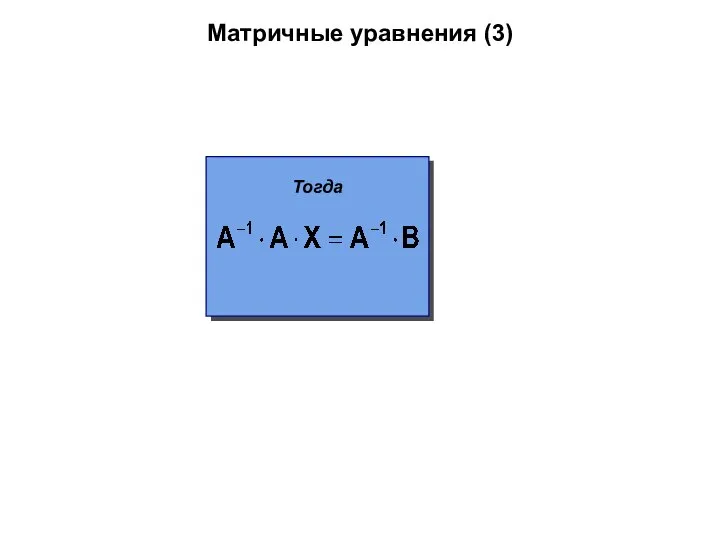
- 55. Матричные уравнения (3) Тогда
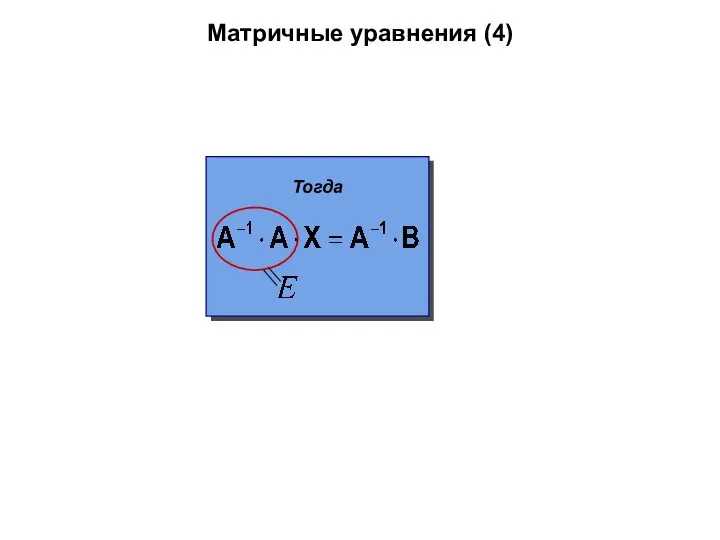
- 56. Матричные уравнения (4) Тогда
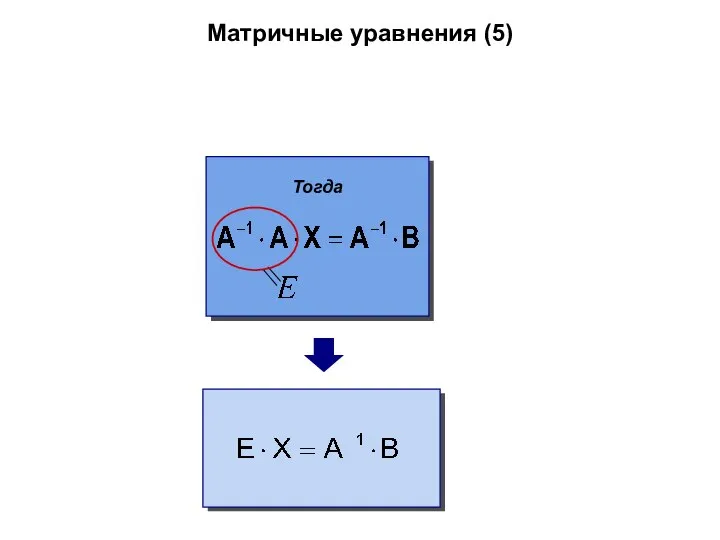
- 57. Матричные уравнения (5) Тогда
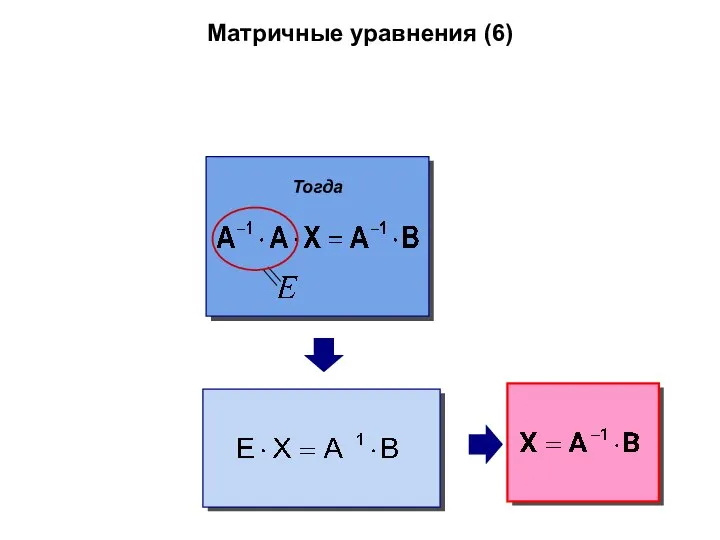
- 58. Матричные уравнения (6) Тогда
- 59. Пример 4 (1) Решите систему уравнений:
- 60. Пример 4 (2) Решите систему уравнений: Обозначим: Получим матричное уравнение: A·X=B Решение.
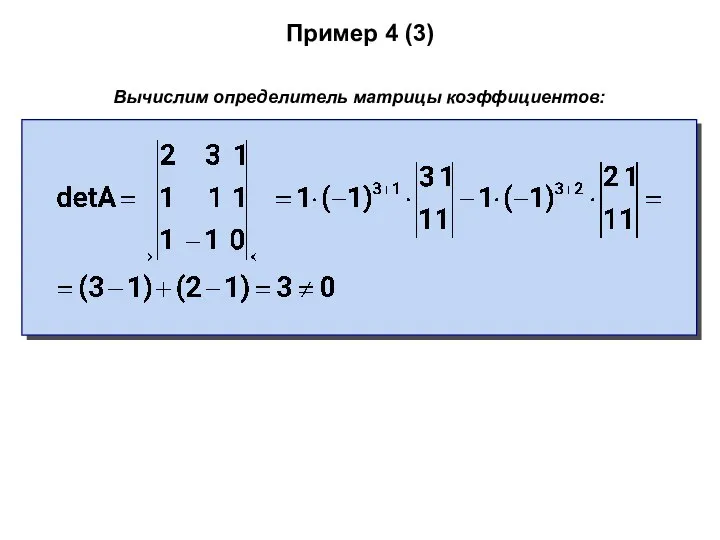
- 61. Пример 4 (3) Вычислим определитель матрицы коэффициентов:
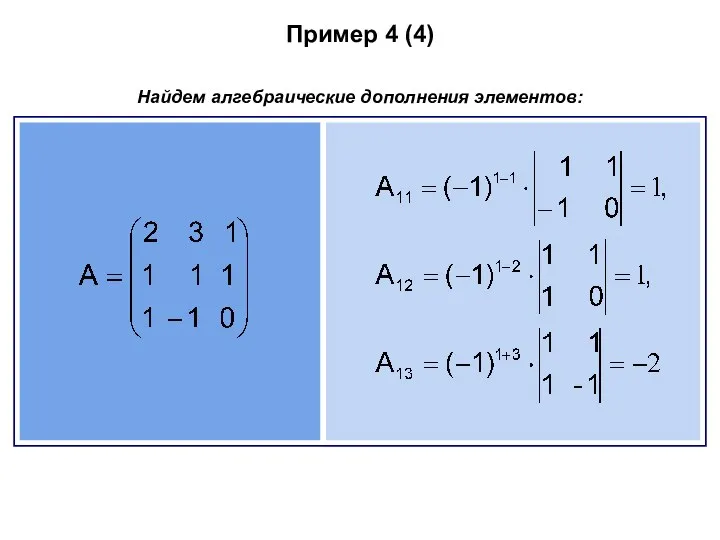
- 62. Пример 4 (4) Найдем алгебраические дополнения элементов:
- 63. Пример 4 (5)
- 64. Пример 4 (6)
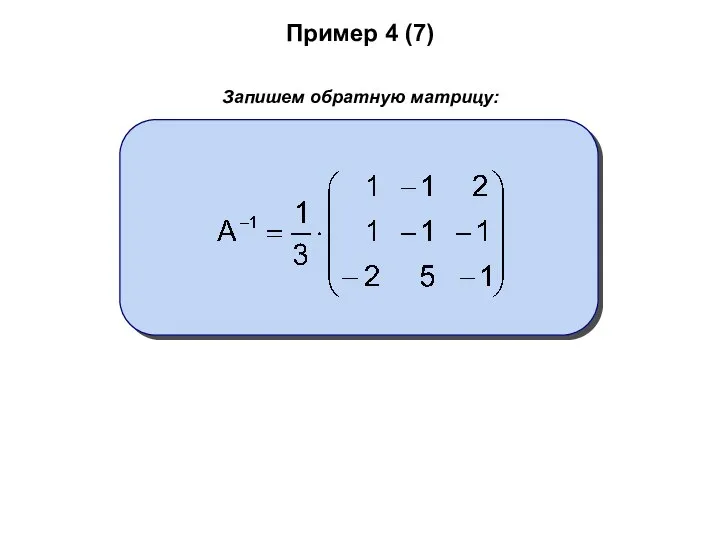
- 65. Пример 4 (7) Запишем обратную матрицу:
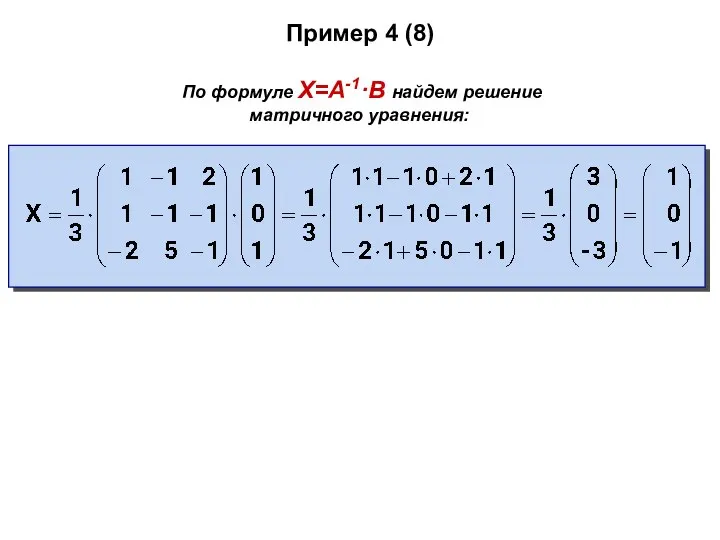
- 66. Пример 4 (8) По формуле X=A-1·B найдем решение матричного уравнения:
- 67. Правило Крамера (1) Пусть m=n Пусть detA = Δ ≠ 0 Рассмотрим систему
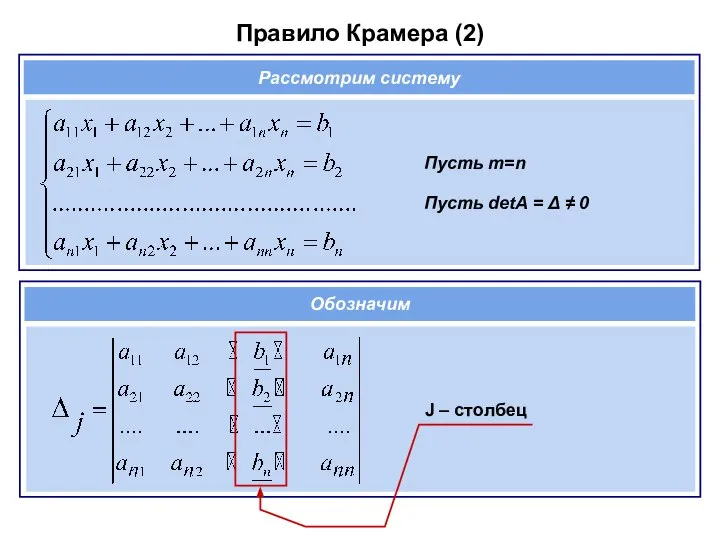
- 68. Правило Крамера (2) Пусть m=n Пусть detA = Δ ≠ 0 Рассмотрим систему J – столбец
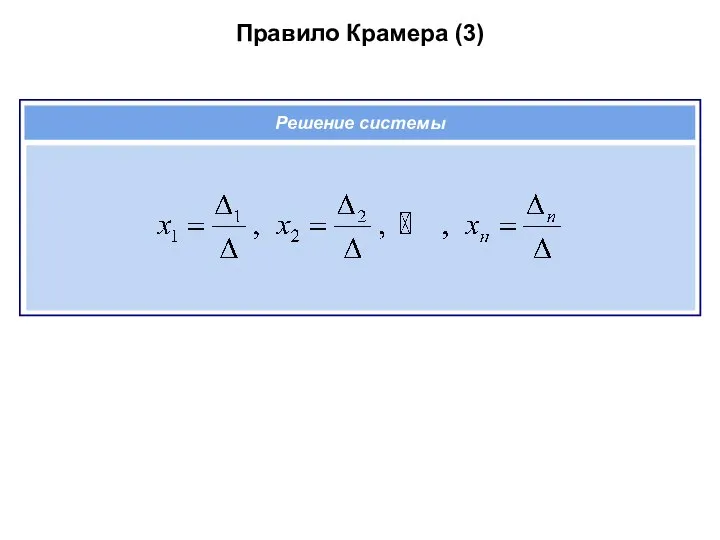
- 69. Правило Крамера (3) Решение системы
- 70. Пример 5 (1) Решите систему уравнений:
- 71. Пример 5 (2) Решение. Запишем определитель из коэффициентов уравнения: Решите систему уравнений:
- 72. Пример 5 (3) Решение. Запишем определитель из коэффициентов уравнения: Решите систему уравнений: Вычислим определители Δ1 и
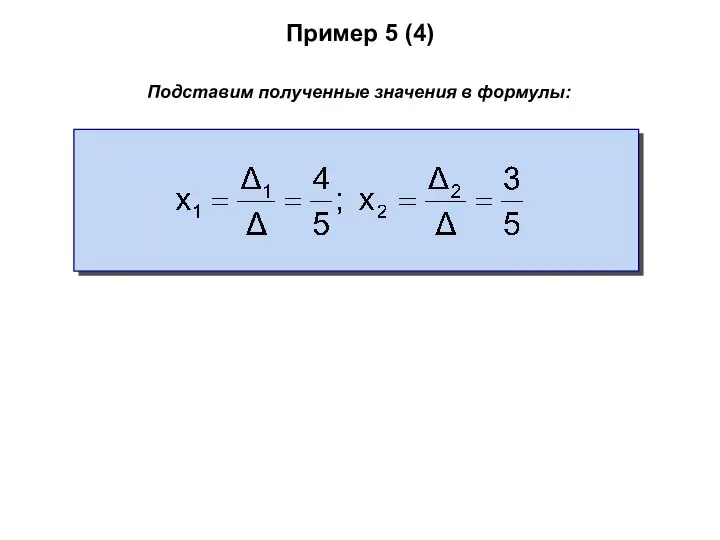
- 73. Пример 5 (4) Подставим полученные значения в формулы:
- 74. Занятие 5. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА.
- 75. Метод Гаусса – метод последовательного исключения переменных. Пусть задана система:
- 76. 1. Составим расширенную матрицу. 2. С помощью элементарных преобразований строк расширенную матрицу приведём к треугольному (ступенчатому)
- 77. Пример 6. Решить систему уравнений методом Гаусса:
- 78. Составим расширенную матрицу и приведём её к треугольному виду с помощью элементарных преобразований.
- 79. Получаем: Вернёмся к системе уравнений Ответ: х1=1; х2=2; х3=-2
- 80. Метод Гаусса применим к любой системе линейных уравнений. При этом система будет несовместной, т.е. не иметь
- 81. Решение: Составим расширенную матрицу и преобразуем её.
- 82. Получаем: Мы видим, что последнее уравнение будет 0 = 2. Значит, заданная система будет несовместной, т.е.
- 83. Пример 8. Решить систему: Решение: Составим расширенную матрицу и преобразуем её.
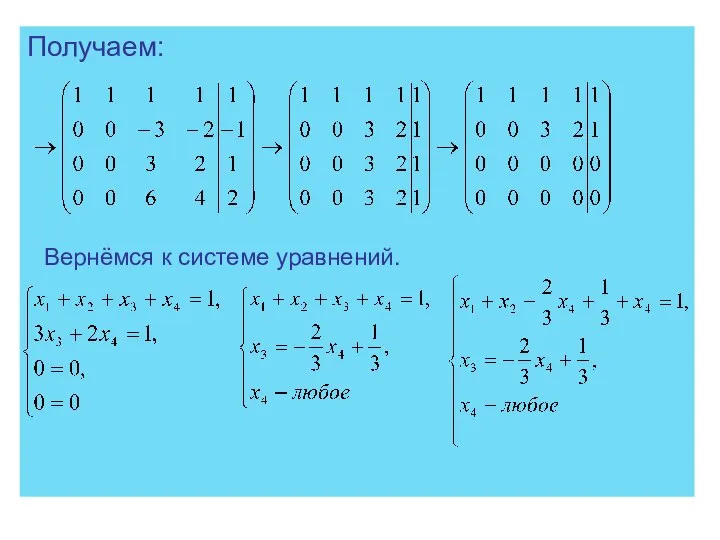
- 84. Получаем: Вернёмся к системе уравнений.
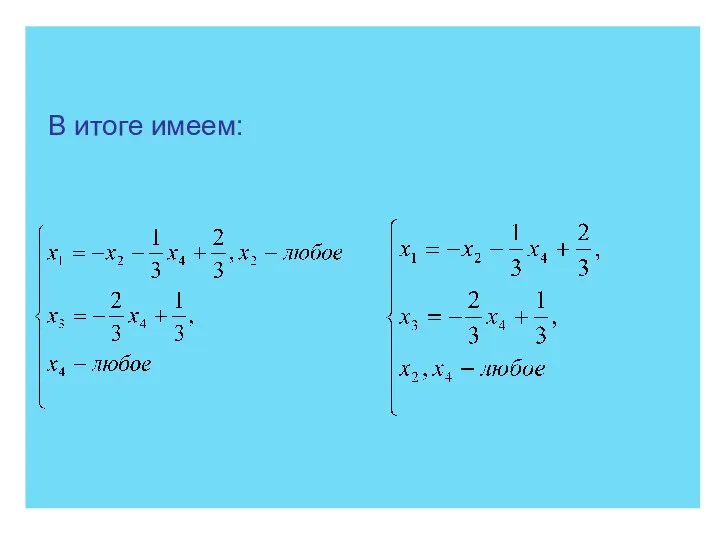
- 85. В итоге имеем:
- 86. Рассмотрим случай, когда заданная система состоит из линейных однородных уравнений, то есть уравнений, свободные члены которых
- 87. Решение: Эта система однородных уравнений; причём число уравнений меньше числа неизвестных (3 Составим матрицу из коэффициентов
- 88. Вернёмся к системе уравнений: Как мы видим, с помощью метода Гаусса можно решить любую систему, содержащую
- 89. Занятие 7 Решение систем линейных уравнений методом Крамера
- 90. Пусть дана система: Составим матрицу А из коэффициентов при неизвестных
- 91. Найдём определитель det A= Правило Крамера. Если m=n и det A≠0, то система совместна и имеет
- 92. Решение системы линейных уравнений : Находим определитель системы . Вычисляем определители х1, x2, … Возможны три
- 93. Пример 1. Решить систему: Решение:
- 94. Пример 2. Решить систему: Решение:
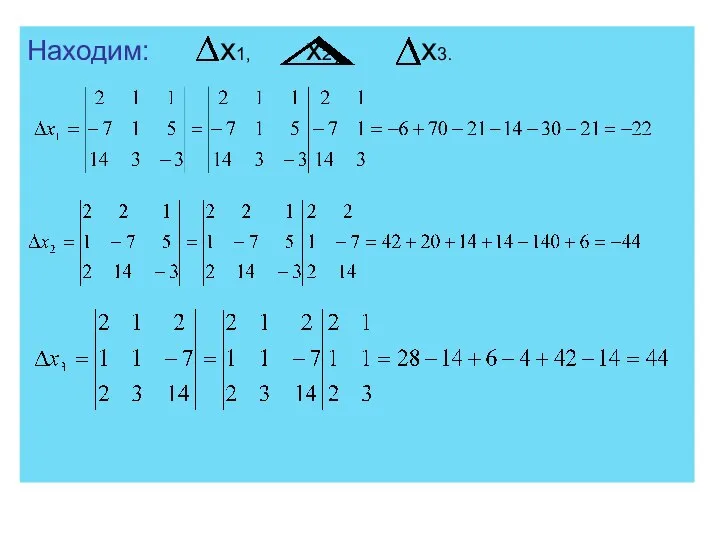
- 95. Находим: х1, х2, х3.
- 96. Применяем формулы Крамера: х1=1; х2=2; х3=-2
- 97. Занятие 9 РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ ОБРАТНОЙ МАТРИЦЫ
- 98. Дана система: Матричная запись системы линейных уравнений имеет вид: АХ=В Отсюда: Х= , где матрица, обратная
- 99. Пример 12. Решить с помощью обратной матрицы систему уравнений: Решение: Находим определитель Если = 0, то
- 100. Вычислим алгебраические дополнения для элементов каждой строки.
- 102. Скачать презентацию







































































 Механизм Отражения (Reflection) в C#
Механизм Отражения (Reflection) в C# Презентация на тему "Как правильно выбрать эффективный биологически активный препарат" - скачать презентации по Медицине
Презентация на тему "Как правильно выбрать эффективный биологически активный препарат" - скачать презентации по Медицине ТЕМА 5 БЕЗРАБОТИЦА В пользе безработицы больше всего уверены те, кто не знаком с ней по личному опыту. Джон Гелбрэйт, американски
ТЕМА 5 БЕЗРАБОТИЦА В пользе безработицы больше всего уверены те, кто не знаком с ней по личному опыту. Джон Гелбрэйт, американски Развития психики
Развития психики Рекурсия. Сортировка слиянием. Восходящая сортировка слиянием. Сложность сортировки. Устойчивость сортировок
Рекурсия. Сортировка слиянием. Восходящая сортировка слиянием. Сложность сортировки. Устойчивость сортировок Трансграничные туры социально-культурной направленности
Трансграничные туры социально-культурной направленности Нравственные основы службы в органах внутренних дел. Профессиональная этика сотрудника органов внутренних дел
Нравственные основы службы в органах внутренних дел. Профессиональная этика сотрудника органов внутренних дел Правовые основы охраны труда
Правовые основы охраны труда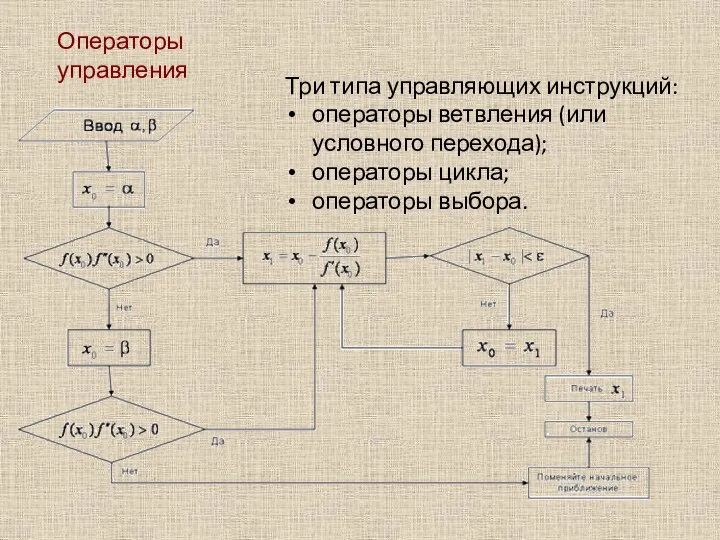 Операторы управления
Операторы управления Презентация Цена и общая стоимость контракта Виды цен Определение валюты цены
Презентация Цена и общая стоимость контракта Виды цен Определение валюты цены 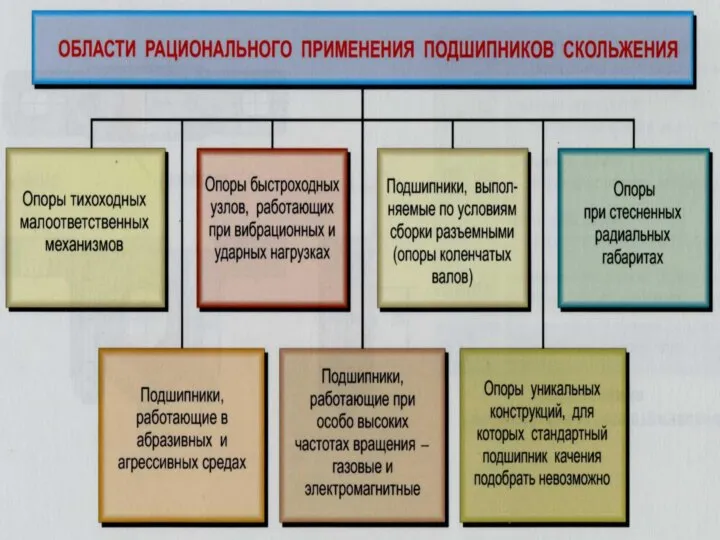 Области рационального применения подшипников скольжения
Области рационального применения подшипников скольжения Презентация Законы и иные источники ПСО. Их роль
Презентация Законы и иные источники ПСО. Их роль Litania Loretańska
Litania Loretańska Языки программирования
Языки программирования Методология научных исследований
Методология научных исследований Проблемно-контрольные вопросы Что такое институт права. Какие признаки присущи правовому институту? Что представляют собой
Проблемно-контрольные вопросы Что такое институт права. Какие признаки присущи правовому институту? Что представляют собой  НАЛОГОВЫЙ КОДЕКС: для транспортных предприятий
НАЛОГОВЫЙ КОДЕКС: для транспортных предприятий  Презентация Microsoft Office PowerPoint
Презентация Microsoft Office PowerPoint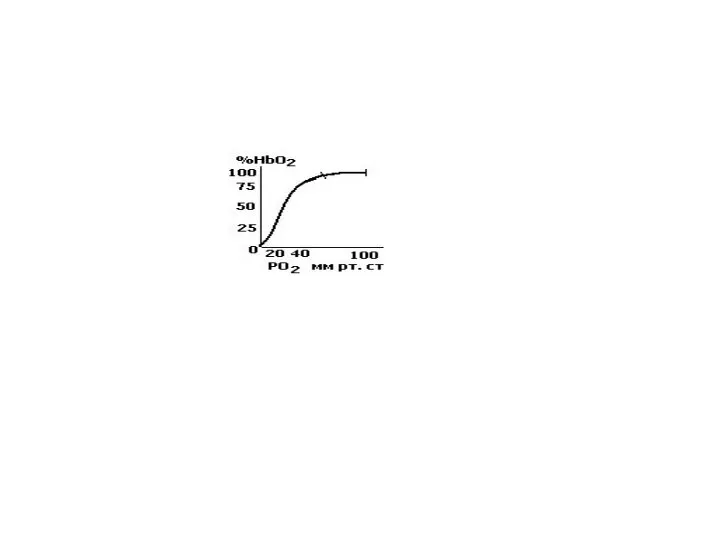 дыхание 2
дыхание 2 Устройство пк
Устройство пк  Аттестация как элемент планирования карьеры
Аттестация как элемент планирования карьеры Субиндексы степени развития бизнеса Нечаева Анастасия, Юрлова Виктория, МЭ-102
Субиндексы степени развития бизнеса Нечаева Анастасия, Юрлова Виктория, МЭ-102 Тензор поляризуемости диэлектрика
Тензор поляризуемости диэлектрика
 Регистры x86-64. Компьютерные основы программирования. Представление программ, часть 4
Регистры x86-64. Компьютерные основы программирования. Представление программ, часть 4 Инфляция «Инфляция — одна из форм налогообложения, не нуждающаяся в законодательном одобрении». Лауреат Нобелевской премии по
Инфляция «Инфляция — одна из форм налогообложения, не нуждающаяся в законодательном одобрении». Лауреат Нобелевской премии по Мужская парфюмерия
Мужская парфюмерия Политическая система
Политическая система Понятие и виды правомерного поведения
Понятие и виды правомерного поведения