Содержание
- 2. ЛЕКЦИЯ 3 «ВЕСА ИЗМЕРЕНИЙ И ИХ ФУНКЦИЙ. ОБРАБОТКА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ».
- 3. 1. Веса измерений и их свойства. Соотношение между весами и средними квадратическими ошибками. Вес среднего арифметического.
- 4. 5.Поправки неравноточных измерений одной и той же величины и их свойства. Оценка точности неравноточных измерений и
- 5. 1.Веса измерений и их свойства. Соотношение между весами и средними квадратическими ошибками. Вес среднего арифметического. При
- 6. Вес измерения р – величина обратно-пропорциональная квадрату средней квадратической ошибки этого измерения: (1) В этой формуле
- 7. Поскольку k выбирается произвольно, при решении данной задачи все веса можно увеличивать или уменьшать в одно
- 8. т.е. веса двух измерений обратно пропорциональны квадратам их средних квадратических ошибок. Это второе свойство весов. Отсюда
- 9. Найдем вес среднего арифметического, принимая вес р отдельного измерения равным единице. Обозначим вес среднего арифметического через
- 10. Подставляя р =1 и Р = п, (3) , получим т.е. вес среднего арифметического равен числу
- 11. На этом основании любой результат измерений c весом p можно понимать как среднее арифметическое из ряда
- 12. 2. Веса функций измеренных величин. Ранее были выведены формулы для нахождения СКО функций. Веса и СКО
- 13. Принимая k=1, получим Величину называют обратным весом.
- 14. Если в ранее выведенные формулы подставить вместо квадратов СКО соответствующие обратные веса, то получим формулы для
- 15. 2. (5)
- 16. 3. (6)
- 17. 4. (7)
- 18. Если измерения равноточные, то откуда т.е. вес суммы n равноточных слагаемых в n раз меньше веса
- 19. 5. u = f (x1, x2, …, xn), (9)
- 20. 3. Средняя квадратическая ошибка единицы веса. Средней квадратической ошибкой единицы веса μ называют СКО измерения, вес
- 21. Выразим μ через истинные ошибки Δ. Пусть измерению с весом p соответствует СКО m. На основании
- 22. Откуда (10) (11) (12)
- 23. Пусть имеется ряд измерений l1, l2, …, ln, с весами p1, p2, …, pn. Составим вспомога-тельные
- 24. Для равноточных измерений можно записать или (13)
- 25. 4. Среднее весовое. Средняя квадратическая ошибка и вес среднего весового. Рассмотрим обработку результатов неравноточных измерений одной
- 26. Результат любого измерения li можно рассматривать как среднее арифметическое из pi воображаемых измерений каждое с весом
- 27. Таким образом, измерения можно свести к равноточным и окончательное значение вычислить по формуле среднего арифме- тического
- 28. Из (14) следует, что Подставляя в (15), получим (16)
- 29. Величину LB называют средним весовым значением (весовым средним, средневзве- шенным, общей арифметической срединой). Для упрощения расчетов
- 30. Величина [p] – сумма весов, а следовательно, общее число измерений с весом единица, из которых получено
- 31. В результате получим или (19)
- 32. 5. Поправки неравноточных измерений одной и той же величины и их свойства. Оценка точности неравноточных измерений
- 33. Запишем поправки для всех n измерений, умножим на соответствующие веса и сложим [pv] = LB [p]
- 34. Подставляя [pv] = 0. (21) Это первое свойство поправок неравноточных измерений. Равенство (21) контролирует правильность вычисления
- 35. Второе свойство поправок для неравноточных измерений одной и той же величины выражается равенством [pv2] = min.
- 36. Вычисления контролируются по формуле [p v2] = – [pvl] = – [pvε]. Если LB округлено, то
- 37. 6. Определение средней квадратической ошибки единицы веса по разностям двойных неравноточных измерений. Пусть при двойном измерении
- 38. Составим разности d1 = l1 – l1/, d2 = l2 – l2/, …. …. … …
- 39. Каждая разность di = li – li/ является функцией равноточных измерений с весом pi. Следовательно, При
- 40. После исключения систематических ошибок СКО единицы веса находят по формуле (28)
- 41. 7. Оценка точности измерения углов и превышений по невязкам в полигонах и ходах Во всех замкнутых
- 42. Если вес измерения одного угла принять равным единице, то вес суммы n углов найдется по формуле
- 43. Здесь μ является СКО измерения одного угла, т.к. за единицу веса принят вес одного угла. Поэтому
- 44. Для триангуляции n =3, поэтому Для четырехугольников (32) (31)
- 45. Аналогичными рассуждениями можно получить формулу для оценки точности превышений геометрического нивелирования. Если сумме превышений на 1
- 46. СКО единицы веса (СКО в сумме превышений на 1 км хода) найдется по формуле где fh
- 47. В качестве единицы веса можно взять вес превышения на одной станции. Тогда вес суммы превышений из
- 49. Скачать презентацию












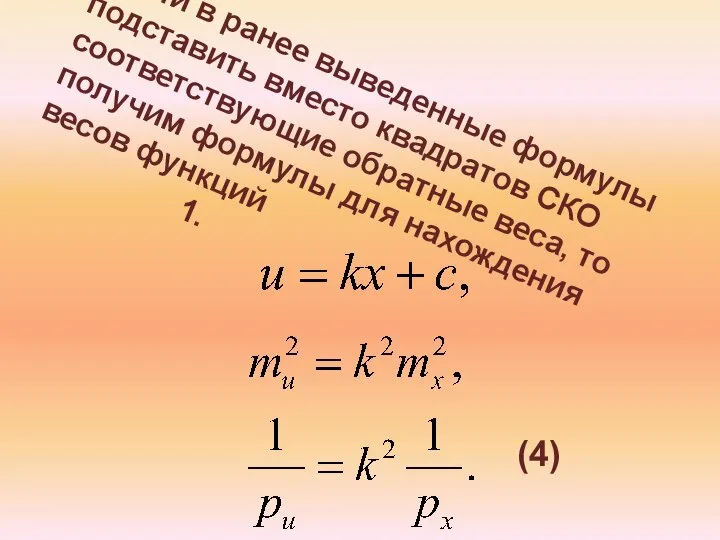
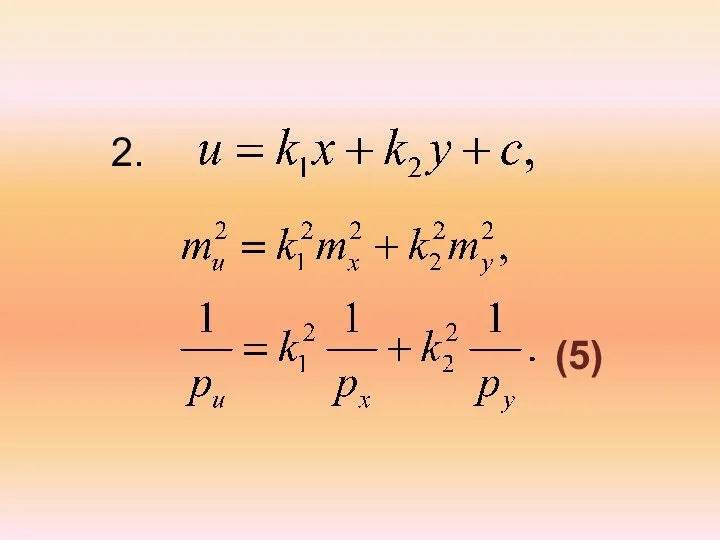
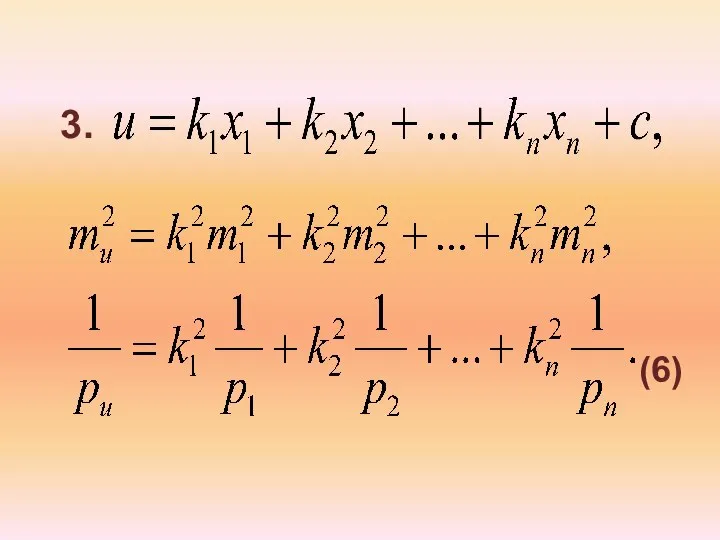
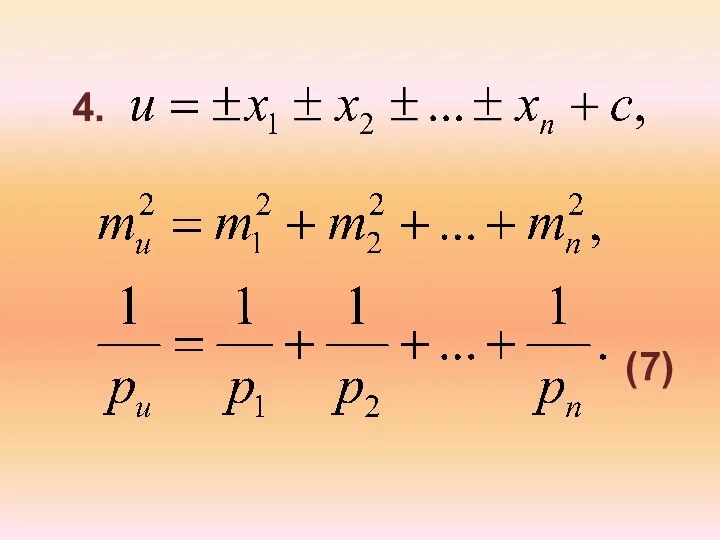

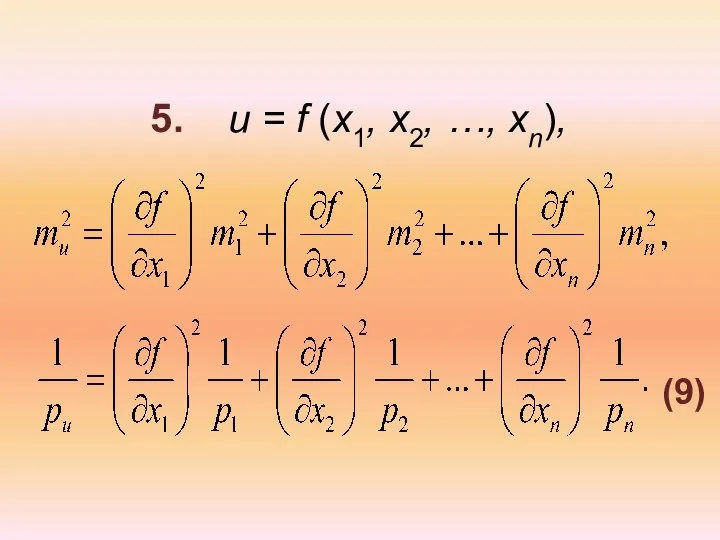










![Величина [p] – сумма весов, а следовательно, общее число измерений с](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1304991/slide-29.jpg)



![Подставляя [pv] = 0. (21) Это первое свойство поправок неравноточных измерений.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1304991/slide-33.jpg)

![Вычисления контролируются по формуле [p v2] = – [pvl] = –](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1304991/slide-35.jpg)











 САВЕЗ САМОСТАЛНИХ СИНДИКАТА ГРАДА НОВОГ САДА И ОПШТИНА. - презентация
САВЕЗ САМОСТАЛНИХ СИНДИКАТА ГРАДА НОВОГ САДА И ОПШТИНА. - презентация Индексы
Индексы Социальная поддержка семей, имеющих детей
Социальная поддержка семей, имеющих детей  Презентация Разрешительный порядок вывоза культурных ценностей из Российской Федерации
Презентация Разрешительный порядок вывоза культурных ценностей из Российской Федерации Весна
Весна Сборка компьютера
Сборка компьютера Взаимосвязь функций управления
Взаимосвязь функций управления Структура и содержание физической подготовки девушек – спринтеров 18-19 лет в годичном цикле тренировки
Структура и содержание физической подготовки девушек – спринтеров 18-19 лет в годичном цикле тренировки profit and loss account
profit and loss account Жилой комплекс «Васильевский квартал»
Жилой комплекс «Васильевский квартал» Факторы развития одаренности Корчуганова Ирина Павловна, доцент, кандидат психологических наук 26.04.2011
Факторы развития одаренности Корчуганова Ирина Павловна, доцент, кандидат психологических наук 26.04.2011 Анатомия человека
Анатомия человека Centrum logistyczne
Centrum logistyczne Презентация на тему "Совместная деятельность с детьми средней группы по формированию правил дорожного движения и поведения на
Презентация на тему "Совместная деятельность с детьми средней группы по формированию правил дорожного движения и поведения на  Окружающий мир 3класс Тема «Разнообразие растений» Учитель начальных классов Шеремет Н.Д. МБОУ «СОШ № 37» г. Симферополь Респ
Окружающий мир 3класс Тема «Разнообразие растений» Учитель начальных классов Шеремет Н.Д. МБОУ «СОШ № 37» г. Симферополь Респ Освоение космоса
Освоение космоса Биохимические закономерности адаптации к мышечной работе
Биохимические закономерности адаптации к мышечной работе Вяжущие вещества. Виды
Вяжущие вещества. Виды Самый вкусный и ароматный бизнес
Самый вкусный и ароматный бизнес Контроль со стороны профсоюзов за соблюдением законодательства по охране труда в организациях Свердловской области
Контроль со стороны профсоюзов за соблюдением законодательства по охране труда в организациях Свердловской области Международное сотр в УС
Международное сотр в УС Подготовка к ЕГЭ 2014 по математике Решение задания С1
Подготовка к ЕГЭ 2014 по математике Решение задания С1 Давид Самойлов Белые стихи
Давид Самойлов Белые стихи Интегрированный банк данных «ИБД-Регион»
Интегрированный банк данных «ИБД-Регион» Будова української хати
Будова української хати Массивы (Turbo Pascal)
Массивы (Turbo Pascal) Маркетинговые исследования
Маркетинговые исследования Презентация Анализ экономического потенциала Восточной зоны РФ
Презентация Анализ экономического потенциала Восточной зоны РФ