Содержание
- 2. 2. Кинематика. Векторный способ задания движения точки. Положение точки М задается ее радиусом-вектором , проведенным из
- 3. 3. Кинематика. Координатный способ задания движения точки. Положение точки можно задать ее координатами x, y, z,
- 4. 4. Кинематика. Естественный способ задания движения. Траектория точки М – кривая АВ – известна (рис.38). Точку
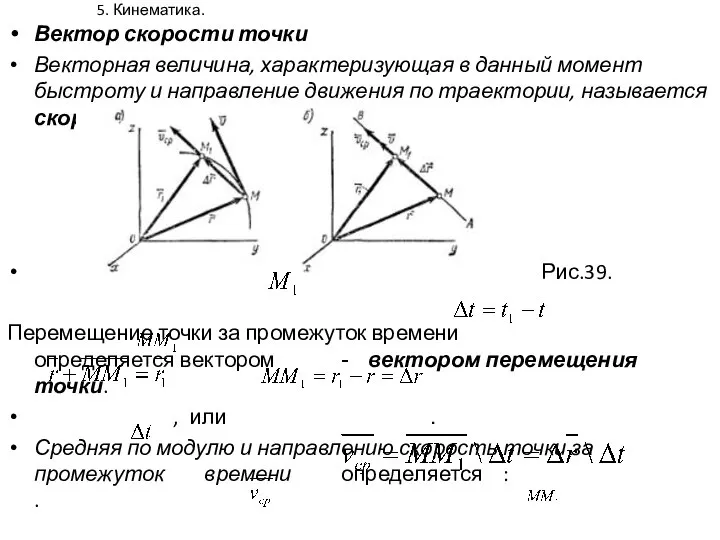
- 5. 5. Кинематика. Вектор скорости точки Векторная величина, характеризующая в данный момент быстроту и направление движения по
- 6. 6. Кинематика. Вектор скорости точки. Если промежутки времени малы ( 0) средняя скорость становится равной истинной
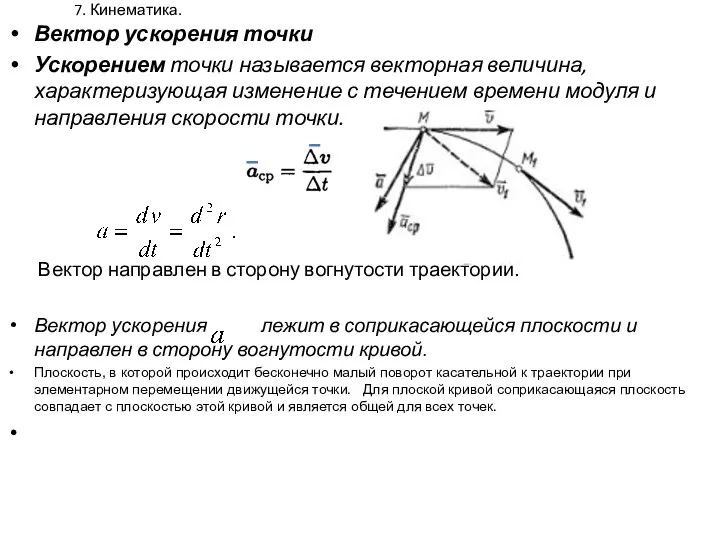
- 7. 7. Кинематика. Вектор ускорения точки Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля
- 8. 8. Кинематика. Скорость и ускорение точки при координатном способе задания движения Воспользуемся теоремой: проекция производной от
- 9. 9. Кинематика. 2. Ускорение точки. Вектор ускорения: Отсюда: , , , или , , . Проекции
- 10. 10. Кинематика. Скорость и ускорение точки при естественном задания движения Даны траектория точки и закон движения
- 11. 11. Кинематика. Скорость и ускорение точки при естественном задании движения. Поскольку вектор скорости точки совпадает с
- 12. 12. Кинематика. Касательное и нормальное ускорение точки Проекции вектора на оси , Mn, Mb: , ,
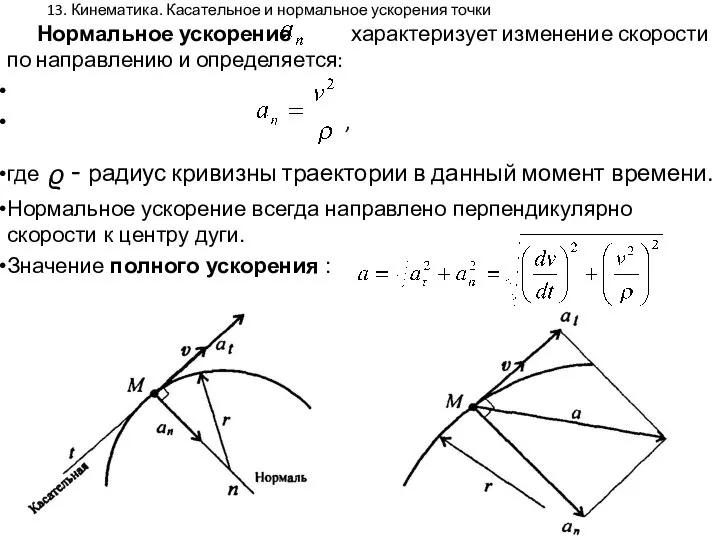
- 13. 13. Кинематика. Касательное и нормальное ускорения точки Нормальное ускорение характеризует изменение скорости по направлению и определяется:
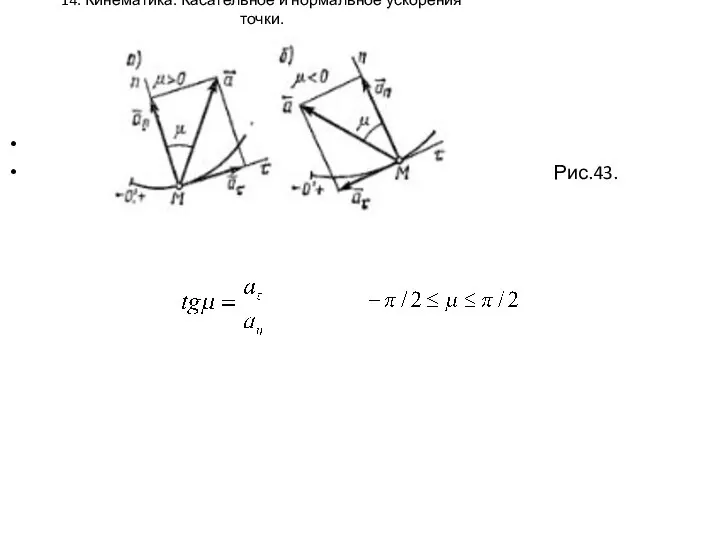
- 14. 14. Кинематика. Касательное и нормальное ускорения точки. Рис.43.
- 15. 15. Кинематика. Частные случаи движения точки. 1. Прямолинейное движение. , , . Касательное ускорение характеризует изменение
- 16. 16. Кинематика. Частные случаи движения точки. 3. Равномерное прямолинейное движение. , . Ускорение точки равно нулю
- 17. 17. Кинематика. Поступательное движение. Кинематика твердого тела Поступательное движение Поступательным называется такое движение твердого тела, при
- 18. 18. Кинематика. Поступательное движение Поскольку поступательное движение твердого тела определяется движением какой-либо его точки, его движение
- 19. 19. Кинематика. Вращательное движение твердого тела вокруг неподвижной оси. Если твердое тело движется так, что две
- 20. 20. Кинематика. Вращательное движение. Угловая скорость тела определяется: или . Таким образом, числовое значение угловой скорости
- 21. 21. Кинематика. Равномерное вращение Угловая скорость постоянна, т.е. = const . - закон равном. кривол. дв-я
- 22. 22. Кинематика. Определение скоростей и ускорений точек вращающегося тела 1. Скорость точек тела Рис.50. Рис. 51.
- 23. 23. Кинематика. Скорость точек твердого тела при вращательном движении. Скорость точки v называют линейной или окружной
- 24. 24. кинематика. Вращательное движение твердого тела. 2.Ускорение точек тела. Воспользуемся формулами: , , . Тогда, ,
- 25. 25. Кинематика. Ускорение точек тела. Рис.53. Рис.54. Отклонение вектора полного ускорения от радиуса описываемой точкой окружности
- 26. 28. Кинематика. Плоскопараллельное движение. Плоскопараллельное движение твердого тела Плоскопараллельным движением твердого тела называется такое, при котором
- 27. 29. Кинематика. Плоскопараллельное движение твердого тела. На плоскости сечения S проведем отрезок АВ, который и будет
- 28. 30. Кинематика. Плоскопараллельное движение. Основные кинематические характеристики этого движения являются: 1) скорость и ускорение поступательного движения,
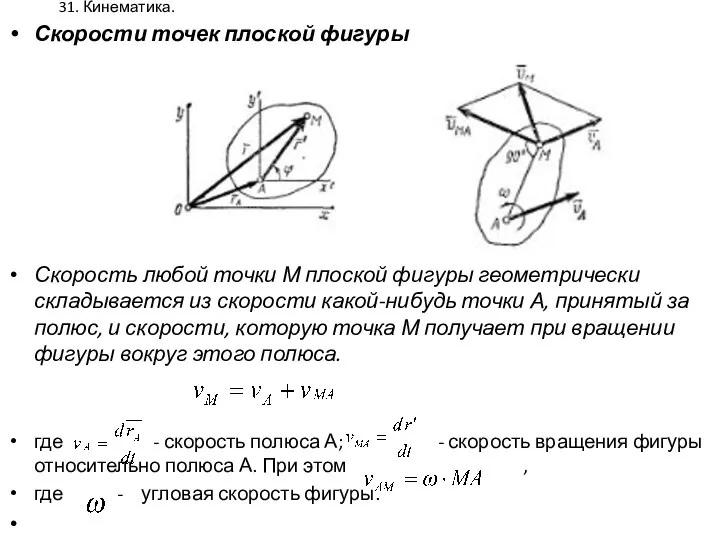
- 29. 31. Кинематика. Скорости точек плоской фигуры Скорость любой точки М плоской фигуры геометрически складывается из скорости
- 30. 32. Кинематика. Ускорение точек плоской фигуры Ускорение каждой точки движущейся плоской фигуры равно геометрической сумме двух
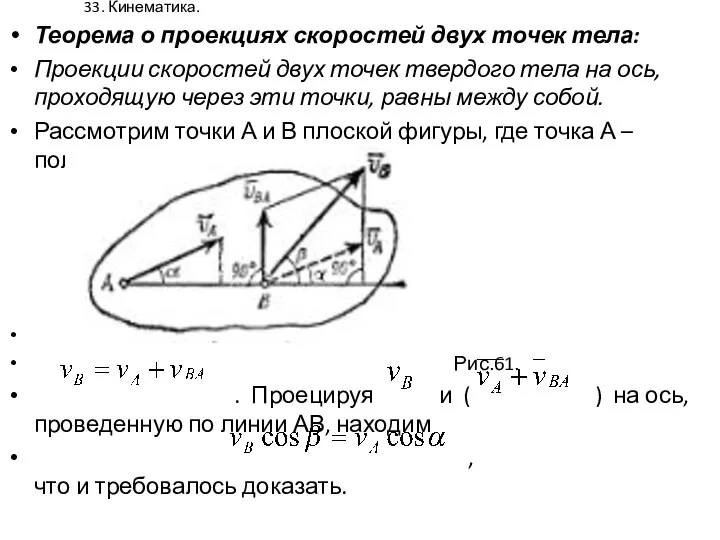
- 31. 33. Кинематика. Теорема о проекциях скоростей двух точек тела: Проекции скоростей двух точек твердого тела на
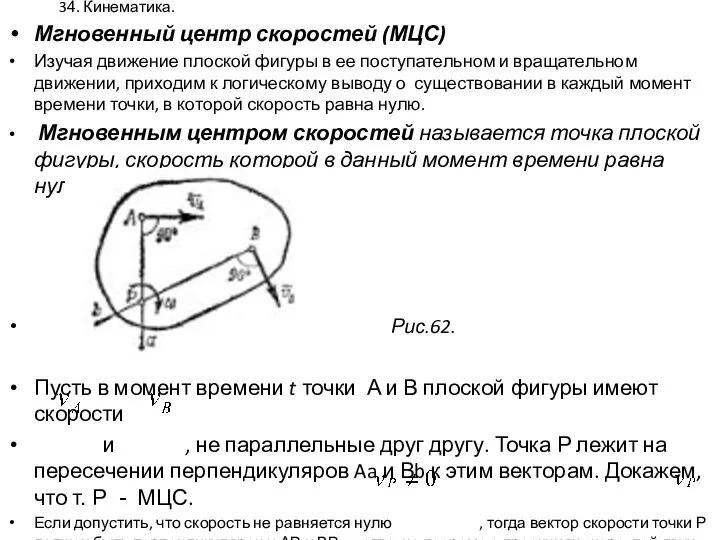
- 32. 34. Кинематика. Мгновенный центр скоростей (МЦС) Изучая движение плоской фигуры в ее поступательном и вращательном движении,
- 33. 35. Кинематика. МЦС. Если Р - полюс, то скорость, например, точки А в момент времени t:
- 34. 36. Кинематика. МЦС. Выводы: 1. Для определения МЦС надо знать только направления скоростей и двух точек
- 35. 37. Кинематика. Частные случаи определения МЦС: 1. При качении без скольжения одного цилиндрического тела по поверхности
- 37. Скачать презентацию



























 Классификация нелинейных элементов и цепей
Классификация нелинейных элементов и цепей Физика атомного ядра
Физика атомного ядра Презентация по физике Магнитные свойства вещества Диамагнетики, парамагнетики, ферромагнетики
Презентация по физике Магнитные свойства вещества Диамагнетики, парамагнетики, ферромагнетики  ПИД - регулятор
ПИД - регулятор Наноматериалы и нанотехнологии. Галогенидосеребряные светочувствительные материалы
Наноматериалы и нанотехнологии. Галогенидосеребряные светочувствительные материалы Термодинамика. Основные понятия и определения. Теплота и работа, как форма передачи энергии
Термодинамика. Основные понятия и определения. Теплота и работа, как форма передачи энергии Методы исследования нанообъектов и нанокомпозитов
Методы исследования нанообъектов и нанокомпозитов Сила. Явление тяготения. Сила тяжести
Сила. Явление тяготения. Сила тяжести Предмет физической химии
Предмет физической химии Фізіка вакол нас
Фізіка вакол нас Получение изображения при помощи линзы. Лабораторная работа № 11
Получение изображения при помощи линзы. Лабораторная работа № 11 Физические велечины. Задания
Физические велечины. Задания Работа электрического тока
Работа электрического тока Основы теории пограничного слоя
Основы теории пограничного слоя Современные представления о структурных уровнях и формах окружающего мира
Современные представления о структурных уровнях и формах окружающего мира Механічні взаємодії. Сила. Вимірювання сил. Рівнодійна
Механічні взаємодії. Сила. Вимірювання сил. Рівнодійна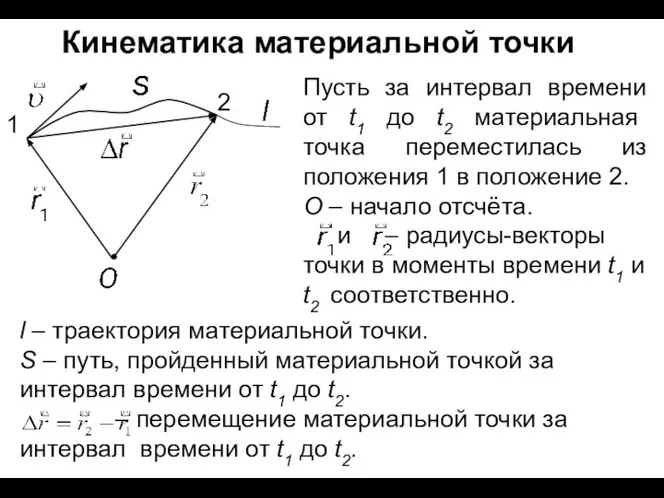 Кинематика материальной точки
Кинематика материальной точки Решение задач на применение законов Ньютона
Решение задач на применение законов Ньютона Синхронные генераторы трехфазного переменного тока
Синхронные генераторы трехфазного переменного тока Кинематика вращательного движения. Поступательное движение твердого тела. Теорема о движении центра масс. Работа и энергия
Кинематика вращательного движения. Поступательное движение твердого тела. Теорема о движении центра масс. Работа и энергия Презентация по физике "Электроёмкость. Конденсаторы" - скачать
Презентация по физике "Электроёмкость. Конденсаторы" - скачать  Введение в теплотехнику
Введение в теплотехнику Увлекательный мир физики
Увлекательный мир физики Поняття “Ядерна енергетика”
Поняття “Ядерна енергетика”  Презентация по физике "Физика в музыке" - скачать бесплатно
Презентация по физике "Физика в музыке" - скачать бесплатно Бессиловое приближение
Бессиловое приближение Атомно-абсорбционная спектрометрия
Атомно-абсорбционная спектрометрия Почему шуршит пакетик
Почему шуршит пакетик