Содержание
- 2. Теорема о параллельности трех прямых в пространстве Если две прямые параллельны третьей прямой, то они параллельны
- 3. Теорема о параллельности трех прямых в пространстве Если две прямые параллельны третьей прямой, то они параллельны
- 4. Теорема. Две прямые, параллельные третьей прямой, параллельны. . Лемма. Если одна из параллельных прямых пересекает плоскость,
- 5. Две прямые, лежащие в одной плоскости, и не имеющие общих точек, называются параллельными Доказательство от противного.
- 6. Дано: а || c; b || c. Доказать: a || b. Доказательство Предположим, что а
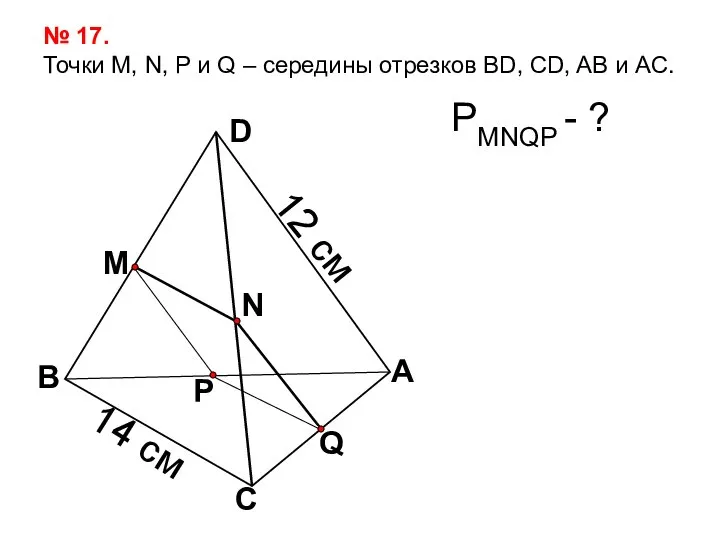
- 7. Задача №17. Дано: М – середина BD A B D C N M Р Q N
- 8. Q А С В D N M P № 17. Точки М, N, P и Q
- 10. Скачать презентацию






 Работу выполнили ученики 7 «А» класса: Никитин Андрей ,
Работу выполнили ученики 7 «А» класса: Никитин Андрей ,  Урок математики в 4 классе. Учитель Павлова Е.Ю. МОУ «Семринская НОШ»
Урок математики в 4 классе. Учитель Павлова Е.Ю. МОУ «Семринская НОШ»  ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ Лекция 7а Развертки поверхностей
Лекция 7а Развертки поверхностей Треугольники вокруг нас - презентация по Геометрии_
Треугольники вокруг нас - презентация по Геометрии_ Луч. Числовой луч.
Луч. Числовой луч. Презентация на тему "Небесная геометрия"
Презентация на тему "Небесная геометрия" Урок по геометрии «Признаки равенства треугольников». 7 класс. АВТОР КРЕСТЬЯНИНОВА ТАТЬЯНА МИХАЙЛОВНА , УЧИТЕЛЬ МАТЕМАТИКИ «М
Урок по геометрии «Признаки равенства треугольников». 7 класс. АВТОР КРЕСТЬЯНИНОВА ТАТЬЯНА МИХАЙЛОВНА , УЧИТЕЛЬ МАТЕМАТИКИ «М ПОСТРОЕНИЕ И ПРЕОБРАЗОВАНИЕ ГРАФИКОВ КВАДРАТИЧНОЙ ФУНКЦИИ - презентация по Геометрии_
ПОСТРОЕНИЕ И ПРЕОБРАЗОВАНИЕ ГРАФИКОВ КВАДРАТИЧНОЙ ФУНКЦИИ - презентация по Геометрии_ Длина окружности и площадь круга. Решение задач.
Длина окружности и площадь круга. Решение задач.  Преобразование симметрии в пространстве. Симметрия в природе и на практике Урок геометрии в 10 классе (базовый уровень) Учитель ма
Преобразование симметрии в пространстве. Симметрия в природе и на практике Урок геометрии в 10 классе (базовый уровень) Учитель ма Признаки равенства прямоугольных треугольников 7 класс Учитель высшей квалификационной категории Стрелюхина Л. М.
Признаки равенства прямоугольных треугольников 7 класс Учитель высшей квалификационной категории Стрелюхина Л. М. Египетский треугольник - презентация по Геометрии
Египетский треугольник - презентация по Геометрии Презентация выполнена учителем математики МОУ лицея № 28 имени Н.А.Рябова г.Тамбова Беляевой О.П.
Презентация выполнена учителем математики МОУ лицея № 28 имени Н.А.Рябова г.Тамбова Беляевой О.П. Многоугольники Демонстрационный материал 8 класс
Многоугольники Демонстрационный материал 8 класс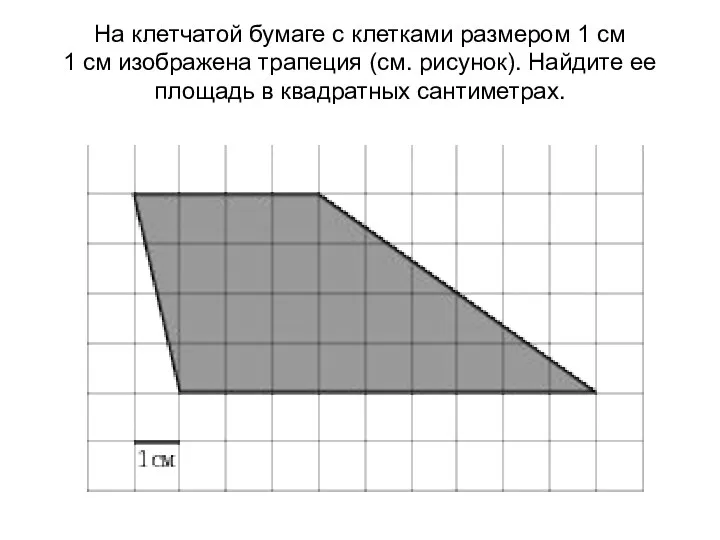 На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах. Окружность и круг методическая разработка Выполнила учитель математики МОУ «Лицей-интернат им. Г.С.Лебедева г.Чебоксары» Селянк
Окружность и круг методическая разработка Выполнила учитель математики МОУ «Лицей-интернат им. Г.С.Лебедева г.Чебоксары» Селянк Чертежи разъемных и неразъемных соединений деталей Выполнила ученица 9 в кл. МОУ лицея №1 Осипянц Милена Учитель черчения Плот
Чертежи разъемных и неразъемных соединений деталей Выполнила ученица 9 в кл. МОУ лицея №1 Осипянц Милена Учитель черчения Плот СЕЧЕНИЯ ПРОСТРАНСТВЕННЫХ ФИГУР Учитель: Попова Т.А. ГБОУ СОШ №684
СЕЧЕНИЯ ПРОСТРАНСТВЕННЫХ ФИГУР Учитель: Попова Т.А. ГБОУ СОШ №684 Объем тел
Объем тел Начальные геометрические сведения Учитель математики МКОУ « Москаленский лицей» Бадюк Ольга Ярославна
Начальные геометрические сведения Учитель математики МКОУ « Москаленский лицей» Бадюк Ольга Ярославна  Виды правильных многогранников - презентация по Геометрии
Виды правильных многогранников - презентация по Геометрии Сложение и вычитание векторов - презентация по Геометрии
Сложение и вычитание векторов - презентация по Геометрии Стояние на реке Угре - презентация по Геометрии
Стояние на реке Угре - презентация по Геометрии Функция у=sin х, ее свойства и график - презентация по Геометрии
Функция у=sin х, ее свойства и график - презентация по Геометрии Применение тригонометрии в жизни
Применение тригонометрии в жизни  Модели многогранников - презентация по Геометрии
Модели многогранников - презентация по Геометрии Теорема Пифагора Пребудет вечной истина, как скоро Её познает слабый человек! И ныне теорема Пифагора Верна, как и в его далёк
Теорема Пифагора Пребудет вечной истина, как скоро Её познает слабый человек! И ныне теорема Пифагора Верна, как и в его далёк