§ 4. Формула включений-исключений. Беспорядки. § 4. Формула включений-исключений. Беспорядки. Теорема 1 (формула включений-исключений). Пусть А = А1 А2…Аm – конечное множество. Тогда
Содержание
- 2. Доказательство. Возьмем элемент а А. В число, стоящее слева, этот элемент «вносит» единицу. Подсчитаем, какое число
- 3. единиц, так как a входит во все пересечения такие, что и содержат a; число таких пересечений
- 4. Чтобы доказать теорему, осталось доказать равенство Но это равенство равносильно следующему :
- 5. которое верно, так как является следствием бинома Ньютона при х = -1. Теорема доказана.
- 6. Наиболее часто формулу включений-исключений применяют в несколько иной формулировке. Пусть имеется N предметов, каждый из которых
- 7. Теорема 2.
- 8. Пример. Вычислить количество натуральных чисел, не превосходящих 100, которые не делятся на 2, 3, 5. Решение.
- 9. Определение 3. Пусть дано множество А = {1, 2, 3, …, n}. Перестановка (к1, к2,…, кn)
- 10. Теорема 4. Число беспорядков n-элементного множества равно Доказательство. Введем обозначения: N(i) – количество перестановок, у которых
- 11. Пусть N(i1, i2, …, ik ) – количество перестановок, в которых числа i1, i2, …, ik
- 14. Скачать презентацию





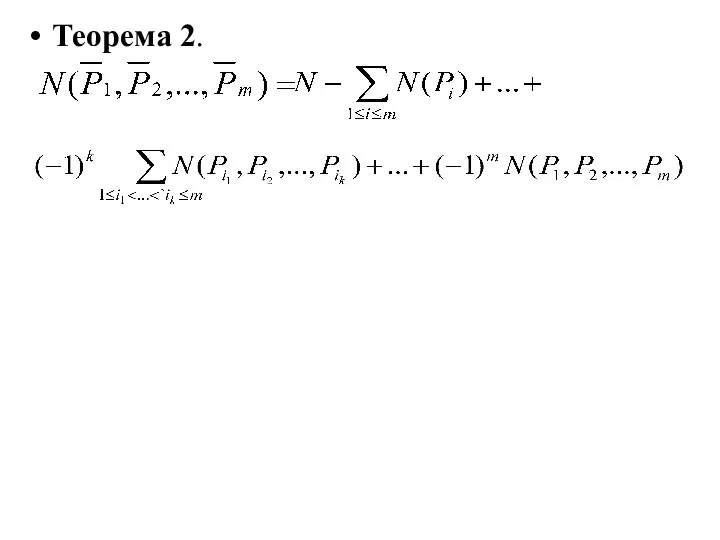




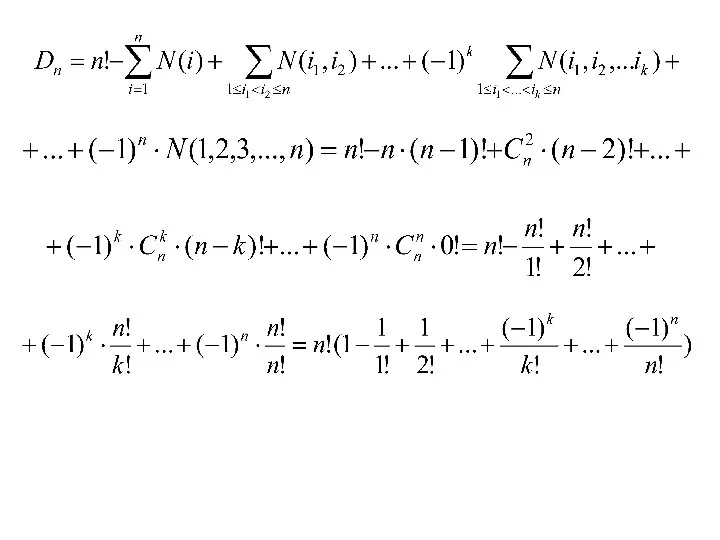
 Подобные треугольники
Подобные треугольники Текстовые задачи. ЕГЭ-2014. В-14
Текстовые задачи. ЕГЭ-2014. В-14 Проценты вокруг нас
Проценты вокруг нас Функция y=sinx
Функция y=sinx Делимость произведения
Делимость произведения Задачи со спичками. Площади фигур. 7 класс
Задачи со спичками. Площади фигур. 7 класс Визначники матриць (продовження). Системи лінійних рівнянь
Визначники матриць (продовження). Системи лінійних рівнянь Футбол. Дидактическая игра по математике, 2 класс
Футбол. Дидактическая игра по математике, 2 класс Лекция 6. Корреляционный и регрессионный анализ
Лекция 6. Корреляционный и регрессионный анализ Свойства степени с рациональным показателем
Свойства степени с рациональным показателем Сложение, вычитание и умножение обыкновенных дробей
Сложение, вычитание и умножение обыкновенных дробей Квадратные уравнения
Квадратные уравнения Умножение десятичных дробей на натуральное число.
Умножение десятичных дробей на натуральное число. Повторяем таблицу умножения вместе с Машей
Повторяем таблицу умножения вместе с Машей Признаки равенства треугольников
Признаки равенства треугольников Основное свойство дроби
Основное свойство дроби Замена переменной и формула интегрирования по частям в определенном интеграле
Замена переменной и формула интегрирования по частям в определенном интеграле Презентация по математике "Умножение и деление на 10" - скачать
Презентация по математике "Умножение и деление на 10" - скачать  Графические задания ЕГЭ. Чтение свойств функции по графику и распознавание графиков элементарных функций
Графические задания ЕГЭ. Чтение свойств функции по графику и распознавание графиков элементарных функций Области определения графика
Области определения графика Столько же и еще… Столько же, но без… Урок математики в 1 «Б» классе УМК «Перспектива» Мостовщикова О.А. МОУ «СОШ №5 город Саратов
Столько же и еще… Столько же, но без… Урок математики в 1 «Б» классе УМК «Перспектива» Мостовщикова О.А. МОУ «СОШ №5 город Саратов  Числовая окружность
Числовая окружность Логика
Логика Среднее арифметическое
Среднее арифметическое Иностранные меры длины
Иностранные меры длины Многогранники в нашей жизни
Многогранники в нашей жизни Применение производных Лекция 6
Применение производных Лекция 6  Задачи на увеличение числа на несколько единиц (с двумя множествами предметов)
Задачи на увеличение числа на несколько единиц (с двумя множествами предметов)