Содержание
- 2. Теорема: Для того чтобы дифференцировать выражение , где и определены и непрерывны в области плоскости и
- 3. Интегрирующий множитель.
- 4. Если , то уравнение не является уравнением в полных дифференциалах. Однако это уравнение можно превратить в
- 5. Практически поступают так: берут выражение , делят на , если не зависит частное от , то
- 6. 6.Дополнительные сведения.
- 7. Дифференциальное уравнение может быть также истолковано следующим образом. Пусть - общее решение дифференциального уравнения, т.е. семейство
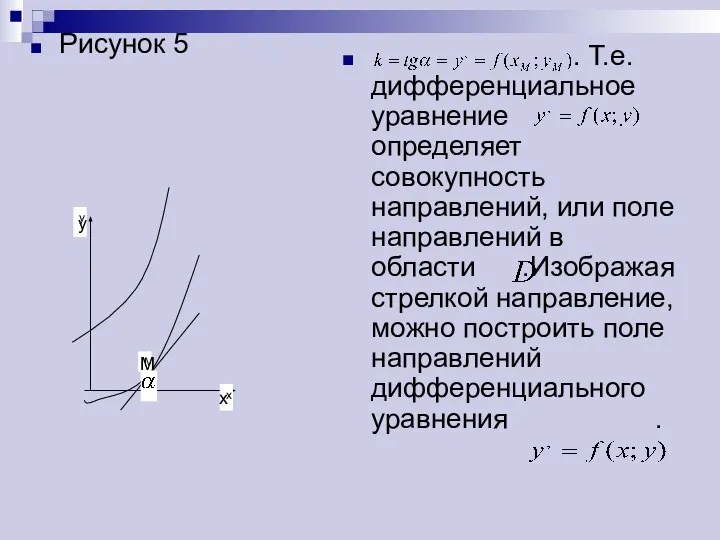
- 8. Рисунок 5 . Т.е. дифференциальное уравнение определяет совокупность направлений, или поле направлений в области .Изображая стрелкой
- 9. Геометрически задача интегрирования дифференциального уравнения заключается в нахождении кривых, которые в каждой своей точке касаются направления,
- 10. Теорема (Коши). Если функция определена и непрерывна в области плоскости и имеет непрерывную частную производную во
- 11. 7. Уравнение первого порядка, не разрешенные относительно производной.
- 12. Рассмотрим дифференциальное уравнение , не разрешенное относительно .
- 13. Случай 1. Уравнение первого порядка n-й степени , где n-целое положительное число, , - функции от
- 14. Получили :
- 15. Общие интегралы имеют вид:
- 16. Случай 2. Уравнение разрешенное относительно у и не содержащее х . Это уравнение решается методом введения
- 17. Пусть , тогда .
- 18. Случай 3. Уравнение разрешенное относительно х и не содержащее у: . Аналогично: ,
- 19. Случай 4. . Уравнения не содержащие х и у, но не обязательно разрешенные относительно у и
- 20. Случай 5. Уравнение Лагранжа. Уравнение, линейно относительно x и y , т.е. имеющее вид
- 21. 1-й случай . Его общий интеграл имеет вид , вместе с уравнением он дает общий интеграл
- 22. 2-й случай .
- 24. Скачать презентацию



















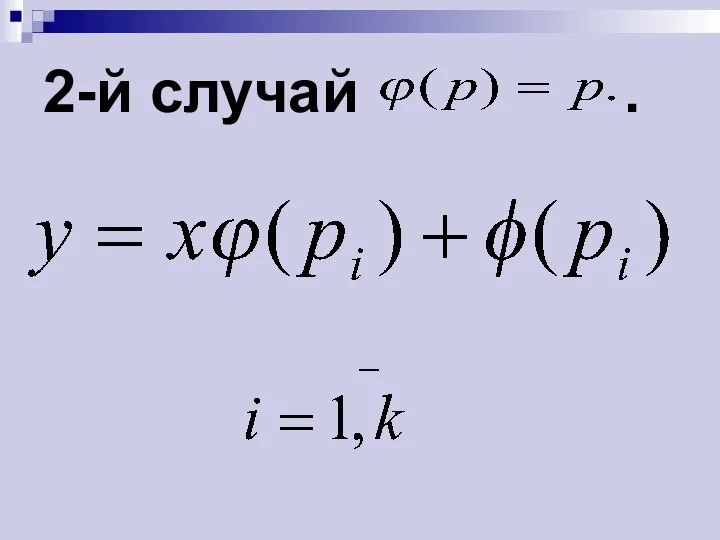
 Линейная функция, её график и свойства
Линейная функция, её график и свойства Иррациональные числа. История открытия
Иррациональные числа. История открытия 10 способов решения квадратных уравнений
10 способов решения квадратных уравнений Множественная регрессия
Множественная регрессия Построение графиков тригонометрических функций
Построение графиков тригонометрических функций Эталоны единиц измерений
Эталоны единиц измерений Аттестационная работа. Образовательная программа мастерской «Интеграл» общеинтеллектуального направления
Аттестационная работа. Образовательная программа мастерской «Интеграл» общеинтеллектуального направления Правильные и неправильные дроби. Смешанные числа. 5 класс
Правильные и неправильные дроби. Смешанные числа. 5 класс Задачи по геометрии 11 класс
Задачи по геометрии 11 класс Достоверность опубликованных данных об исследованиях.
Достоверность опубликованных данных об исследованиях. Осевая и центральная симметрии
Осевая и центральная симметрии Подготовка к контрольной работе по математике, 5 класс
Подготовка к контрольной работе по математике, 5 класс Система линейных уравнений
Система линейных уравнений Решение текстовых задач
Решение текстовых задач Действия со степенями и корнями
Действия со степенями и корнями Комплексные числа. Формы записи
Комплексные числа. Формы записи Животные в мире математики
Животные в мире математики Дискретная математика
Дискретная математика Определение логарифма
Определение логарифма Класс точности СИ и его обозначение. Погрешности измерений. Источники и классификация погрешностей измерений
Класс точности СИ и его обозначение. Погрешности измерений. Источники и классификация погрешностей измерений Математические игры по-олимпийски
Математические игры по-олимпийски Цилиндр, конус, шар
Цилиндр, конус, шар Понятие смешанной дроби
Понятие смешанной дроби Теорема Пифагора
Теорема Пифагора Магический квадрат. Соревнование среди учащихся 7a классa
Магический квадрат. Соревнование среди учащихся 7a классa Математика вокруг нас
Математика вокруг нас Способы решения квадратных уравнений
Способы решения квадратных уравнений Математический диктант № 9. 2 класс
Математический диктант № 9. 2 класс