Содержание
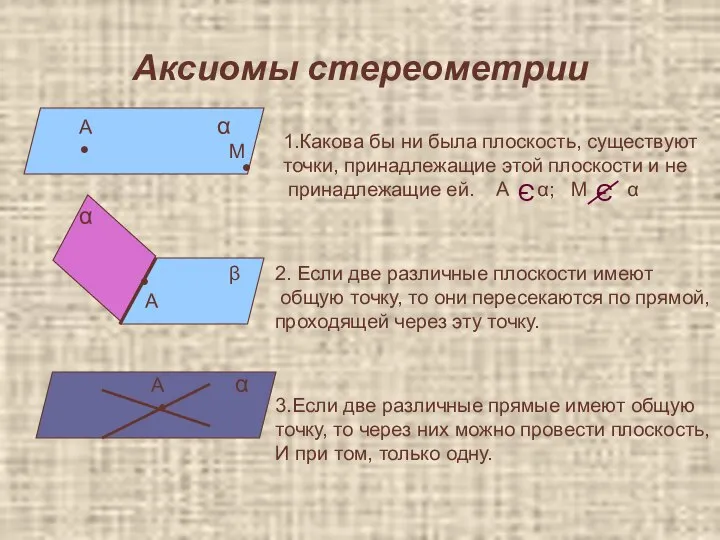
- 2. Аксиомы стереометрии • • • • А М А А α α α β 1.Какова бы
- 3. Параллельность прямой и плоскости α а Прямую и плоскость называют параллель- ными, если они не пересекаются.
- 4. Параллельность прямой и плоскости Признак Если прямая, не принадлежащая плоскости, параллельна прямой, принадлежащей этой плоскости, то
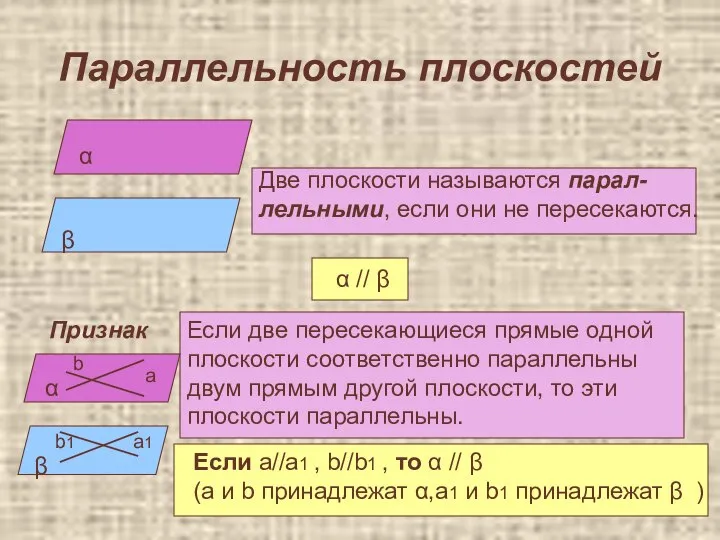
- 5. Параллельность плоскостей Две плоскости называются парал- лельными, если они не пересекаются. α // β Признак Если
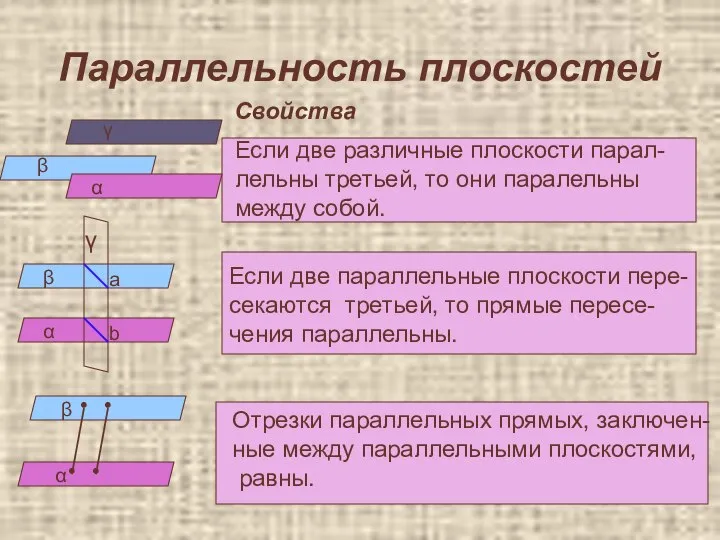
- 6. Параллельность плоскостей Свойства α β γ Если две различные плоскости парал- лельны третьей, то они паралельны
- 7. Перпендикулярность прямой и плоскости Прямую, пересекающую плоскость, называют перпендикулярной к этой плоскости, если она перпендикулярна любой
- 8. Перпендикулярность прямой и плоскости Признак перпендикулярности прямой и плоскости Если прямая перпендикулярна двум пересекающимся прямым, лежащим
- 9. Перпендикулярность прямой и плоскости Свойства перпендикулярных прямой и плоскости • • α а b Если плоскость
- 10. Теорема о трех перпендикулярах α А О В с Если прямая на плоскости перпенди- кулярна проекции
- 11. Перпендикулярность плоскостей α β γ Две пересекающиеся плоскости называют перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения
- 12. Перпендикулярность плоскостей Признак Свойство Если плоскость проходит через прямую, перпенди- кулярную другой плоскос- ти, то эти
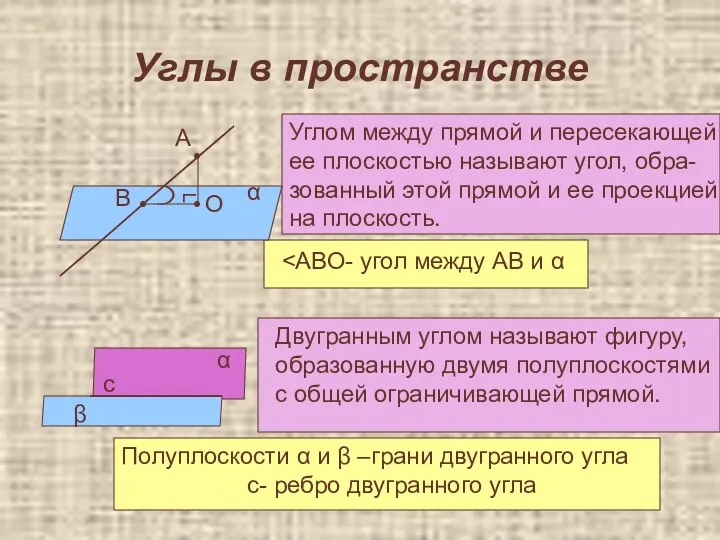
- 13. Углы в пространстве α • • ┐ А В О • Углом между прямой и пересекающей
- 14. Линейный угол двугранного угла α β с А М В Линейным углом двугранного угла называют угол
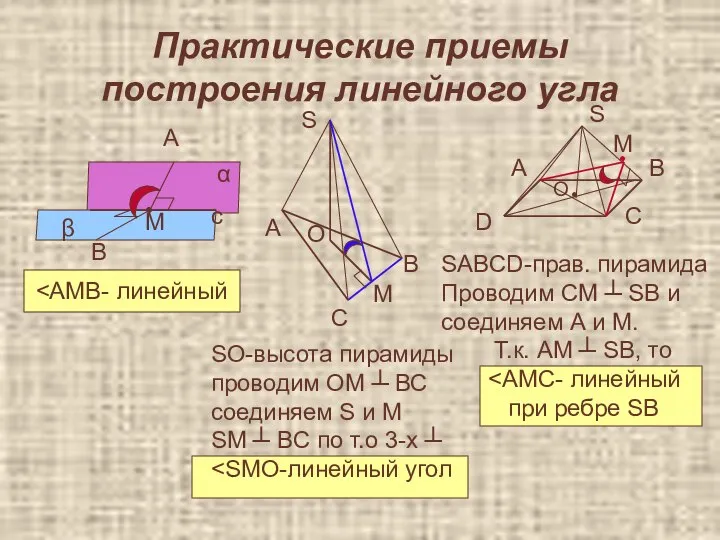
- 15. Практические приемы построения линейного угла β α с • А М В А С М В
- 16. Угол между скрещивающимися прямыми а b a1 b1 φ Углом между скрещивающи- мися прямыми называют угол
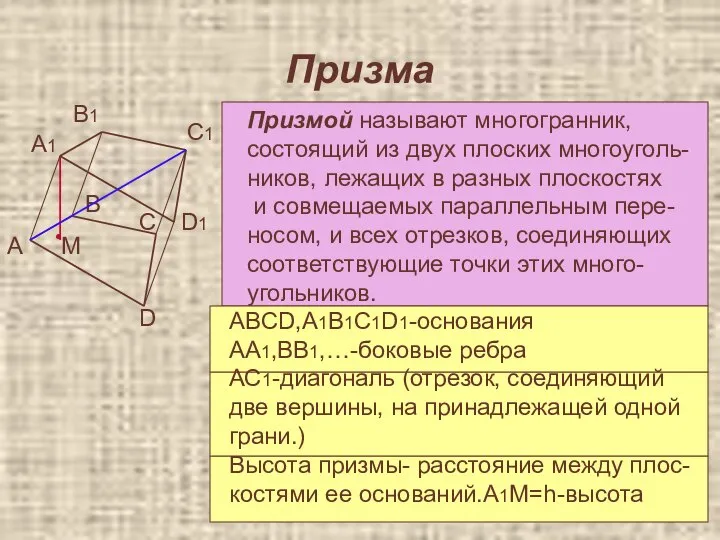
- 17. Призма Призмой называют многогранник, состоящий из двух плоских многоуголь- ников, лежащих в разных плоскостях и совмещаемых
- 18. Свойства призмы Основания призмы равны. Основания призмы лежат в парал- лельных плоскостях. Боковые ребра призмы параллельны
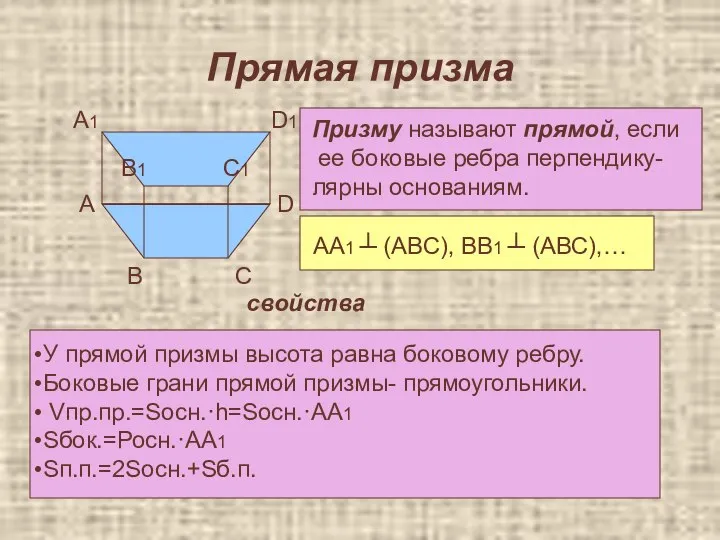
- 19. Прямая призма А А1 В В1 С С1 D D1 Призму называют прямой, если ее боковые
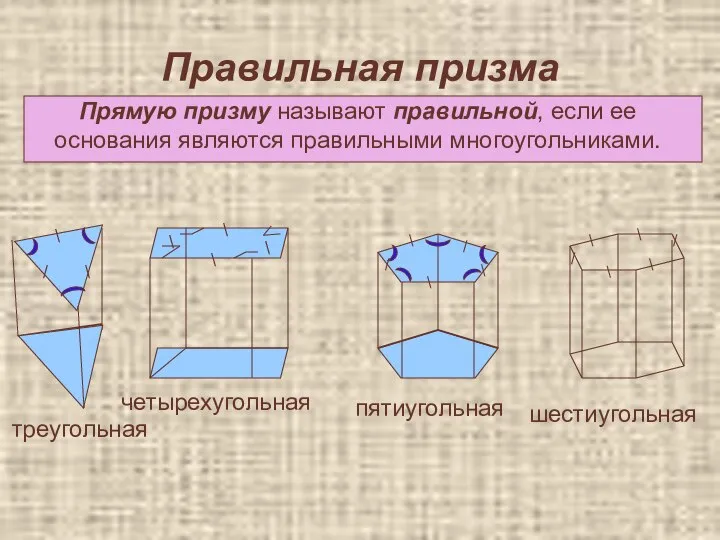
- 20. Правильная призма Прямую призму называют правильной, если ее основания являются правильными многоугольниками. треугольная \ \ /
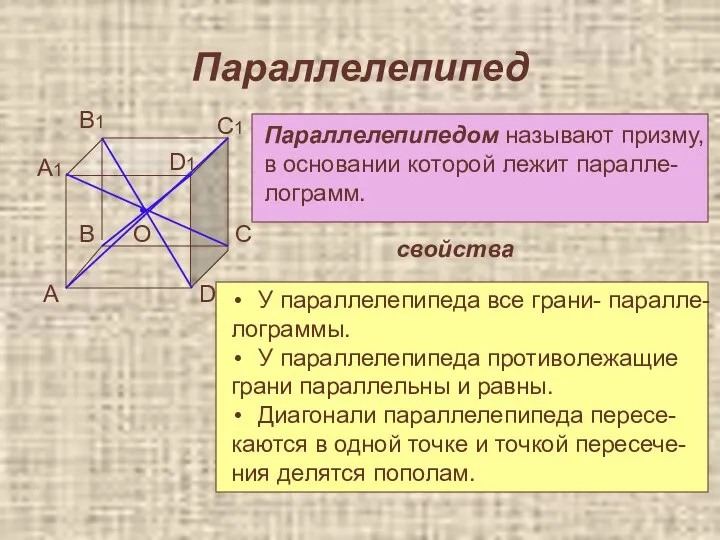
- 21. Параллелепипед А В С D A1 B1 C1 D1 Параллелепипедом называют призму, в основании которой лежит
- 22. Параллелепипед Прямоугольный параллелепипед-это параллелепипед, у которого основанием является прямоугольник. а b c d Свойства У прямоугольного
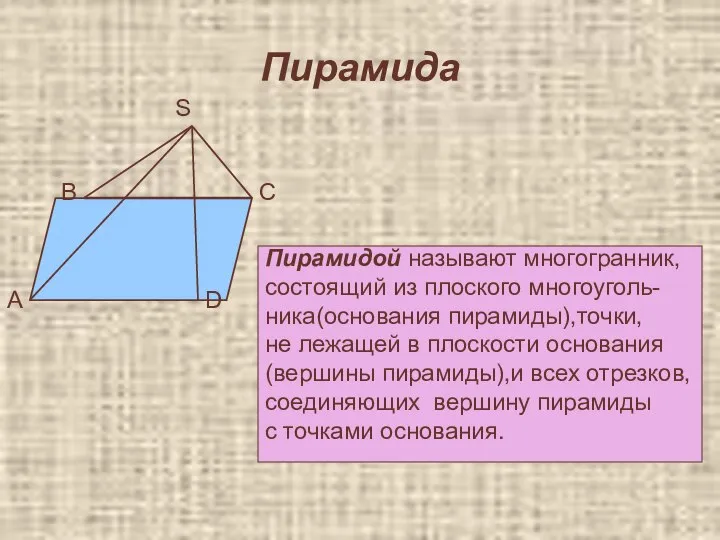
- 23. Пирамида Пирамидой называют многогранник, состоящий из плоского многоуголь- ника(основания пирамиды),точки, не лежащей в плоскости основания (вершины
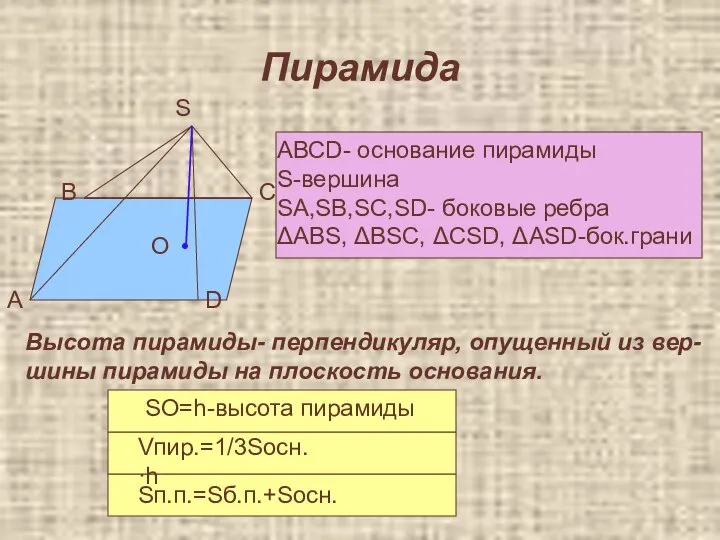
- 24. Пирамида АВСD- основание пирамиды S-вершина SA,SB,SC,SD- боковые ребра ΔABS, ΔBSC, ΔCSD, ΔASD-бок.грани Высота пирамиды- перпендикуляр, опущенный
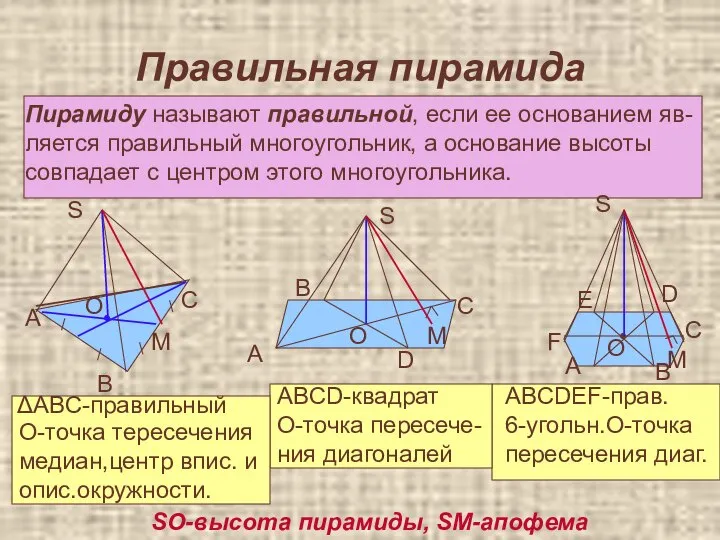
- 25. Правильная пирамида Пирамиду называют правильной, если ее основанием яв- ляется правильный многоугольник, а основание высоты совпадает
- 26. Правильная пирамида Свойства У правильной пирамиды боковые ребра равны и одинаково наклонены к плоскости основания. Боковые
- 27. Положение высоты в некоторых видах пирамид 1.Если все боковые ребра пирамиды равны или наклонены под одним
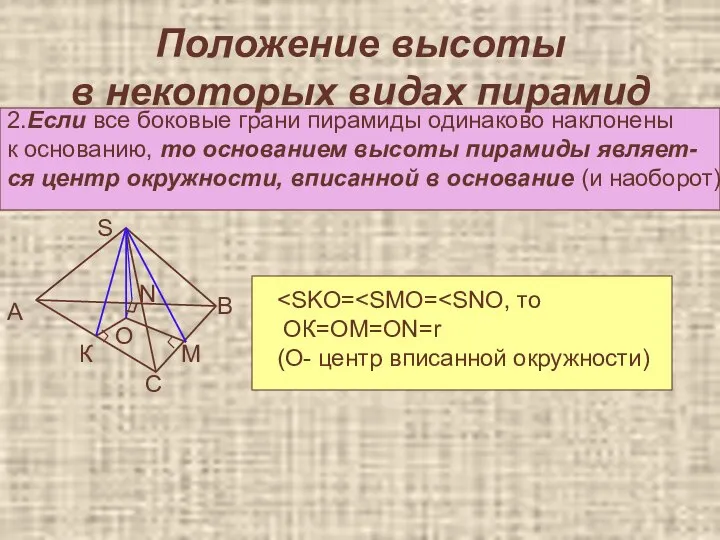
- 28. Положение высоты в некоторых видах пирамид 2.Если все боковые грани пирамиды одинаково наклонены к основанию, то
- 29. Положение высоты в некоторых видах пирамид 3.Если все боковые грани пирамиды одинаково наклонены к плоскости основания,
- 30. Положение высоты в некоторых видах пирамид 4.Если только две боковые грани пирамиды одинаково накло- нены к
- 31. Положение высоты в некоторых видах пирамид 5.Если только одна боковая грань пирамиды перпенди- кулярна плоскости основания,
- 32. Положение высоты в некоторых видах пирамид 6.Если две смежные боковые грани пирамиды перпендику- лярны плоскости основания,
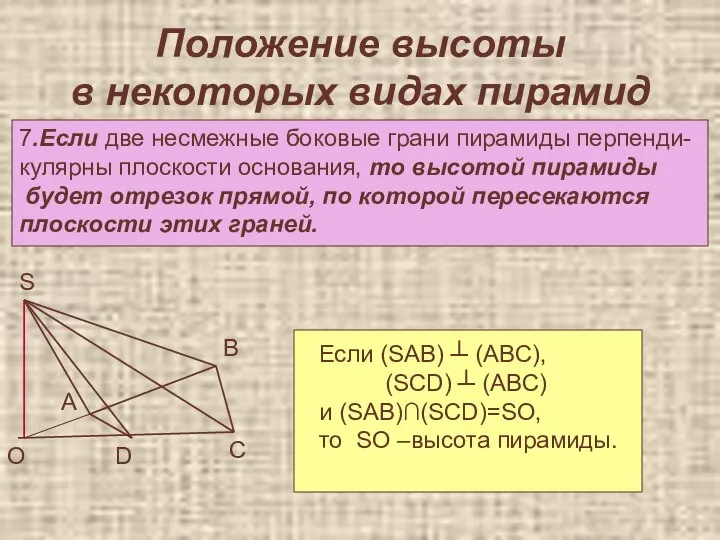
- 33. Положение высоты в некоторых видах пирамид 7.Если две несмежные боковые грани пирамиды перпенди- кулярны плоскости основания,
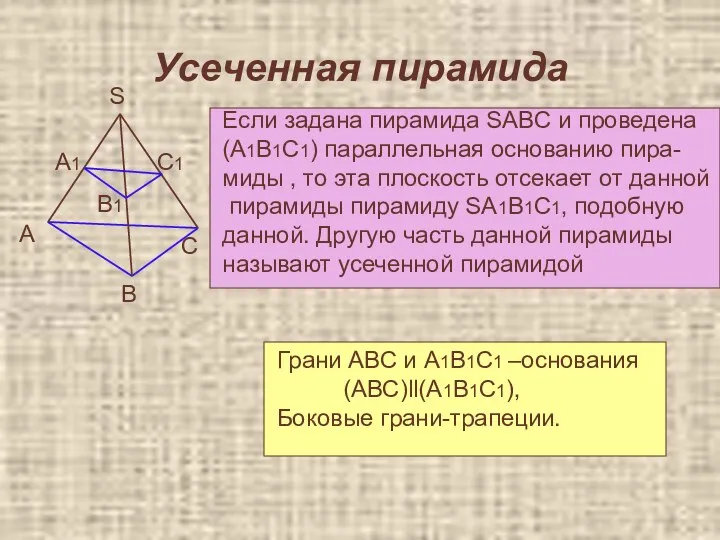
- 34. Усеченная пирамида Если задана пирамида SABC и проведена (A1B1C1) параллельная основанию пира- миды , то эта
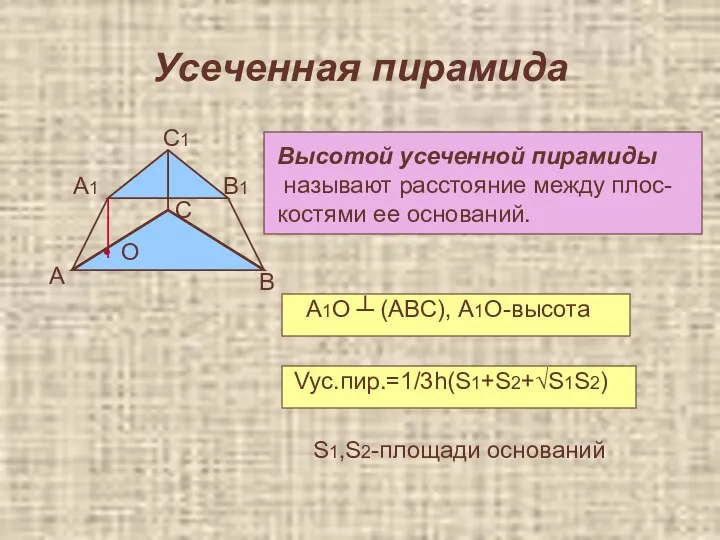
- 35. Усеченная пирамида • А В С А1 С1 В1 О Высотой усеченной пирамиды называют расстояние между
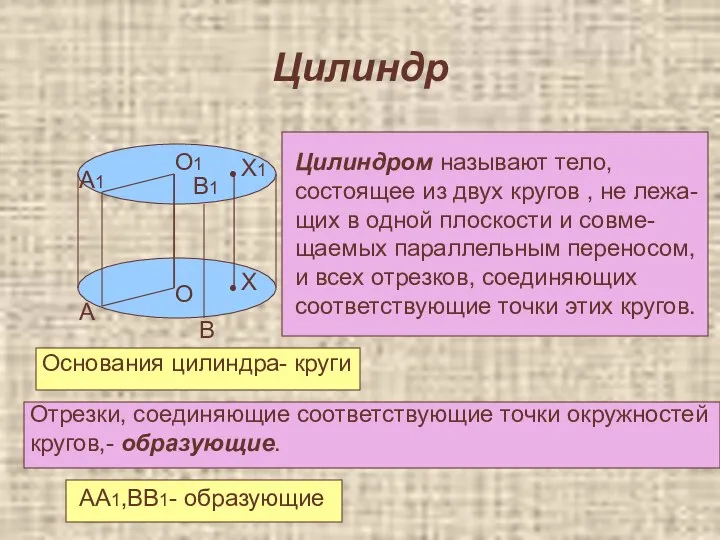
- 36. Цилиндр О О1 А А1 Х Х1 • • Цилиндром называют тело, состоящее из двух кругов
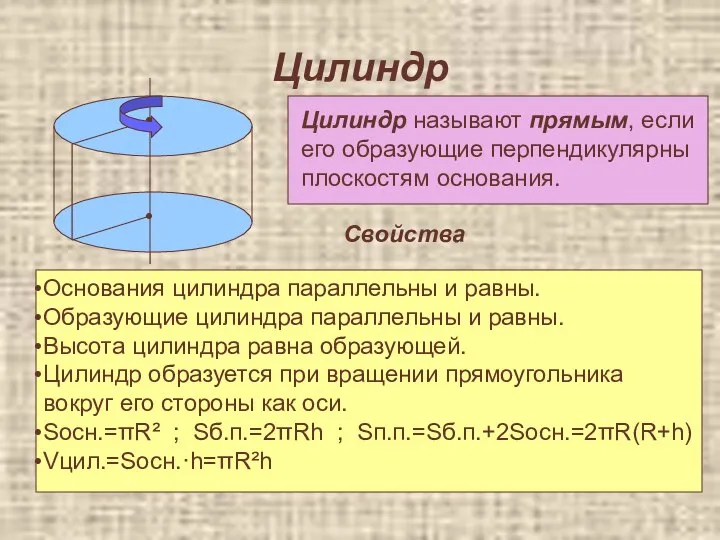
- 37. Цилиндр Цилиндр называют прямым, если его образующие перпендикулярны плоскостям основания. Свойства Основания цилиндра параллельны и равны.
- 38. Сечение цилиндра плоскостями • • АВСD-осевое сечение-прямоугольник AD=2R, AB=h А В С D O O1 •
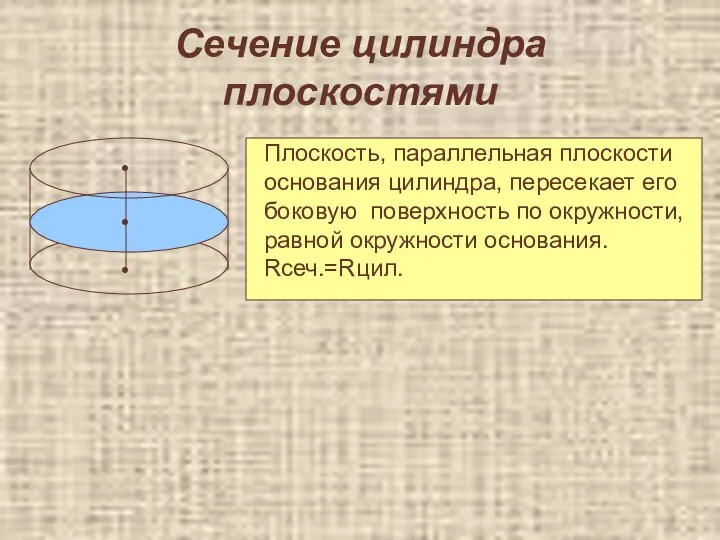
- 39. Сечение цилиндра плоскостями • • • Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по
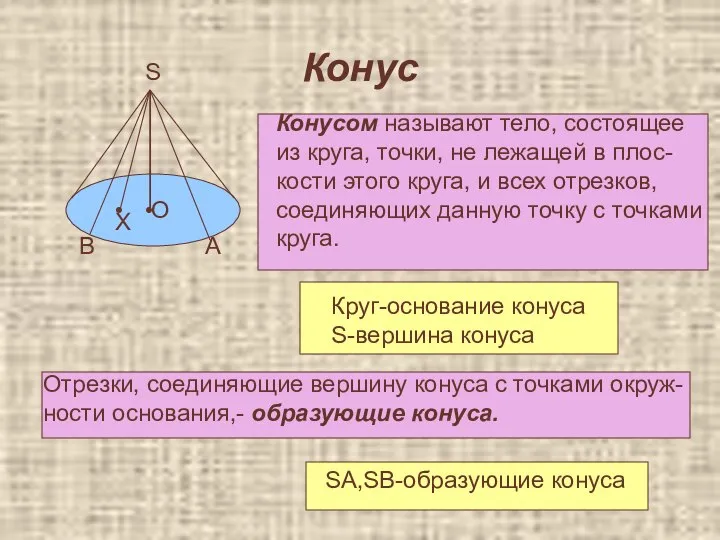
- 40. Конус • • S O X A B Конусом называют тело, состоящее из круга, точки, не
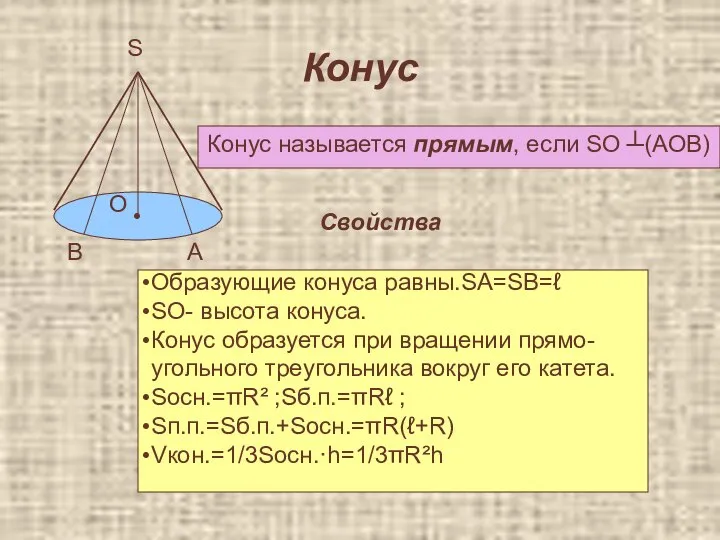
- 41. Конус • Конус называется прямым, если SO ┴(AOB) S O A B Свойства Образующие конуса равны.SА=SB=ℓ
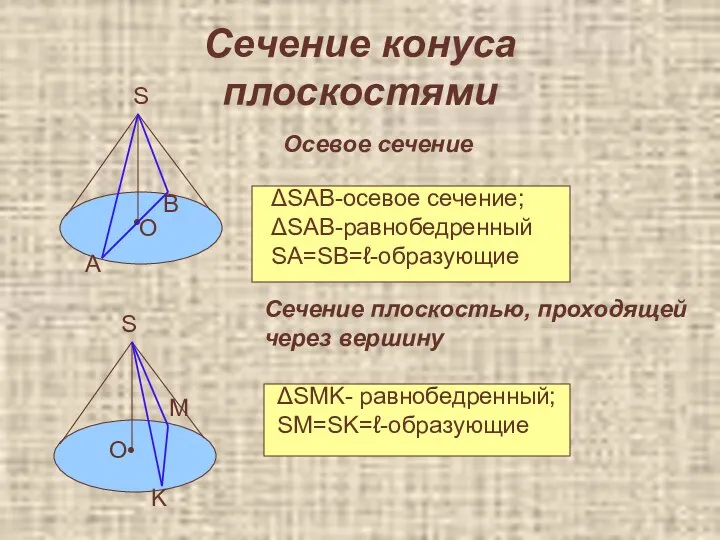
- 42. Сечение конуса плоскостями Осевое сечение А О В S ΔSAB-осевое сечение; ΔSAB-равнобедренный SA=SB=ℓ-образующие Сечение плоскостью, проходящей
- 43. Сечение конуса плоскостями • О О1 S Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу,
- 44. Усеченный конус • • О О1 В А S Если в данном конусе проведена плоскость, параллельная
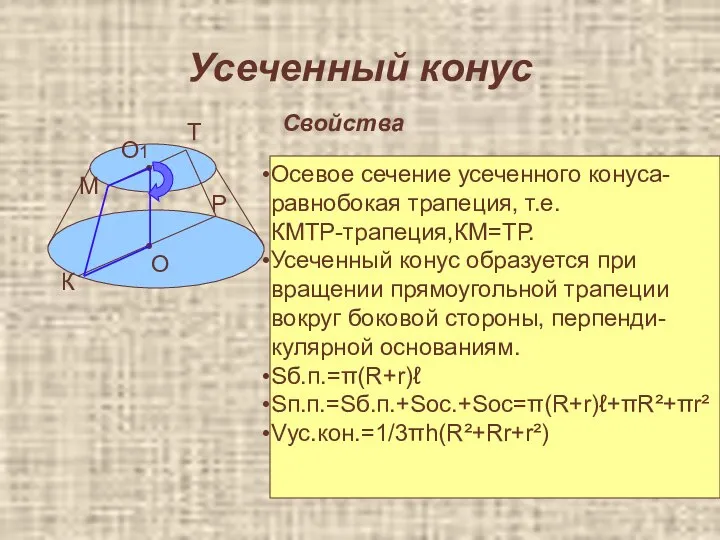
- 45. Усеченный конус Свойства • • О О1 К М Т Р Осевое сечение усеченного конуса- равнобокая
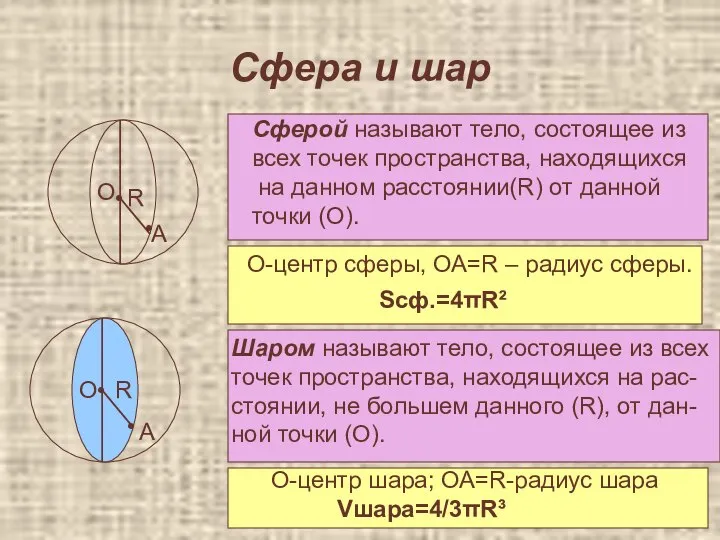
- 46. Сфера и шар • А R Сферой называют тело, состоящее из всех точек пространства, находящихся на
- 48. Скачать презентацию





















 Перестановки. Лекция 23
Перестановки. Лекция 23 Степень с целым показателем
Степень с целым показателем Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс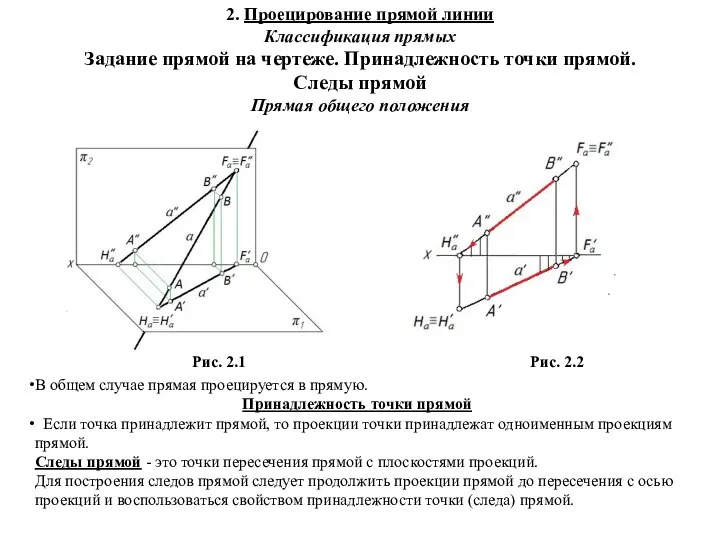 Предмет начертательной геометрии. Проецирование прямой линии. Классификация прямых. Задание прямой на чертеже. (Лекция 2)
Предмет начертательной геометрии. Проецирование прямой линии. Классификация прямых. Задание прямой на чертеже. (Лекция 2) Призмы и антипризмы
Призмы и антипризмы Пересечение поверхностей
Пересечение поверхностей Понятие логарифма
Понятие логарифма Проверка деления с остатком
Проверка деления с остатком Совместные действия с обыкновенными и десятичными дробями
Совместные действия с обыкновенными и десятичными дробями Координатная плоскость. Алгебра 7 класс
Координатная плоскость. Алгебра 7 класс Эталоны и их классификация. (Лекция 3)
Эталоны и их классификация. (Лекция 3) Четвертое измерение
Четвертое измерение Тест по теме: "Векторы в пространстве. Сложение и вычитание векторов. Умножение вектора на число". Вариант 2
Тест по теме: "Векторы в пространстве. Сложение и вычитание векторов. Умножение вектора на число". Вариант 2 Площадь треугольника
Площадь треугольника Метод координат
Метод координат Прямоугольные треугольники
Прямоугольные треугольники Задача двух тел. Уравнения движения в задаче двух тел
Задача двух тел. Уравнения движения в задаче двух тел Виды треугольников. 5 класс
Виды треугольников. 5 класс Пространственные фигуры. Площадь, объем
Пространственные фигуры. Площадь, объем ЛИНЕЙНАЯ ФУНКЦИЯ» Презентация по алгебре для 7 класса
ЛИНЕЙНАЯ ФУНКЦИЯ» Презентация по алгебре для 7 класса  Познайте мир логических задач. Математика и логика неразделимы
Познайте мир логических задач. Математика и логика неразделимы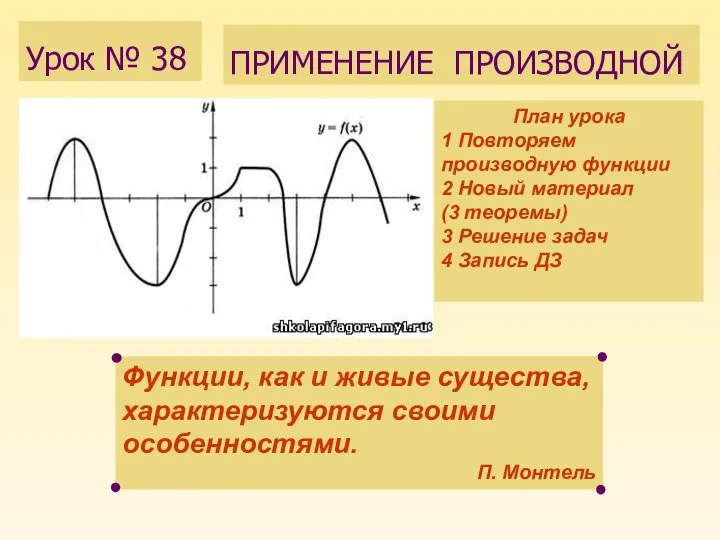 Правила дифференцирования
Правила дифференцирования Числовой отрезок
Числовой отрезок Бирелгән почмакка тигез почмакны циркуль һәм линейка ярдәмендә ничек төзергә
Бирелгән почмакка тигез почмакны циркуль һәм линейка ярдәмендә ничек төзергә Деление десятичных дробей на натуральное число
Деление десятичных дробей на натуральное число Задачи на дроби (3). 6 класс
Задачи на дроби (3). 6 класс Определение и признаки параллелограмма
Определение и признаки параллелограмма Таблица основных неопределенных интегралов
Таблица основных неопределенных интегралов