Содержание
- 2. Правила дифференцирования
- 3. Формулы дифференцирования
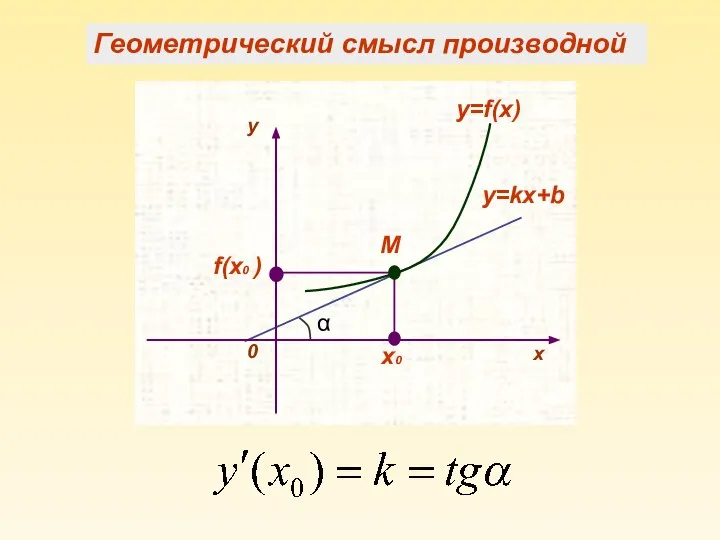
- 4. Геометрический смысл производной
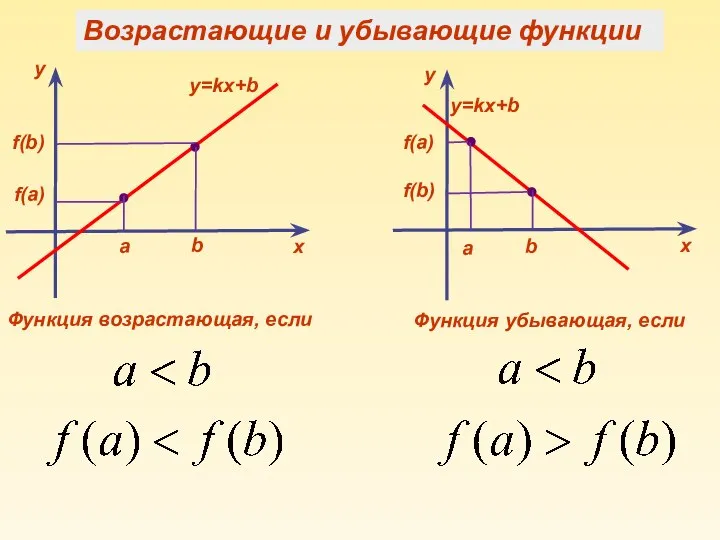
- 5. Функция возрастающая, если Функция убывающая, если Возрастающие и убывающие функции
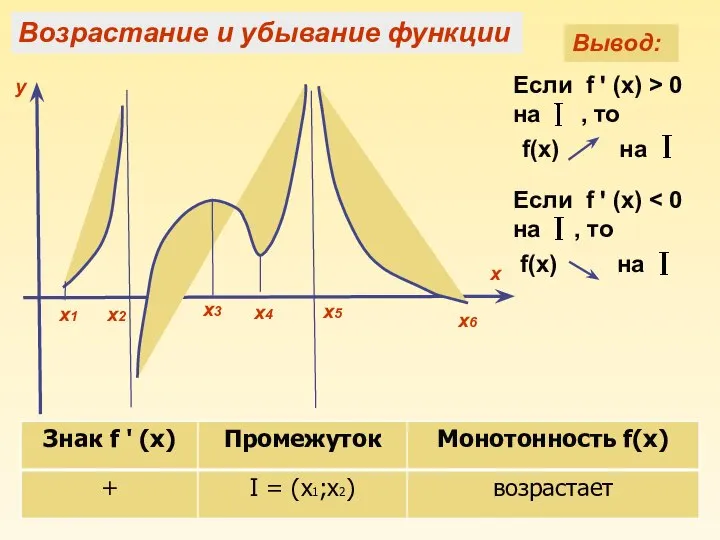
- 6. Вывод: Если f ꞌ (x) > 0 на , то Если f ꞌ (x) f(x) на
- 7. Теорема Лагранжа Теорема 1: Если функция y=f(x) непрерывна на [a;b] и дифференцируема на (a;b), то существует
- 8. Теорема 2: Если функция y=f(x) дифференцируема на (a;b), и f ꞌ(x)>0 для всех х Є (a;b),
- 9. № 900(1,3,5,7),902(1,3),903(1,3),904(1),905(1)
- 11. Скачать презентацию


![Теорема Лагранжа Теорема 1: Если функция y=f(x) непрерывна на [a;b] и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/652965/slide-6.jpg)


 Понятие алгоритма. Свойства алгоритмов. Формы записей алгоритмов. Общие принципы построения алгоритмов
Понятие алгоритма. Свойства алгоритмов. Формы записей алгоритмов. Общие принципы построения алгоритмов Цифры и числа Интеллектуальная игра 8 – 9 классы
Цифры и числа Интеллектуальная игра 8 – 9 классы Математические модели неодномерных нестационарных течений газа
Математические модели неодномерных нестационарных течений газа Правильные фигуры и тела
Правильные фигуры и тела Решение неравенств ГБОУ СОШ №1084 Учитель математики Смирнова Н.В.
Решение неравенств ГБОУ СОШ №1084 Учитель математики Смирнова Н.В. Постройте сечение куба и тетраэдра
Постройте сечение куба и тетраэдра Уравнение-следствие. Возведение уравнения в четную степень
Уравнение-следствие. Возведение уравнения в четную степень Сложение и вычитание дробей с разными знаменателями.
Сложение и вычитание дробей с разными знаменателями. Величины и их измерение. (Тема 4)
Величины и их измерение. (Тема 4) Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Масштаб. Виды масштаба
Масштаб. Виды масштаба Диференціальні рівняння. Загальні визначення (лекція 4)
Диференціальні рівняння. Загальні визначення (лекція 4) Министерство образования и науки Республики Бурятия МО «Кабанский район МОУ «Выдринская средняя общеобразовательная школ
Министерство образования и науки Республики Бурятия МО «Кабанский район МОУ «Выдринская средняя общеобразовательная школ Функция y = x и её график
Функция y = x и её график Математика в моей будущей профессии металлурга
Математика в моей будущей профессии металлурга Презентация на тему Пифагор
Презентация на тему Пифагор ЕГЭ по математике. Решение заданий В13 (задачи на прогрессии
ЕГЭ по математике. Решение заданий В13 (задачи на прогрессии Разложение многочлена на множители. урок-путешествие
Разложение многочлена на множители. урок-путешествие Квадратичная функция
Квадратичная функция Презентация по математике "Прямая и обратная пропорциональность" - скачать
Презентация по математике "Прямая и обратная пропорциональность" - скачать  Определение степени с натуральным показателем
Определение степени с натуральным показателем Adunarea numerelor negative
Adunarea numerelor negative Арифметический квадратный корень
Арифметический квадратный корень Десятичная запись дробей
Десятичная запись дробей Аттестационная работа. Применение исследовательской и проектной деятельности в учебно-воспитательном процессе
Аттестационная работа. Применение исследовательской и проектной деятельности в учебно-воспитательном процессе Действительные числа
Действительные числа Координатная плоскость (урок 1)
Координатная плоскость (урок 1) Готовимся к ЕГЭ-2015 по математике. Решение 1 части реального теста ЕГЭ-2014
Готовимся к ЕГЭ-2015 по математике. Решение 1 части реального теста ЕГЭ-2014