Содержание
- 2. Про соревнования 3 мая 2013 Соревнования будут проходить в пятницу 3 мая, с 14-00, в 305-307
- 3. План лекции Перестановки и инверсии Инверсии Связь со сложностью сортировки Алгоритм восстановления перестановки по таблице инверсий
- 4. Перестановки Перестановкой порядка N называется расположение N различных объектов в ряд в некотором порядке Для объектов
- 5. Перестановки Для множества из N элементов можно построить N! различных перестановок Первую позицию можно занять N
- 6. Пусть даны множество из N элементов 1,2, 3,..., N и его перестановка Пара называется инверсией (инверсионной
- 7. Перестановка 4, 1, 3, 2 имеет четыре инверсии (4,1), (3,2), (4,3) и (4,2) Почему? Инверсии --
- 8. Таблица инверсий Таблицей инверсий перестановки а1, а2, ..., aN называется последовательность чисел b1, b2, …, bN,
- 9. Свойства таблиц инверсий Для элементов таблицы инверсий справедливы неравенства bN = 0 0 0 Таблица инверсий
- 10. Построение перестановки по таблице инверсий На каждом шаге вставляем следующий по величине элемент с учетом того,
- 11. Построение перестановки по таблице инверсий справа налево Вход N > 0 - количество элементов перестановки b1,
- 12. Создается заготовка пустой перестановки длины N На каждом шаге для каждого элемента перестановки, начиная с 1,
- 13. Построение перестановки по таблице инверсий слева направо Вход N > 0 - количество элементов перестановки b1,
- 14. Инверсионный метод поиска всех перестановок Таблицы инверсий взаимно однозначно соответствуют перестановкам Почему? Перебор ТИ сводится к
- 15. Инверсионный метод поиска всех перестановок Рассмотрим таблицу инверсий как N-значное число в «системе счисления», где количество
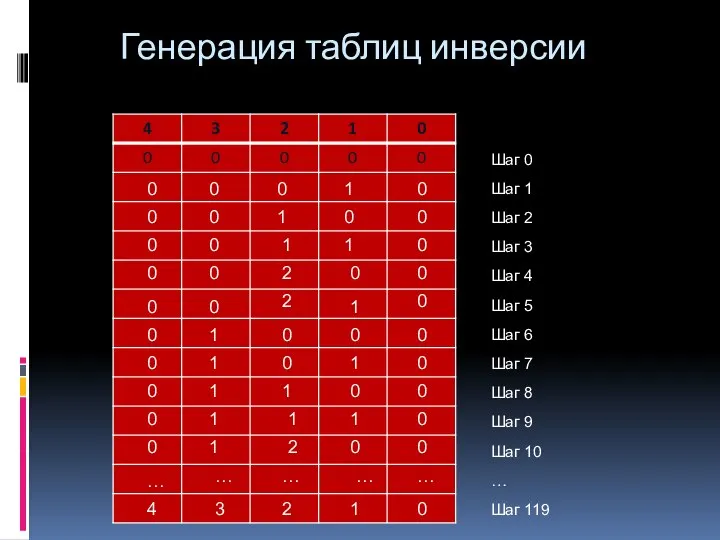
- 16. Генерация таблиц инверсии 0 0 0 0 0 0 0 0 0 1 1 1 …
- 17. Нахождение следующей таблицы инверсий B = b1, b2, ..., bN – ТИ i = N не_всё
- 18. Поиск следующей по алфавиту перестановки (алг. Дейкстры) П. b = b1, b2, …, bN предшествует п.
- 19. Алгоритм Дейкстры От заданной перестановки перейдем к следующей за ней в алфавитном порядке и т.д., пока
- 20. Генерация следующей по алфавиту перестановки Вход П = a1, a2, …, a[N-1], aN – перестановка N
- 21. Для перестановки 1 4 6 2 9 5 8 7 3 Найти следующую по алфавиту. 1
- 22. Рекурсивный метод поиска всех перестановок
- 23. Пример рекурсивного перебора для M= {1,2,3,4} Реr(M) Р ({2,3,4}) Р ({1,3,4}) Р ({1,2,4}) Р ({1,2,3}) Р
- 24. Реализация на языке Си typedef char string[256]; void permut(string start, string rest) { int lenr =
- 25. Реализация на языке Си #include typedef char mystring_t[256]; void permut(mystring_t start, mystring_t rest) { int lenr
- 26. Генерация всех перестановок методом Кнута Идея Рекурсивная генерация начиная с пустой перестановки методом расширения базового множества
- 27. Генерация перестановок методом Кнута – способ 1 Пусть дана перестановка длины N Допишем в конец перестановки
- 28. Генерация перестановок методом Кнута – способ 2 Пусть дана перестановка длины N: a1 a2 … aN
- 30. Скачать презентацию





















![Реализация на языке Си typedef char string[256]; void permut(string start, string](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1442865/slide-23.jpg)
![Реализация на языке Си #include typedef char mystring_t[256]; void permut(mystring_t start,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1442865/slide-24.jpg)



 Вероятностный подход к определению количества информации. Формула Шеннона
Вероятностный подход к определению количества информации. Формула Шеннона Кривые второго порядка на плоскости
Кривые второго порядка на плоскости Решение тригонометрических уравнений
Решение тригонометрических уравнений Методы исследования математических моделей
Методы исследования математических моделей Системы линейных уравнений
Системы линейных уравнений Пересечение поверхностей, метод вспомогательных концентрических сфер
Пересечение поверхностей, метод вспомогательных концентрических сфер Статистический анализ выборок. Числовые характеристики ряда
Статистический анализ выборок. Числовые характеристики ряда Нормальное распределение: свойства и следствия из них
Нормальное распределение: свойства и следствия из них Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Использование равномерной сходимости функциональных последовательностей и рядов
Использование равномерной сходимости функциональных последовательностей и рядов Бариатрия
Бариатрия Модели сложных систем
Модели сложных систем Аттестационная работа. Программа курса по выбору для учащихся 5 класса В мире геометрических фигур
Аттестационная работа. Программа курса по выбору для учащихся 5 класса В мире геометрических фигур Тип игры: викторина Автор: Панфилова Ольга Юрьевна учитель математики МКОУ «Петуховская средняя общеобразовательная школа №1
Тип игры: викторина Автор: Панфилова Ольга Юрьевна учитель математики МКОУ «Петуховская средняя общеобразовательная школа №1 Устный счёт. Транспорт
Устный счёт. Транспорт Многочлен и его стандартный вид
Многочлен и его стандартный вид Вычисление длин дуг. Вычисление объемов тел по площадям поперечных сечений. Вычисление объемов тел вращения. (Лекция 10)
Вычисление длин дуг. Вычисление объемов тел по площадям поперечных сечений. Вычисление объемов тел вращения. (Лекция 10) Тела вращения
Тела вращения Задачи к уроку по теме «Параллелограмм», 8 класс
Задачи к уроку по теме «Параллелограмм», 8 класс Производная функции одной переменной. Введение в математический анализ
Производная функции одной переменной. Введение в математический анализ Рене Декарт
Рене Декарт Вариационный ряд. Полигон, гистограмма
Вариационный ряд. Полигон, гистограмма От проективной геометрии – к неевклидовой (вокруг абсолюта)
От проективной геометрии – к неевклидовой (вокруг абсолюта) Урок № 17 Решение задач по теме трапеция
Урок № 17 Решение задач по теме трапеция Тригонометрический круг
Тригонометрический круг Понятие числа. Числа и операции над ними
Понятие числа. Числа и операции над ними Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Презентация на тему Морской пейзаж
Презентация на тему Морской пейзаж