Содержание
- 2. План 1. Суждения и их виды. Место аксиом и теорем в школьном курсе математики. 2. Теоретические
- 3. Дополнительная рекомендуемая литература Саранцев Г.И. Обучение математическим доказательствам в школе, М.: Просвещение, 2000 Далингер В.А. Методика
- 4. Суждение - форма мышления, в которой что-либо утверждается или отрицается относительно предметов, их свойств и отношений.
- 5. Виды суждений а) по объёму отображаемых предметов: частные и общие б) по качеству отображаемых предметов: утвердительные
- 6. Виды суждений Общеутвердительные Пример: Все квадраты являются прямоугольниками Общеотрицательные Пример: Никакие треугольники не являются квадратами Частноутвердительные
- 7. Формы словесного выражения суждений Категорическая «Вертикальные углы равны» Условная «Если сторона и два прилежащих к ней
- 8. Аксиомы – утверждения, принимаемые без доказательства в данной теории Теоремы – утверждения, истинность которых устанавливается посредством
- 9. Структура теоремы: S – условие, Р – заключение S => P По структуре: простые и сложные
- 10. Виды теорем: 1. Прямая S => P В параллелограмме противоположные углы равны 2. Обратная P =>
- 11. Необходиммые и достаточные условия Если S => Р – истинное высказывание, то Р называют необходимым условием
- 12. Примеры «В параллелограмме противолежащие углы равны» «Четырёхугольник – параллелограмм» - достаточное условия для равенства его противолежащих
- 13. Структура доказательства Тезис – то что нужно доказать Доводы (аргументы) – то, что используется при доказательстве
- 14. Виды доказательств: Прямое Косвенное а) метод от противного б) разделительное доказательство
- 15. Примеры: а) прямое доказательство «В прямоугольнике диагонали равны» Дано: АВСД -прямоугольник Доказать, что АС = ВД
- 16. Примеры: б) косвенное доказательство «Точки, лежащие на прямой, при движении переходят в точки, лежащие на одной
- 17. Примеры: б) косвенное доказательство «Точки, лежащие на прямой, при движении переходят в точки, лежащие на одной
- 18. Воспитание потребности в доказательных рассуждениях осуществляется при использовании Приёмов, показывающих ограниченность опытно-индуктивных обоснований Приёмов, иллюстрирующих эффективность
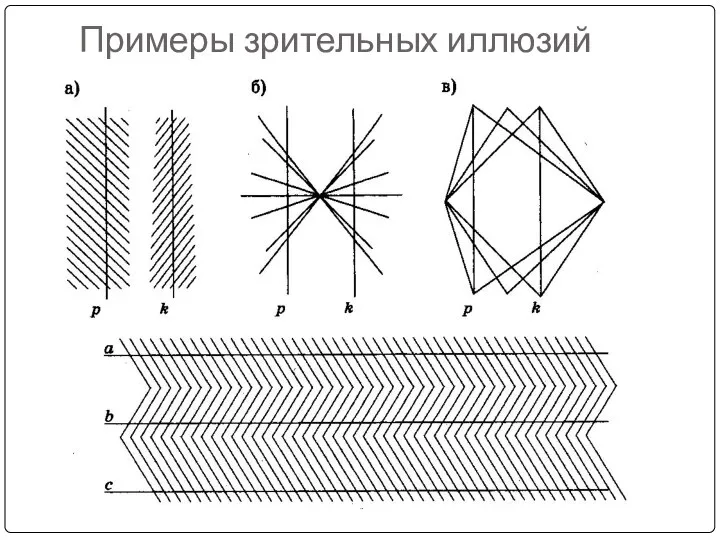
- 19. Примеры зрительных иллюзий
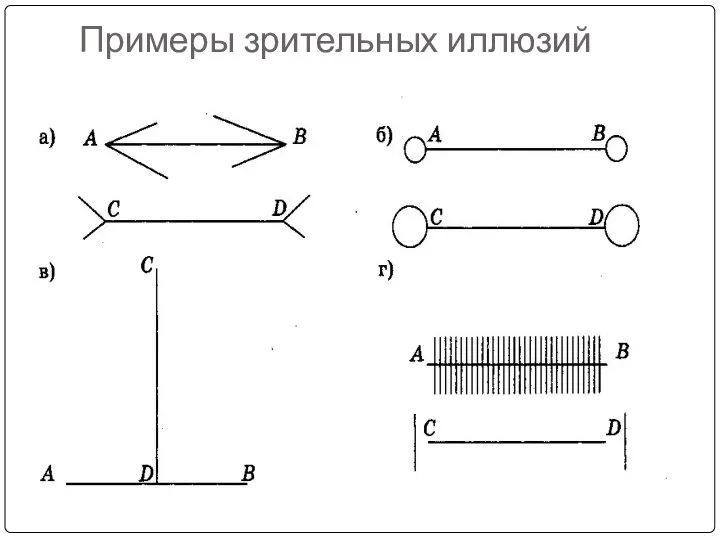
- 20. Примеры зрительных иллюзий
- 21. Примеры упражнений 2-ого вида Верны ли утверждения: а) Все ломаные состоят из трёх звеньев б) Всякий
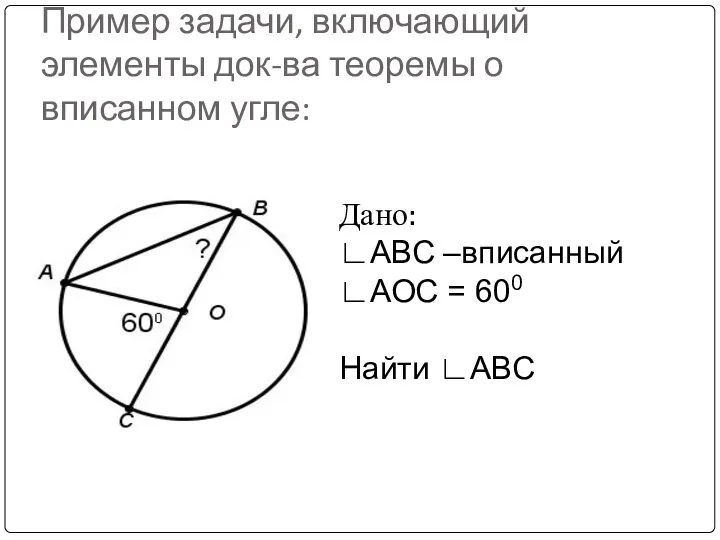
- 22. Пример задачи, включающий элементы док-ва теоремы о вписанном угле: Дано: ∟АВС –вписанный ∟АОС = 600 Найти
- 23. Этапы в изучении теорем Мотивация изучения теоремы Ознакомление с фактом отраженным в теореме Формулирование теоремы, усвоение
- 24. Примеры организации этапов мотивации и раскрытия содержания теоремы Пример 1.: 9 класс, Формула n – ого
- 25. Примеры организации этапов мотивации и раскрытия содержания теоремы Пример 2. 8 класс, теорема о вписанном угле
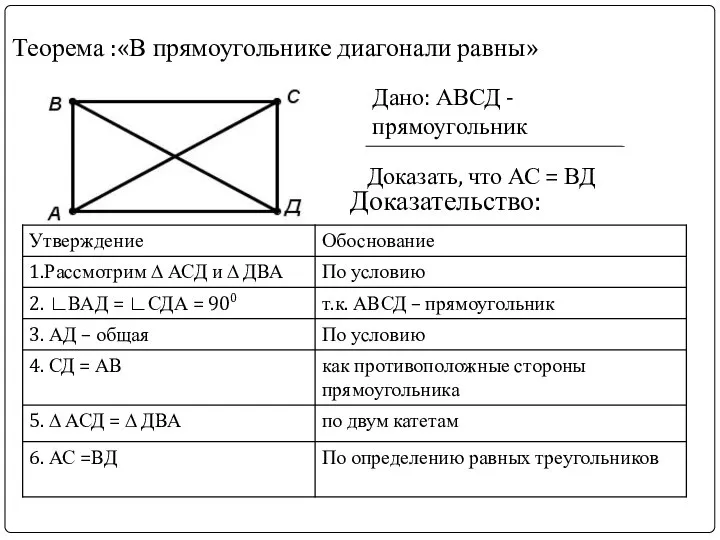
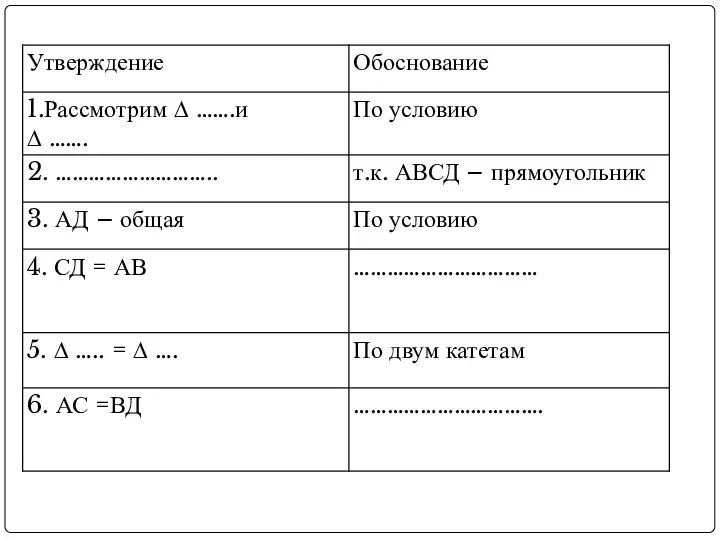
- 26. Теорема :«В прямоугольнике диагонали равны» Дано: АВСД -прямоугольник Доказать, что АС = ВД Доказательство Рассмотрим ∆
- 27. Теорема :«В прямоугольнике диагонали равны» Дано: АВСД -прямоугольник Доказать, что АС = ВД Доказательство:
- 29. Примеры упражнений на усвоение теоремы Для усвоения одного из свойств неравенств можно предложить следующее упражнение: Объясните,
- 31. Скачать презентацию























 Окружность Аполлония
Окружность Аполлония Признаки делимости на 10, на 5 и на 2
Признаки делимости на 10, на 5 и на 2 Алгоритм построения графика квадратичной функции
Алгоритм построения графика квадратичной функции Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Выпуклые четырёхугольники. Специфика параллелограммов. Специфика трапеций
Выпуклые четырёхугольники. Специфика параллелограммов. Специфика трапеций Побудова перерізів многогранників
Побудова перерізів многогранників Сумма бесконечной геометрической прогрессии. Устная работа
Сумма бесконечной геометрической прогрессии. Устная работа Своя игра по математике. Веселые вопросы. Модуль. Математики шутят. Интересные факты
Своя игра по математике. Веселые вопросы. Модуль. Математики шутят. Интересные факты Векторы
Векторы Свойства сложения и умножения Учитель математики и информатики Елисеева З.Х.
Свойства сложения и умножения Учитель математики и информатики Елисеева З.Х. Понятие корреляционной зависимости
Понятие корреляционной зависимости Координаты вектора
Координаты вектора Натуральные числа. Демонстрационный материал
Натуральные числа. Демонстрационный материал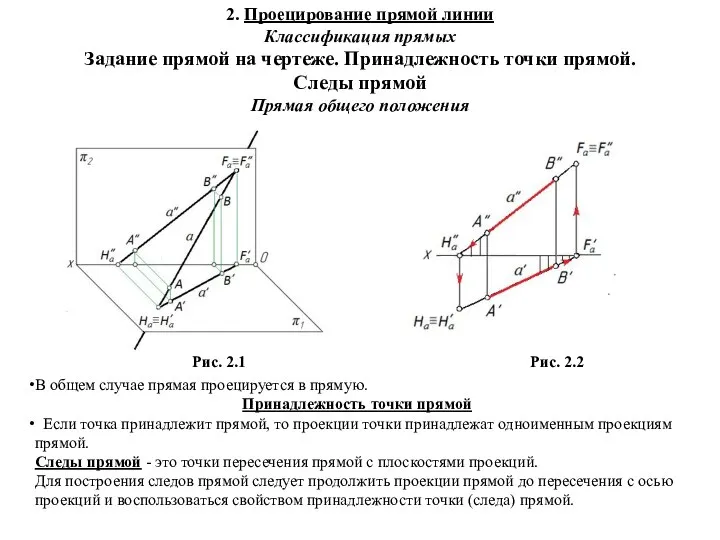 Предмет начертательной геометрии. Проецирование прямой линии. Классификация прямых. Задание прямой на чертеже. (Лекция 2)
Предмет начертательной геометрии. Проецирование прямой линии. Классификация прямых. Задание прямой на чертеже. (Лекция 2) Медианы, высоты, биссектрисы треугольника
Медианы, высоты, биссектрисы треугольника Многогранники
Многогранники Обработка результатов измерений
Обработка результатов измерений Преобразование фигур в пространстве
Преобразование фигур в пространстве Графік квадратичної функції. Тест. 9 клас
Графік квадратичної функції. Тест. 9 клас Медиана, биссектриса и высота треугольника
Медиана, биссектриса и высота треугольника Арксинус. Решение уравнения Sin t = a
Арксинус. Решение уравнения Sin t = a Среднее арифметическое. Проценты
Среднее арифметическое. Проценты Иррациональные уравнения
Иррациональные уравнения МПМ-матрица посадочных лист
МПМ-матрица посадочных лист Задачи на части
Задачи на части Готовимся к ЕГЭ. Комбинация: призма - пирамида
Готовимся к ЕГЭ. Комбинация: призма - пирамида Теорема о точке пересечения высот треугольника
Теорема о точке пересечения высот треугольника Комплексные числа
Комплексные числа