Окружность Аполлония

Сентябрь 12, 2022

Главная
Математика
Окружность Аполлония

Содержание

2. Задача: Что представляет собой множество точек плоскости, отношение расстояний от которых до двух данных точек есть
3. Решение получилось очень сложное – поскольку применены геометрические приемы. Однако в работах французского математика Рене Декарта
4. . Итак, пусть даны две точки ,А и В и некоторое положительное число k, равное отношению
5. Тогда получим следующие координаты точек: В(0,0), А(a,0), М(x,y). Пусть a=3 опять для простоты рассуждений.
6. Тогда, пользуясь формулами расстояния между двумя точками, запишем:
7. Получили уравнение окружности с центром в точке (-1;0) и радиусом r=2. Значение радиуса не случайно вспомним,
8. Решая задачу в общем виде т.е. при условии ,что точка А имеет координаты (a;0) и k≠1
9. Пусть теперь k ≠ 1. имеем и условие принадлежности точки M искомому множеству можно записать в
11. Скачать презентацию

Слайд 2

Задача: Что представляет собой множество точек плоскости, отношение расстояний от которых

до двух данных точек есть величина постоянная?

Решение: Впервые эту задачу сформулировал и решил Аполлоний Пергский, (260-170 гг. до н.э.)

Слайд 3

Решение получилось очень сложное – поскольку применены геометрические приемы. Однако в

работах французского математика Рене Декарта эта задача решена более элегантно. Декарт применил метод координат.

Слайд 4

. Итак, пусть даны две точки ,А и В и некоторое

положительное число k, равное отношению расстояний до точки М.
1случай. Если k=1,тогда множество точек М есть серединный перпендикуляр к отрезку АВ.
2 случай. Пусть k целое не отрицательное число не равное 1
Для удобства решения возьмем k=2 , т.е. МА: МВ=2.
Введем систему прямоугольных координат. Совместим начало отсчета с точкой В. В качестве положительной полуоси x возьмем луч ВА.

Слайд 5

Тогда получим следующие координаты точек: В(0,0), А(a,0), М(x,y). Пусть a=3 опять

для простоты рассуждений.

Слайд 6

Тогда, пользуясь формулами расстояния между двумя точками, запишем:

Слайд 7

Получили уравнение окружности с центром в точке (-1;0) и радиусом r=2.
Значение

радиуса не случайно вспомним, что мы выбрали k=2.

Слайд 8

Решая задачу в общем виде т.е. при условии ,что точка А

имеет координаты (a;0) и k≠1 получим уравнение окружности в виде:

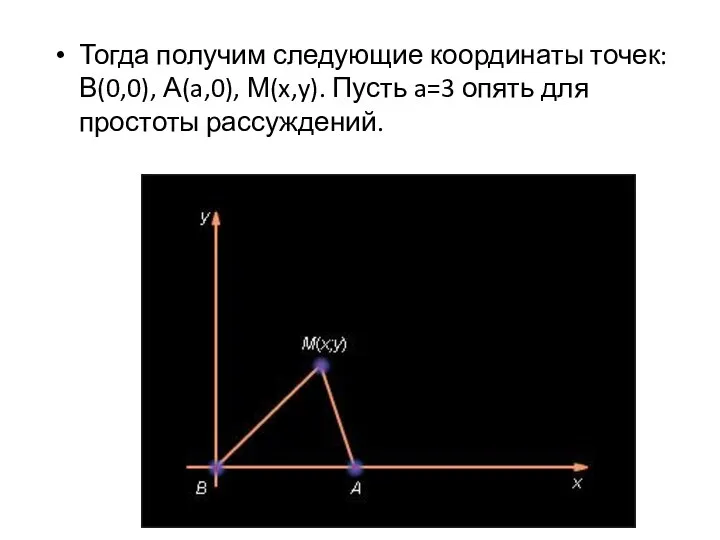
В данной системе координат точка B имеет координаты (0; 0), а точка A – (a; 0), где a > 0. Пусть M (x, y) – произвольная точка, удовлетворяющая условию задачи, то есть AM = k · BM, где k – заданное положительное число. Если k = 1, то это означает, что искомое множество состоит из точек, равноудаленных от данных точек A и B. Из свойств серединного перпендикуляра к отрезку следует, что искомым множеством в этом случае будет прямая, проходящая через середину отрезка AB перпендикулярно оси OX.

Слайд 9