Содержание
- 2. Из истории появления понятия «группа» 1771 г. – изучал группы Sn ≈ 1831 – термин «группа»
- 3. https://www.rulit.me/author/dalma-a/evarist-galua-revolyucioner-i-matematik-get-475922.html http://pyrkov-professor.ru/default.aspx?tabid=190&ArticleId=764
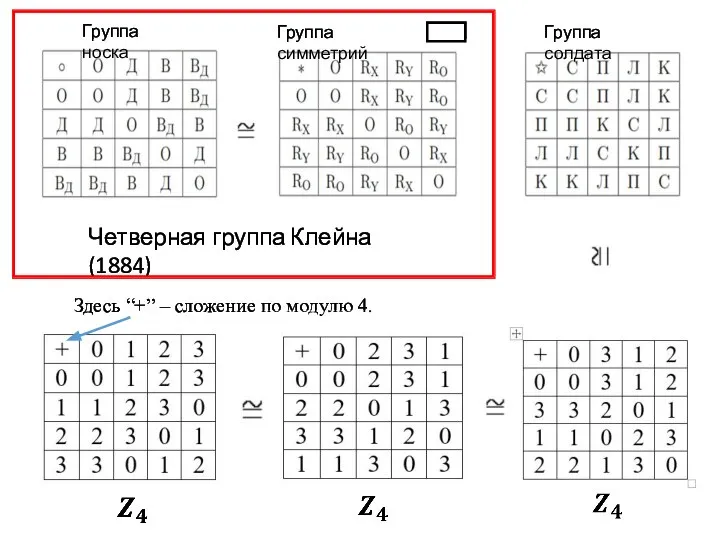
- 4. Четверная группа Клейна (1884) Здесь “+” – сложение по модулю 4.
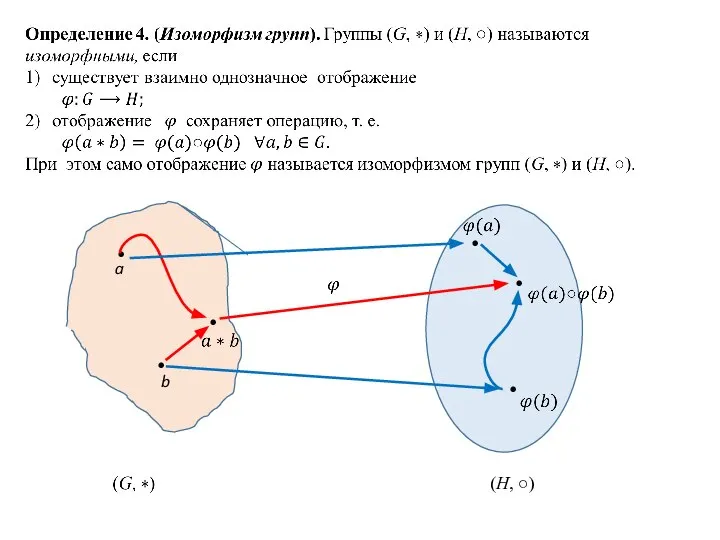
- 5. (H, ○) • • • • • • a b
- 6. Доказательство.
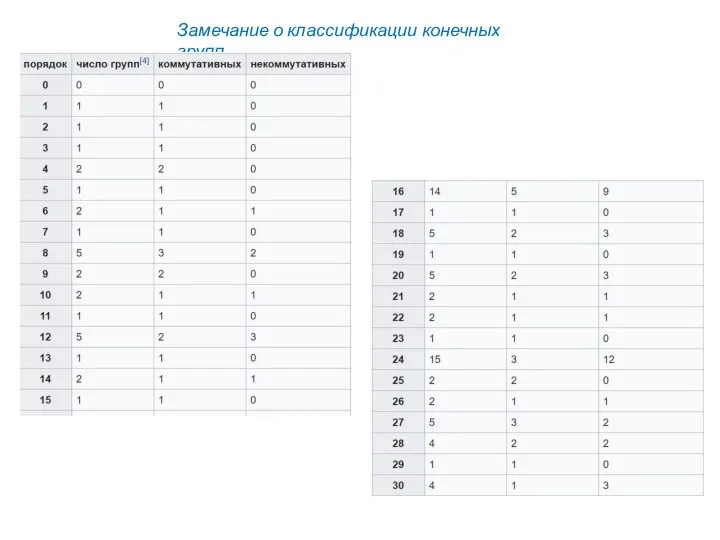
- 7. Замечание о классификации конечных групп
- 8. Теорема классификации утверждает, что список конечных простых групп состоит из 18 счётных бесконечных семейств, плюс 26
- 9. Однако проверку перечисленных условий можно заменить проверкой одного условия: Доказательство. Очевидно, поскольку по условию H –
- 10. Из критерия подгруппы легко следует утверждение, которое Вам предлагается для самостоятельного доказательства: Замечание: в аддитивной записи
- 11. Доказательство легко вытекает из определения степени и из обобщённой ассоциативности. в частности, Это утверждение непосредственно следует
- 12. Примеры. Таким образом, циклическая группа, порождённая матрицей А, имеет порядок 2. Таким образом, теперь подгруппа, порождённая
- 13. 8. –
- 15. Скачать презентацию









 Окружность. Длина окружности
Окружность. Длина окружности Приемы реализации деятельностного подхода на уроках математики
Приемы реализации деятельностного подхода на уроках математики Сложение обыкновенных дробей. Устно для 6 кл
Сложение обыкновенных дробей. Устно для 6 кл Степень числа. Квадрат и куб числа
Степень числа. Квадрат и куб числа Занимательная математика. Игры с кубиками (1 класс)
Занимательная математика. Игры с кубиками (1 класс) Геометрический смысл производной
Геометрический смысл производной Математическая логика и теория алгоритмов. Введение. (Глава 1)
Математическая логика и теория алгоритмов. Введение. (Глава 1) Аттестационная работа. Методическая разработка по выполнению проектной работы «Как измерить удава»
Аттестационная работа. Методическая разработка по выполнению проектной работы «Как измерить удава»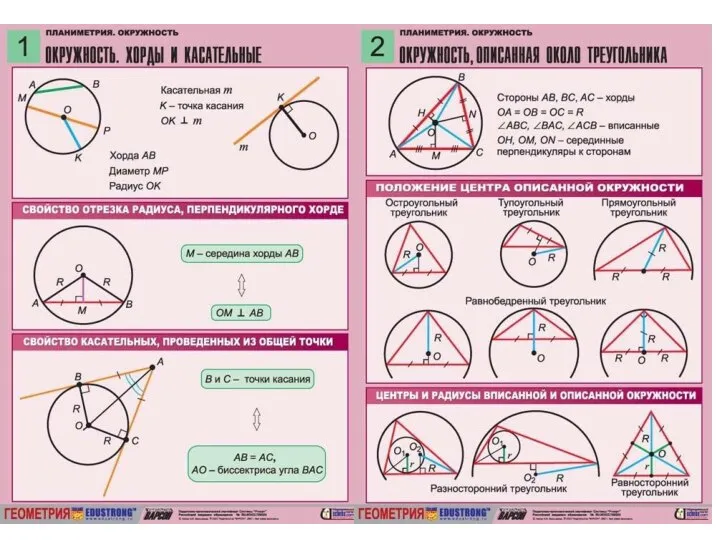 Геометрия. Конспекты
Геометрия. Конспекты Степени и корни
Степени и корни Из истории математики
Из истории математики Задания В9
Задания В9 Устные способы решения квадратных уравнений. 8 класс
Устные способы решения квадратных уравнений. 8 класс Задачи с параметром. Аналитический способ
Задачи с параметром. Аналитический способ Обходы. Эйлеров и гаильтонов графы
Обходы. Эйлеров и гаильтонов графы Золотое сечение
Золотое сечение Признаки равенства треугольников
Признаки равенства треугольников Степень с отрицательным показателем
Степень с отрицательным показателем Матрицы. Обозначение матриц
Матрицы. Обозначение матриц Презентация по математике "Соблюдение грамматических норм: незначительность или необходимость?" - скачать
Презентация по математике "Соблюдение грамматических норм: незначительность или необходимость?" - скачать  Производная функции
Производная функции Простейшие тригонометрические неравенства. Неравенство cos x < a
Простейшие тригонометрические неравенства. Неравенство cos x < a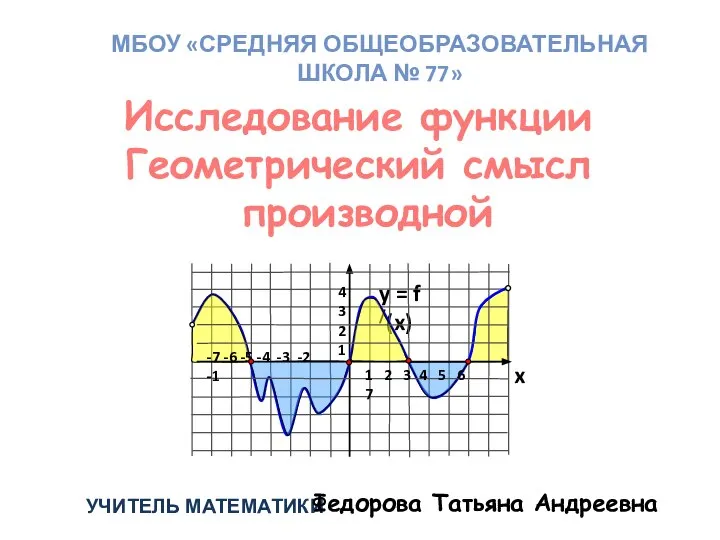 Исследование функции. Геометрический смысл производной
Исследование функции. Геометрический смысл производной Лекция 2. Кривые поверхности
Лекция 2. Кривые поверхности Системы счисления. Арифметические действия над систематическими числами
Системы счисления. Арифметические действия над систематическими числами Введение в методы статистического анализа многомерных объектов
Введение в методы статистического анализа многомерных объектов Подготовка к ЕГЭ, ГИА. Задачи на часы
Подготовка к ЕГЭ, ГИА. Задачи на часы Язык геометрических рисунков
Язык геометрических рисунков