Содержание
- 2. Матрицы Матрицей порядка m × n называют прямоугольную таблицу чисел (вещественных или комплексных), содержащую m строк
- 3. Перестановки Всякое расположение чисел 1, 2,..., n в некотором определенном порядке называется перестановкой из n чисел
- 4. Определители Пусть А - квадратная матрица порядка n. Определителем этой матрицы называется алгебраическая сумма всевозможных произведений
- 5. Свойства определителя I. Если все элементы какой-либо строки (столбца) определителя равны нулю, то он равен нулю.
- 6. Вычисление определителя Рекуррентная формула 1 Минором Мij элемента аij матрицы A порядка n называется определитель матрицы
- 7. Вычисление определителя Рекуррентная формула 2 Метод элементарных преобразований столбцов Выделяем строку i, в котором мы хотим
- 12. Операции над матрицами. Линейные операции Операция сложения - возможна только для матриц одинаковой размерности Складываются элементы
- 13. Операции над матрицами. Транспонирование матриц При транспонировании строки и столбцы матрицы меняются местами Меняется размерность неквадратной
- 14. Операции над матрицами. Умножение матриц Умножение матриц – возможно, если число столбцов матрицы А равно числу
- 15. Умножается каждая строка матрицы слева на каждый столбец матрицы справа Обозначим: r1 r2 – строки матрицы
- 18. 799 802
- 20. Операции над матрицами. Единичная матрица. Обратная матрица Диагональная матрица (квадратная), у которой все диагональные элементы равны
- 21. Операции над матрицами. Обращение матриц Минором Мij элемента аij матрицы A порядка n называется определитель матрицы
- 22. Операции над матрицами. Обращение матрицы Процедура нахождения обратной матрицы: . Составляем матрицу А* = (а *ij)
- 27. Составляем матрицу n × 2n : (A E) В нашем распоряжении элементарные операции со строками 1)
- 30. Скачать презентацию














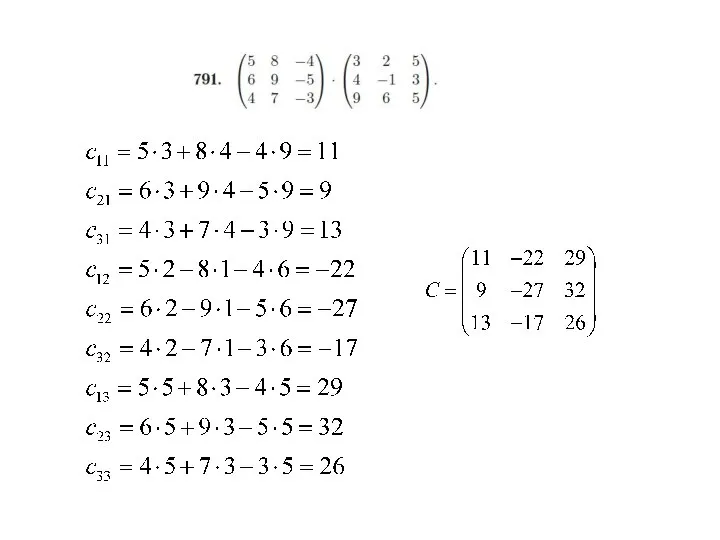

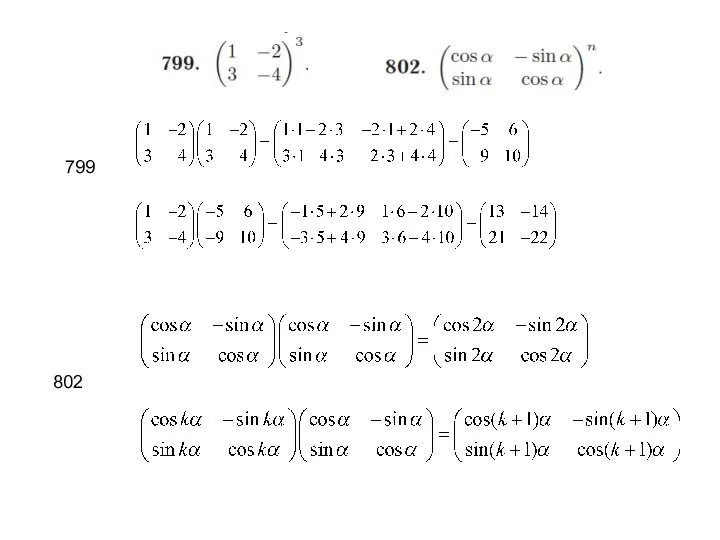






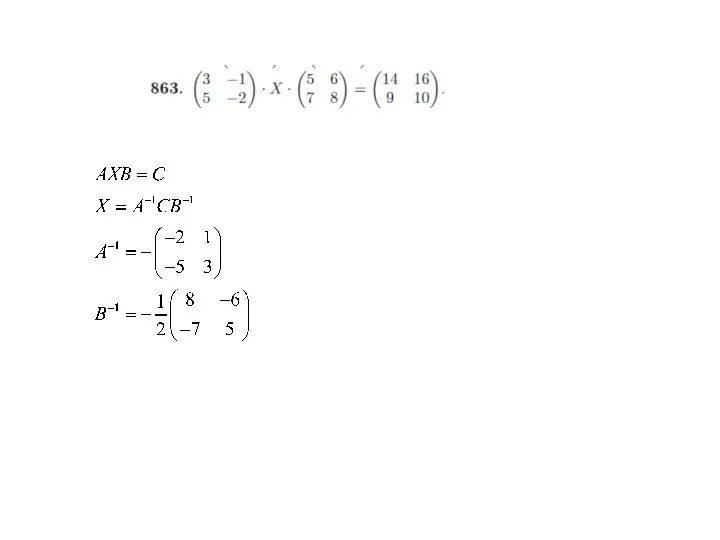
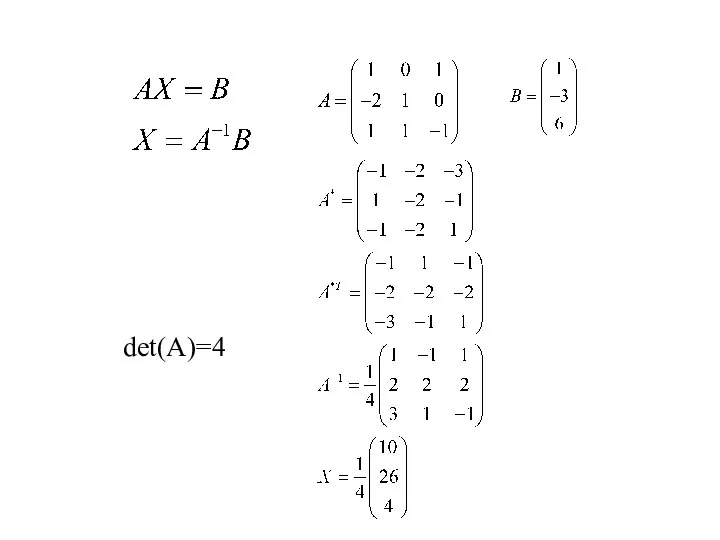


 Логические задачи 1 класс - Презентация_
Логические задачи 1 класс - Презентация_ Равнобедренный треугольник
Равнобедренный треугольник Четырехугольники. Параллелограмм. Геометрия 8 класс
Четырехугольники. Параллелограмм. Геометрия 8 класс Составные высказывания
Составные высказывания Многоугольники. Подготовка к ЕГЭ
Многоугольники. Подготовка к ЕГЭ Волшебные превращения геометрических фигур (ИЗО, 1 класс)
Волшебные превращения геометрических фигур (ИЗО, 1 класс) Урок математики в 4 классе: «Единицы массы. Тонна. Центнер.» Михайлова Н.А. Учитель высшей категории МОАУ СОШ №15 г. Орска, Оре
Урок математики в 4 классе: «Единицы массы. Тонна. Центнер.» Михайлова Н.А. Учитель высшей категории МОАУ СОШ №15 г. Орска, Оре Кластерный анализ. Практическое занятие №3
Кластерный анализ. Практическое занятие №3 Простые геометрические фигуры
Простые геометрические фигуры Формулы Крамера для решения системы линейных алгебраических уравнений с невырожденной квадратной матрицей
Формулы Крамера для решения системы линейных алгебраических уравнений с невырожденной квадратной матрицей Подобие правильных выпуклых многоугольников
Подобие правильных выпуклых многоугольников Общие методы решения тригонометрических уравнений
Общие методы решения тригонометрических уравнений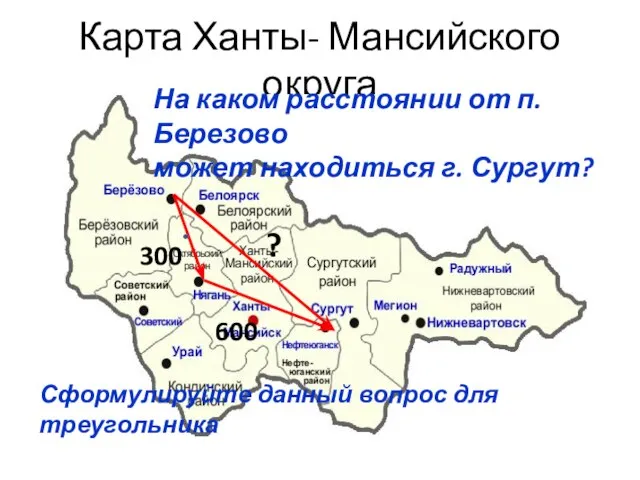 Неравенство треугольника
Неравенство треугольника Аттестационная работа. Методическая разработка Проектноисследовательская деятельность учащихся на уроках математики
Аттестационная работа. Методическая разработка Проектноисследовательская деятельность учащихся на уроках математики Correlation Regression
Correlation Regression Решение квадратных уравнений
Решение квадратных уравнений Прямая пропорциональность и её график
Прямая пропорциональность и её график Прямые и плоскости в пространстве. Тема 2
Прямые и плоскости в пространстве. Тема 2 Основные понятия теории чисел. Лекция 9
Основные понятия теории чисел. Лекция 9 Сложение и вычитание десятичных дробей. Урок с использованием интерактивной доски
Сложение и вычитание десятичных дробей. Урок с использованием интерактивной доски Презентация по математике "Тренажёр таблицы умножения и деления" - скачать бесплатно
Презентация по математике "Тренажёр таблицы умножения и деления" - скачать бесплатно Презентация на тему Определенный интеграл
Презентация на тему Определенный интеграл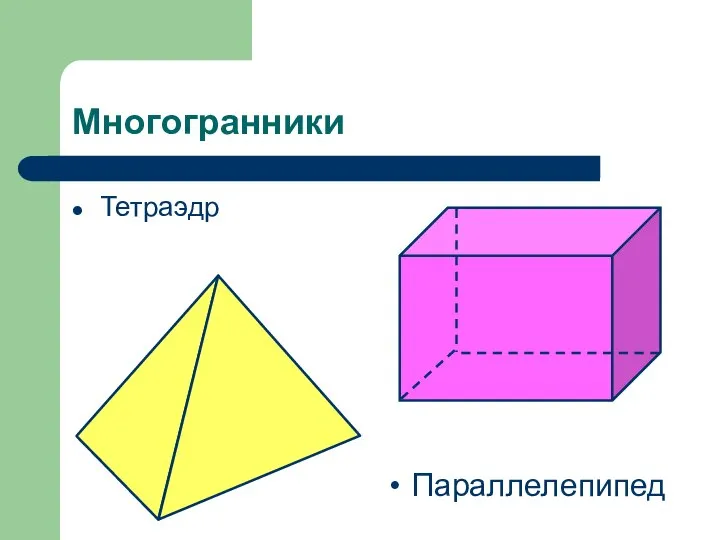 Многогранники
Многогранники Площади. Подготовка к ЕГЭ
Площади. Подготовка к ЕГЭ Измерение углов
Измерение углов Отрицательные целые числа
Отрицательные целые числа Интеграл и его практическое применение
Интеграл и его практическое применение Игровые технологии на уроках математики
Игровые технологии на уроках математики