Содержание
- 2. CONTEÚDO PROGRAMÁTICO DESTA AULA Equações diferenciais de 1a ordem Método de Euler
- 3. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Uma Equação Diferencial Ordinária (EDO) é uma equação da forma F(x, y(x), y’(x),
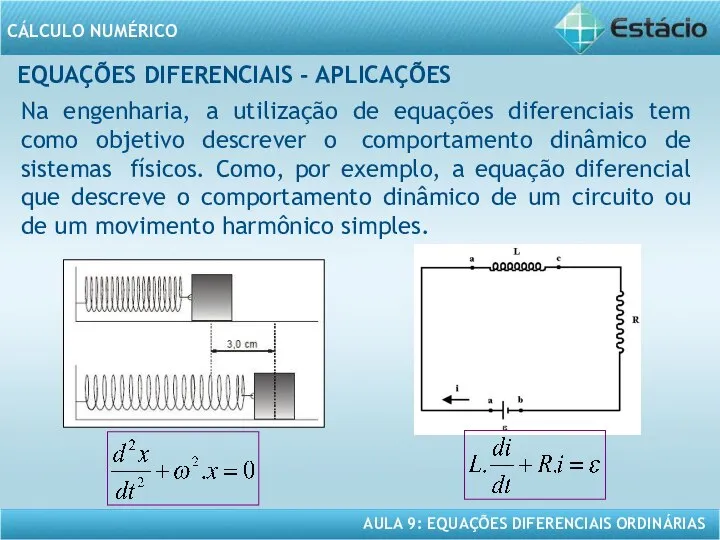
- 4. EQUAÇÕES DIFERENCIAIS - APLICAÇÕES Na engenharia, a utilização de equações diferenciais tem como objetivo descrever o
- 5. EQUAÇÕES DIFERENCIAIS - CONCEITOS A ordem da equação diferencial é a ordem da mais alta derivada
- 6. SOLUÇÃO DE UMA EQUAÇÃO DIFERENCIAL A solução de uma equação diferencial é uma função que não
- 7. PROBLEMA DE VALOR INICIAL (PVI) Para que a equação diferencial tenha solução única define-se o PVI
- 8. EXEMPLO 1. Dada a equação diferencial y’’ + 4y = 0, verifique se y = C1.cos2x
- 9. EXEMPLO 1 - CONTINUAÇÃO. y = C1.cos2x + C2.sen2x e y’ = -2C1.sen2x + 2C2.cos2x y(π/4)
- 10. MÉTODO DE EULER O método de Euler, também conhecido como método da reta secante, é um
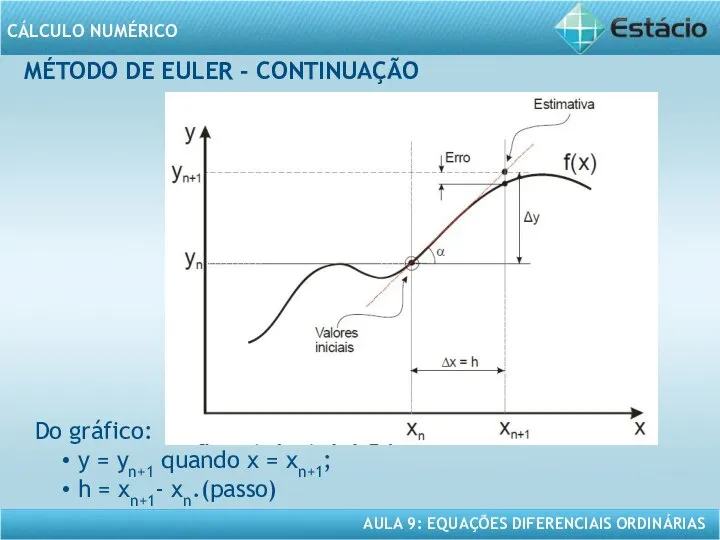
- 11. MÉTODO DE EULER - CONTINUAÇÃO Do gráfico: y = yn+1 quando x = xn+1; h =
- 12. MÉTODO DE EULER - CONTINUAÇÃO Equação da reta: yn+1 = yn + tgα. (xn+1- xn) tgα
- 13. EXEMPLO 2 – Resolva a equação y’ = 1 – x + 4y com a condição
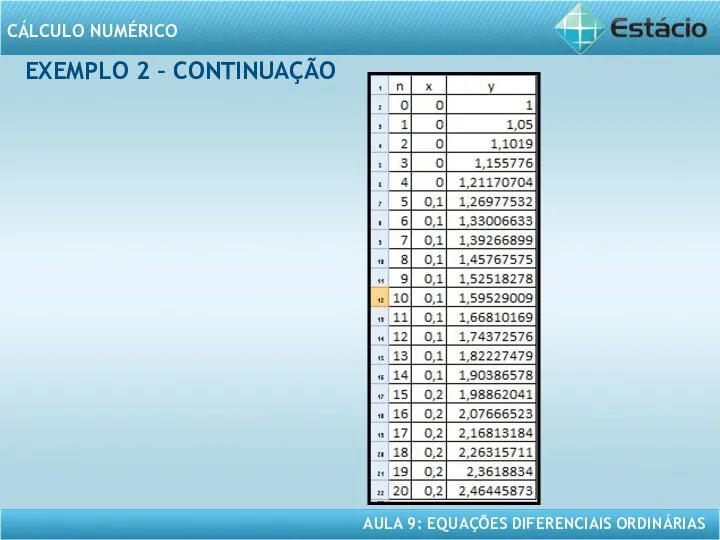
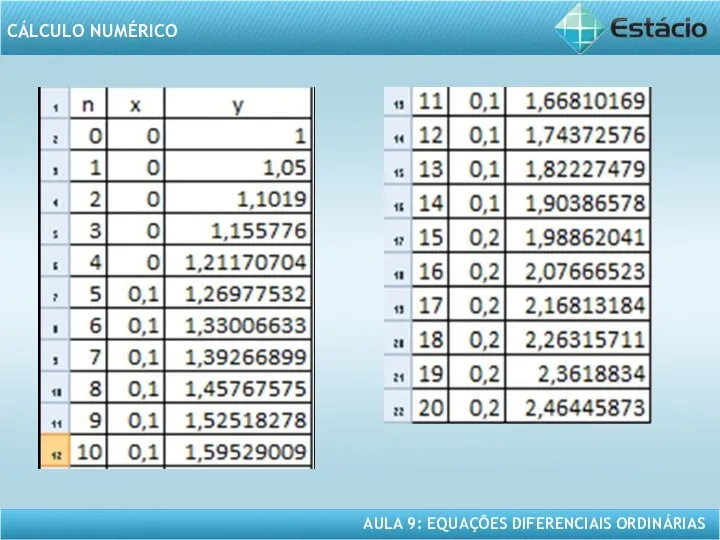
- 14. EXEMPLO 2 – CONTINUAÇÃO Solução yn+1 = yn + h.f(xn,yn) ⇒ yn+1 = yn + 0,01.(1
- 15. EXEMPLO 2 – CONTINUAÇÃO
- 18. Скачать презентацию











 Өлшеу шкалалары
Өлшеу шкалалары Математический час «Это интересно знать!»
Математический час «Это интересно знать!» Проверка домашнего задания
Проверка домашнего задания Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Числа - близнецы
Числа - близнецы Я вырасту здоровым. Занимательная математика. Вторая младшая группа
Я вырасту здоровым. Занимательная математика. Вторая младшая группа Площадь параллелограмма, треугольника, трапеции
Площадь параллелограмма, треугольника, трапеции Решение линейных уравнений. 7класс Автор: Богданова Н.Ю., учитель математики МОУ СОШ №7, г.Губкинский, ЯНАО.
Решение линейных уравнений. 7класс Автор: Богданова Н.Ю., учитель математики МОУ СОШ №7, г.Губкинский, ЯНАО.  Объем прямой призмы
Объем прямой призмы Лекция 4. Основы математической статистики
Лекция 4. Основы математической статистики Решение планиметрических задач
Решение планиметрических задач Решение простейших задач по теории вероятности
Решение простейших задач по теории вероятности Сумма углов треугольника
Сумма углов треугольника Зимняя сказка. Игра – тренажёр. 1 – 2 класс
Зимняя сказка. Игра – тренажёр. 1 – 2 класс Решение задач с помощью линейных уравнений
Решение задач с помощью линейных уравнений Радианная мера угла
Радианная мера угла Определители II и III порядка. Их свойства и вычисление
Определители II и III порядка. Их свойства и вычисление Формулы. Закрепление применения формул при решении задач
Формулы. Закрепление применения формул при решении задач Соотношение между сторонами и углами прямоугольного треугольника (задачи по готовым чертежам)
Соотношение между сторонами и углами прямоугольного треугольника (задачи по готовым чертежам) Презентация на тему Координатная плоскость»(6 класс)
Презентация на тему Координатная плоскость»(6 класс)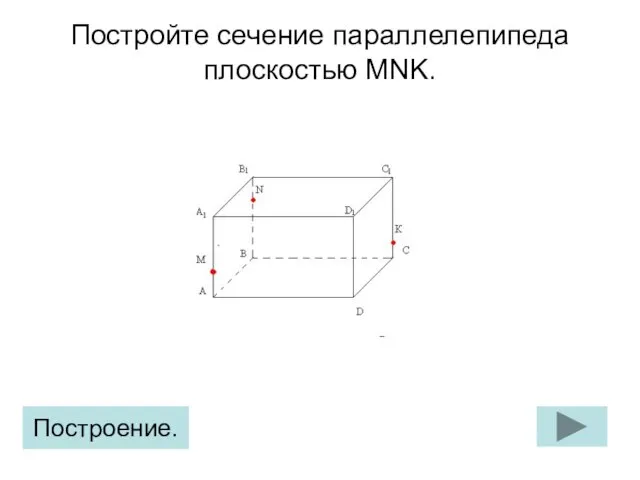 Параллелепипед. Построение сечения (задание 6)
Параллелепипед. Построение сечения (задание 6) Решение заданий №6 (трапеция) по материалам открытого банка задач ЕГЭ по математике 2016 года
Решение заданий №6 (трапеция) по материалам открытого банка задач ЕГЭ по математике 2016 года Математический каламбур. Анаграммы в стихах
Математический каламбур. Анаграммы в стихах Основы теории множеств
Основы теории множеств Квадратные неравенства с параметрами
Квадратные неравенства с параметрами Алгебра 08.04.2020
Алгебра 08.04.2020 Изучение отношений в курсе геометрии основной школы
Изучение отношений в курсе геометрии основной школы Расстояние от точки до фигуры
Расстояние от точки до фигуры