Содержание
- 2. Основные понятия Множество – совокупность определенных различаемых объектов, причем таких, что для каждого можно установить, принадлежит
- 3. Основные понятия Множества могут быть конечными, бесконечными и пустыми. Множество, содержащее конечное число элементов, называется конечным.
- 4. Основные понятия Множество ? называют подмножеством множества ? (обозначается ?⊆?), если всякий элемент множества ? является
- 5. Основные понятия Множества ? и ? равны (?=?) тогда и только тогда, когда ?⊆?, и ?⊆?,
- 6. Основные понятия
- 7. Способы задания множеств Задание множеств списком предполагает перечисление элементов. Пример: A={a, b , c , d}
- 8. Способы задания множеств Пример: B={b⏐b=π/2±kπ, k∈N0}, N0 – множество всех натуральных чисел; M2n=1, 2, 4, 8,
- 9. Способы задания множеств Так, «множество всех хороших песен 2013 года» каждый составит по-разному. Надежным способом однозначного
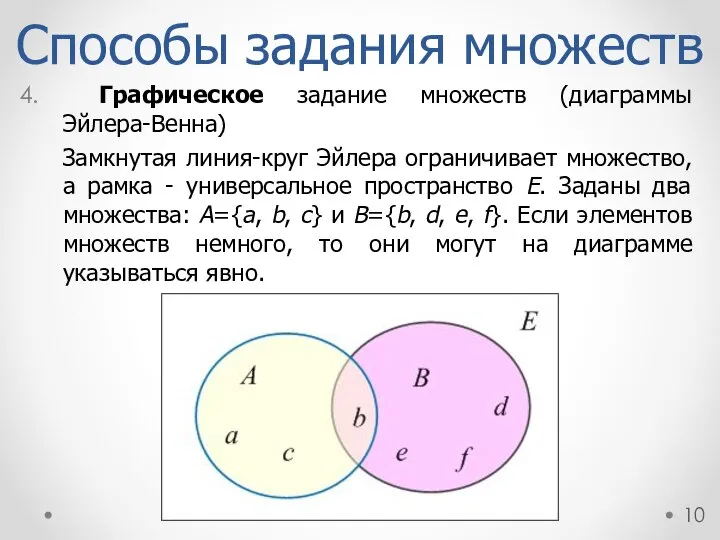
- 10. Способы задания множеств Графическое задание множеств (диаграммы Эйлера-Венна) Замкнутая линия-круг Эйлера ограничивает множество, а рамка -
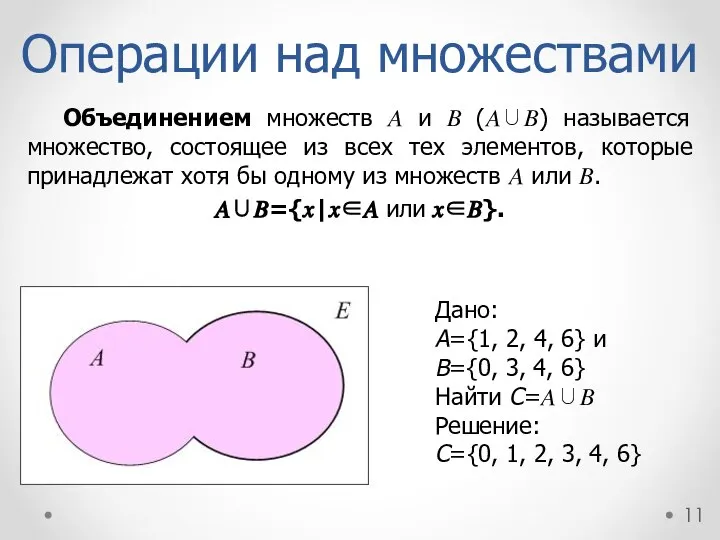
- 11. Операции над множествами Объединением множеств ? и ? (?∪?) называется множество, состоящее из всех тех элементов,
- 12. Операции над множествами Пересечением множеств A и B (A∩B) называется множество, состоящее из элементов, входящих как
- 13. Операции над множествами Разностью множеств A и B (A\B) называется множество всех элементов множества A, которые
- 14. Операции над множествами Симметричная разность множеств A и B (AΔB) AΔB=(A∪B)\(A∩B) Дано: A={1, 2, 4, 6}
- 15. Операции над множествами Приоритет выполнения операций: дополнение, затем пересечение и только потом объединение и разность.
- 16. § 9. Основы теории графов
- 17. Основные понятия Теория графов - мощное средство исследования и решения многих задач, возникающих при изучении больших
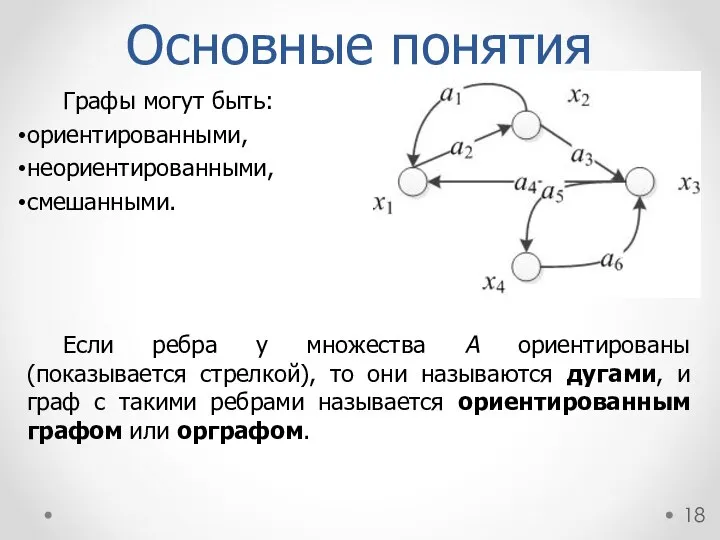
- 18. Основные понятия Графы могут быть: ориентированными, неориентированными, смешанными. Если ребра у множества A ориентированы (показывается стрелкой),
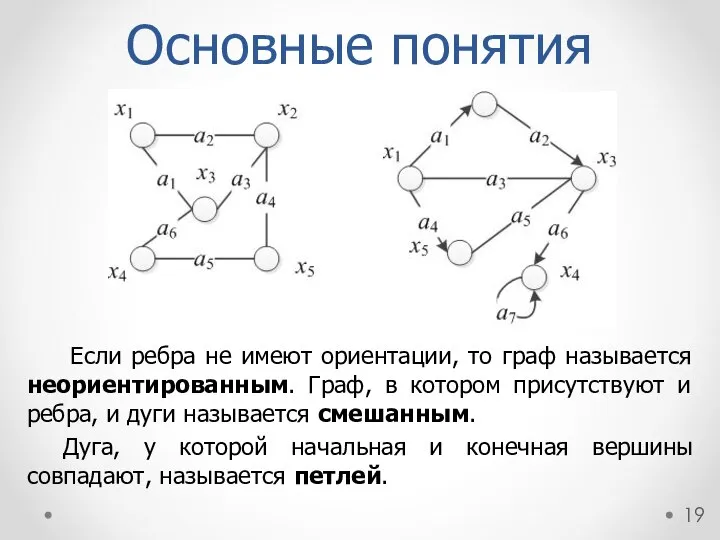
- 19. Основные понятия Если ребра не имеют ориентации, то граф называется неориентированным. Граф, в котором присутствуют и
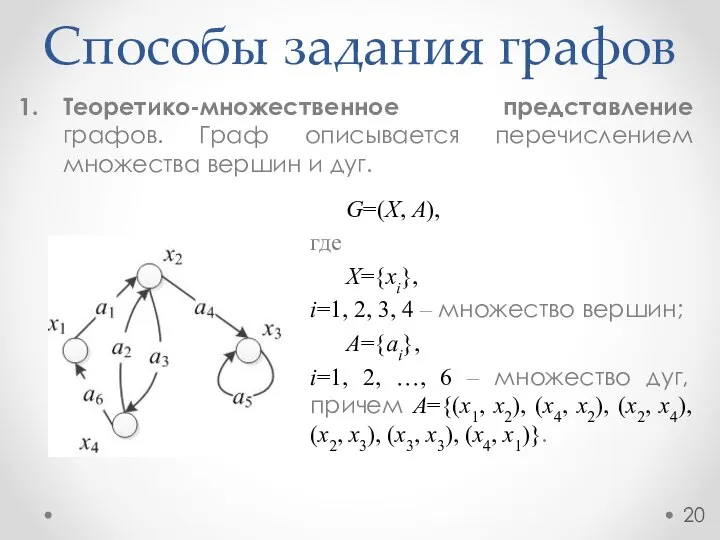
- 20. Способы задания графов Теоретико-множественное представление графов. Граф описывается перечислением множества вершин и дуг. G=(X, A), где
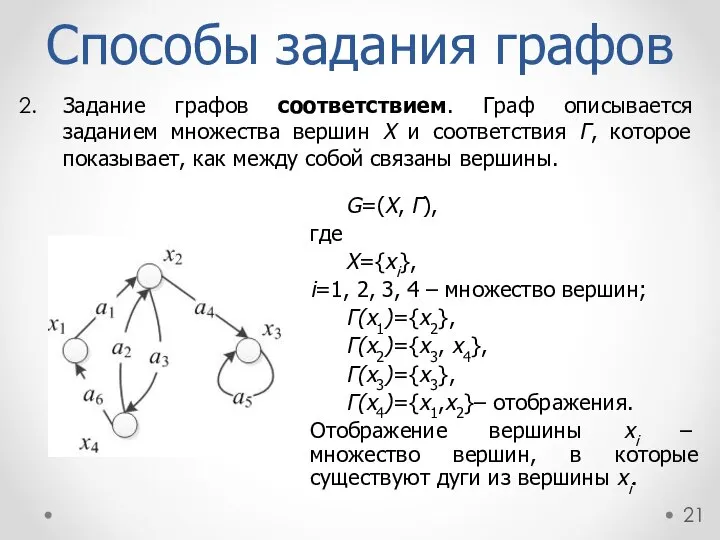
- 21. Способы задания графов Задание графов соответствием. Граф описывается заданием множества вершин Х и соответствия Г, которое
- 22. Способы задания графов
- 23. Способы задания графов 3.2. Матрица инциденций представляет собой прямоугольную матрицу размером n x m, где n
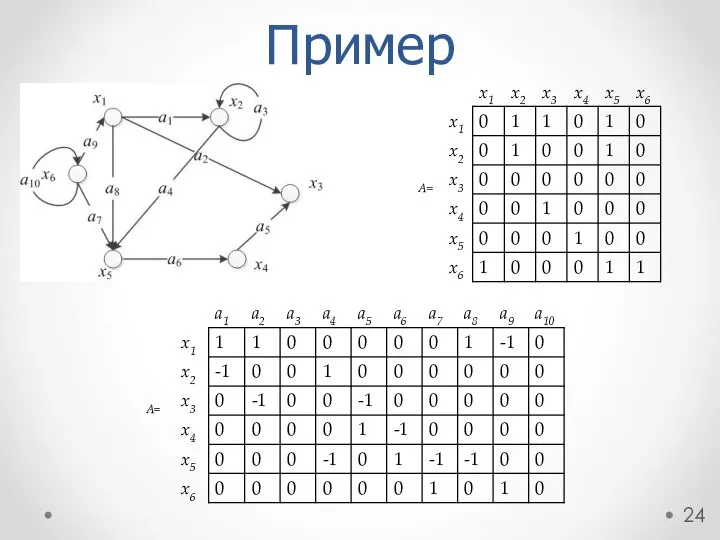
- 24. Пример
- 25. Структура графа Дан граф ?=(?, ?). Подграф - граф ?’=(?’, ?’), полученный из исходного удалением части
- 26. Структура графа Вершина ? называется достижимой из вершины ?, если существует маршрут из ? в ?.
- 27. Задача Березовое: 8:00 Полевое Б 16:00 07:30 11:50 14:00 14:40 16:10
- 28. Методы обхода графа Под обходом графа понимается перебор его вершин в определенном порядке, связанный с проходом
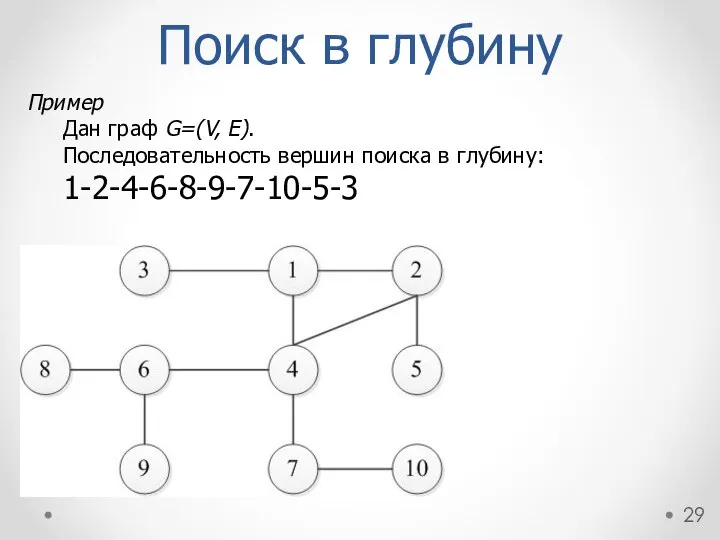
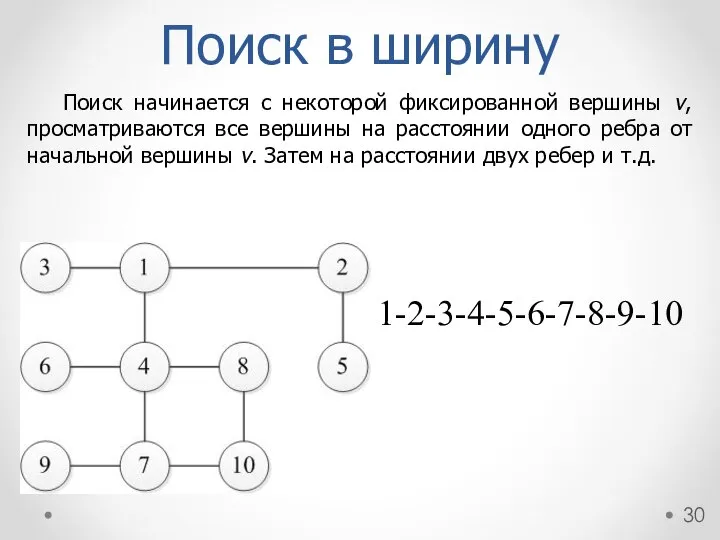
- 29. Пример Дан граф G=(V, E). Последовательность вершин поиска в глубину: 1-2-4-6-8-9-7-10-5-3 Поиск в глубину
- 30. Поиск начинается с некоторой фиксированной вершины v, просматриваются все вершины на расстоянии одного ребра от начальной
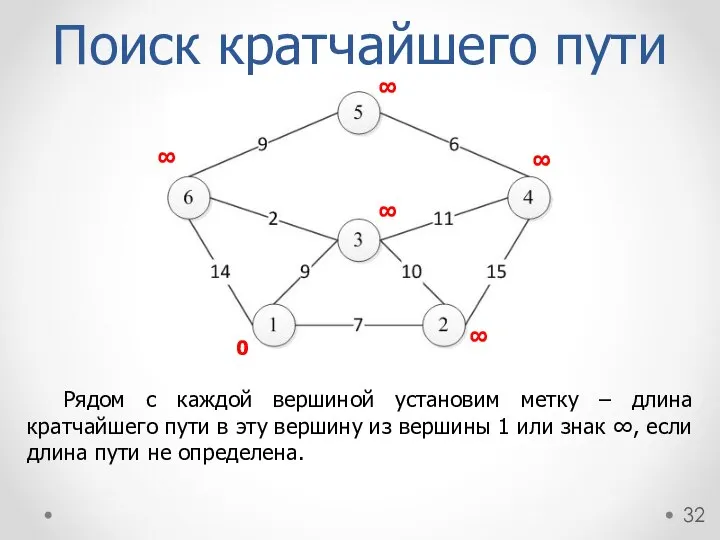
- 31. Граф G=(V, E) называется взвешенным, если каждому ребру v поставлено в соответствие некоторое число, называемое его
- 32. Рядом с каждой вершиной установим метку – длина кратчайшего пути в эту вершину из вершины 1
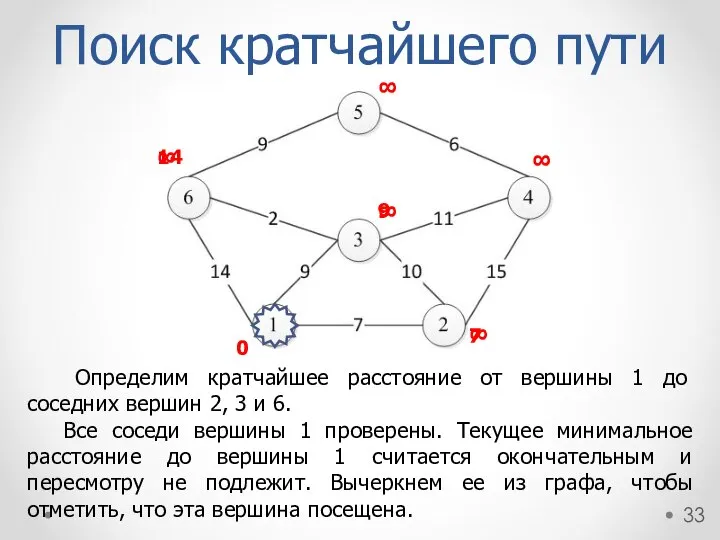
- 33. Определим кратчайшее расстояние от вершины 1 до соседних вершин 2, 3 и 6. Все соседи вершины
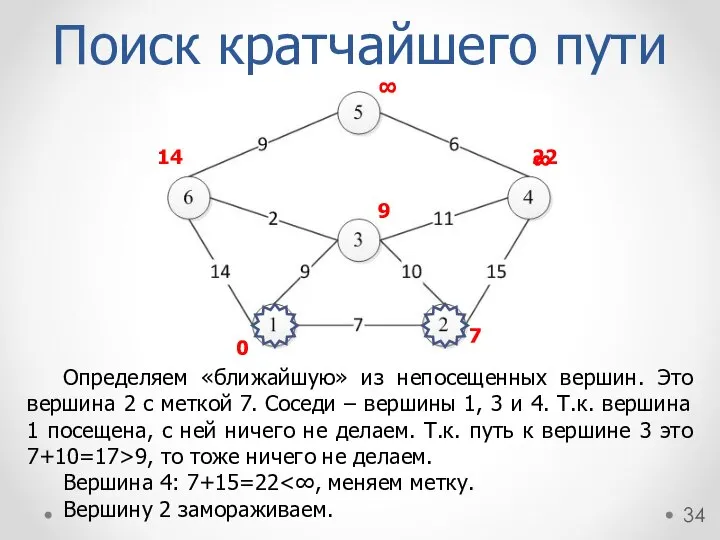
- 34. Определяем «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7. Соседи – вершины 1, 3
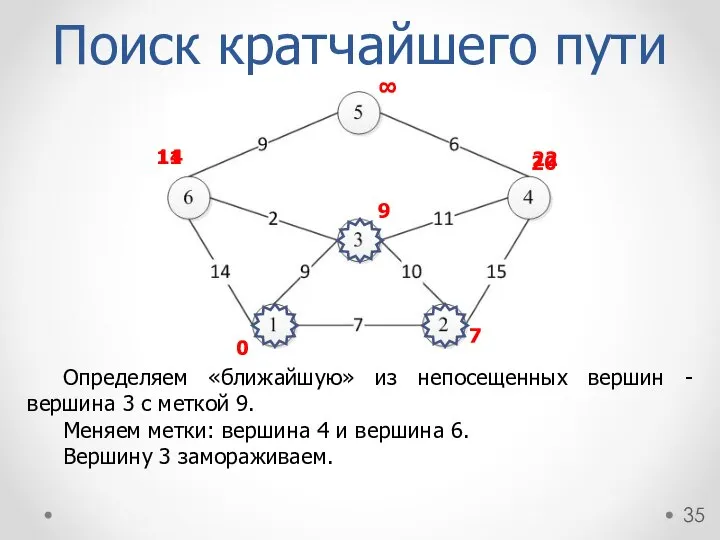
- 35. Определяем «ближайшую» из непосещенных вершин - вершина 3 с меткой 9. Меняем метки: вершина 4 и
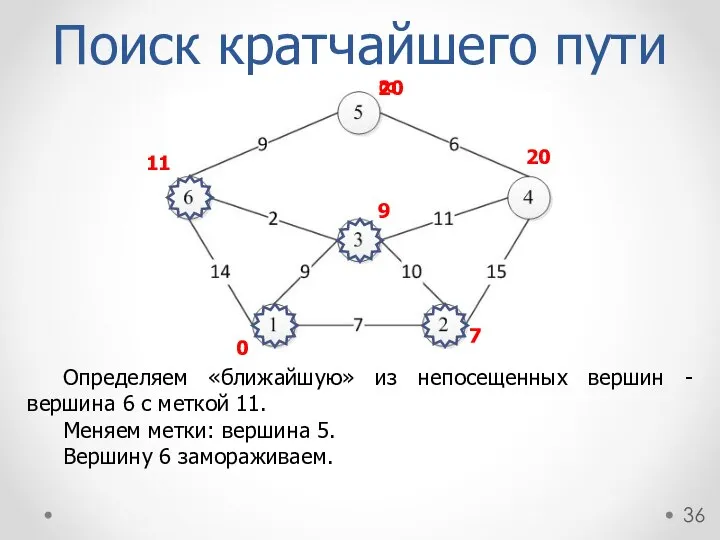
- 36. Определяем «ближайшую» из непосещенных вершин - вершина 6 с меткой 11. Меняем метки: вершина 5. Вершину
- 38. Скачать презентацию





















 Площади фигур
Площади фигур Скрещивающиеся прямые
Скрещивающиеся прямые Сложение и вычитание десятичных дробей. Путешествие в сказку
Сложение и вычитание десятичных дробей. Путешествие в сказку Славянская нумерация
Славянская нумерация Этапы расчета прогнозных значений с помощью корреляционно-регрессионного анализа (однофакторная модель)
Этапы расчета прогнозных значений с помощью корреляционно-регрессионного анализа (однофакторная модель) Решение системы способом подстановки. 7 класс
Решение системы способом подстановки. 7 класс Округление дробей
Округление дробей GEOMETRIYa_povtorenie
GEOMETRIYa_povtorenie Центральные и вписанные углы. 8 класс
Центральные и вписанные углы. 8 класс Решение задач с помощью пропорции Автор презентации: Козаева Сима Сергеевна учитель математики ЦО №1828 «Сабурово» г. Москв
Решение задач с помощью пропорции Автор презентации: Козаева Сима Сергеевна учитель математики ЦО №1828 «Сабурово» г. Москв МОУ СОШ №256 г.Фокино Приморский край. Каратанова Марина Николаевна.
МОУ СОШ №256 г.Фокино Приморский край. Каратанова Марина Николаевна.  Вписанная окружность
Вписанная окружность  Теоремы ТЗ
Теоремы ТЗ Обучающий тест ГИА
Обучающий тест ГИА МБОУ «Хабарская СОШ № 1» Проект «Неделя математики» Выполнили: ученики 7 «А» класса Антюхин Владимир, Варига Олеся, Кривенко Анн
МБОУ «Хабарская СОШ № 1» Проект «Неделя математики» Выполнили: ученики 7 «А» класса Антюхин Владимир, Варига Олеся, Кривенко Анн Ряды. Числовые ряды
Ряды. Числовые ряды Геометрический смысл двойного интеграла
Геометрический смысл двойного интеграла Теорема Пифагора
Теорема Пифагора Расстояние между точкой и прямой
Расстояние между точкой и прямой Функциональная грамотность. Математическая грамотность
Функциональная грамотность. Математическая грамотность Властивості паралельних прямих. 7 клас
Властивості паралельних прямих. 7 клас Цилиндр
Цилиндр Связь между координатами векторов и координатами точек
Связь между координатами векторов и координатами точек Число и цифра
Число и цифра Интерактивный тренажер «Котёнок Гав». Математика 1 класс. Связь между суммой и слагаемыми
Интерактивный тренажер «Котёнок Гав». Математика 1 класс. Связь между суммой и слагаемыми Математика на палочках
Математика на палочках Презентация по математике "Вокруг света с математикой" - скачать
Презентация по математике "Вокруг света с математикой" - скачать  Число пи
Число пи