Числовые, функциональные и степенные ряды

Числовым рядом называется сумма вида:

где числа u1, u2, u3,…,un,... – члены

Если или ,
то ряд называется сходящимся, а число S – суммой

Пример.

Найти сумму членов ряда:

Находим частичные суммы членов ряда:

Запишем последовательность частичных сумм: …

Общий член этой последовательности есть: n/(2n+1)

Последовательность частичных

Необходимый признак сходимости ряда

Ряд может сходиться только при условии, что его

Достаточные признаки сходимости ряда с положительными членами

а) Признак сравнения рядов с

образован из членов геометрической прогрессии:

Геометрический ряд

сходится при |q|<1

расходится при |q|≥1

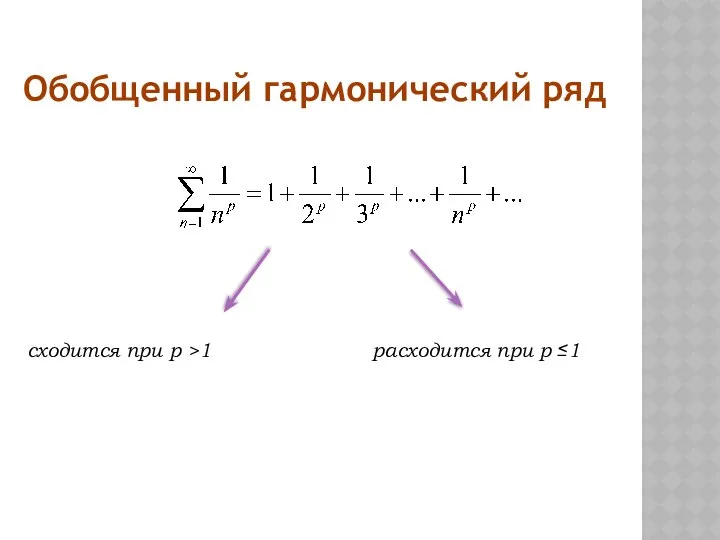
Обобщенный гармонический ряд

сходится при p >1

расходится при p ≤1

Пример. Исследовать сходимость ряда, применяя необходимый признак сходимости и признак сравнения:

Необходимый

Сравнивая члены нашего ряда с соответствующими членами геометрического ряда, получим неравенства:

Т.е.

Пример. Исследовать сходимость ряда, используя признак Даламбера:

Следовательно, данный ряд сходится.

ОСНОВНЫЕ ПОНЯТИЯ

Определение 1:
Функциональным называется ряд, члены которого есть непрерывные функции от

ПРИМЕР ФУНКЦИОНАЛЬНОГО РЯДА

Рассмотрим геометрическую прогрессию со знаменателем х:
.
Геометрическая

ОСНОВНЫЕ ПОНЯТИЯ

Определение 2:
Совокупность значений x, при которых ФР сходится, называется областью

Определение 3:
ФР называется равномерно сходящимся в некоторой области X, если для

Определение 4:
Пусть даны:
причем в некоторой области выполняется условие:
Тогда

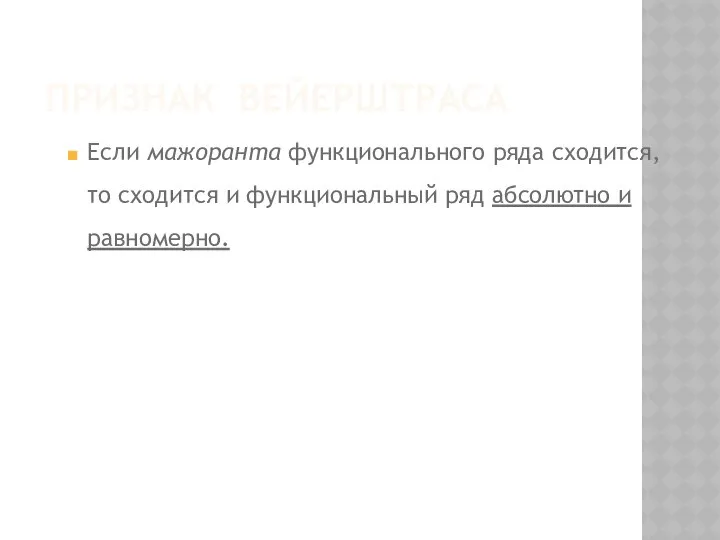
ПРИЗНАК ВЕЙЕРШТРАСА

Если мажоранта функционального ряда сходится, то сходится и функциональный ряд

СВОЙСТВА АБСОЛЮТНО И РАВНОМЕРНО СХОДЯЩИХСЯ РЯДОВ

Пусть даны функциональные ряды:

СТЕПЕННЫЕ РЯДЫ

Определение 5:
Функциональный ряд вида:
называется степенным рядом.

ТЕОРЕМА АБЕЛЯ

Если степенной ряд сходится при x = x1, то он

НАХОЖДЕНИЕ РАДИУСА СХОДИМОСТИ

По признаку Даламбера:

НАХОЖДЕНИЕ РАДИУСА СХОДИМОСТИ

По радикальному признаку Коши:

РЯД ТЕЙЛОРА

Определение 6:
Рядом Тейлора функции f(x) называется степенной ряд вида:
это есть

ДОСТАТОЧНОЕ УСЛОВИЕ РАЗЛОЖЕНИЯ ФУНКЦИИ В РЯД ТЕЙЛОРА

Определение 6:
Всякая функция f(x) бесконечно

РЯД МАКЛОРЕНА

Определение 7:
Рядом Маклорена функции f(x) называется степенной ряд вида:
это есть

СТЕПЕННЫЕ РЯДЫ

Определение. Ряд
называется степенным по степеням х . Ряд

ИНТЕРВАЛ СХОДИМОСТИ СТЕПЕННОГО РЯДА

Для любого степенного ряда существует конечное неотрицательное

НАХОЖДЕНИЕ ИНТЕРВАЛА СХОДИМОСТИ ПО ПРИЗНАКУ ДАЛАМБЕРА

Составим ряд из абсолютных величин

ПРОДОЛЖЕНИЕ

В этом случае ряд будет сходиться внутри интервала (-R,R),где R-это

ПРИМЕРЫ

Найти интервал сходимости ряда
.
Следовательно, ряд сходится абсолютно в

ПРИМЕРЫ

Положим . Тогда получим числовой ряд . Этот ряд расходится

ПРИМЕРЫ

Найти интервал сходимости степенного
ряда . Здесь ,
=

ПРОДОЛЖЕНИЕ
= .
Но 0<1 всегда, т.е. независимо от x. Это

ПРИМЕР

Найти интервал сходимости ряда .
= =
= = .

СВОЙСТВА СТЕПЕННЫХ РЯДОВ. НЕПРЕРЫВНОСТЬ СУММЫ РЯДА

1. Сумма степенного ряда

ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ

2. Ряд, полученный почленным дифференцированием степенного ряда, является

ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ

3. Степенной ряд можно почленно интегрировать на любом промежутке,

ОПРЕДЕЛЕНИЯ

Определение. Если бесконечно дифференцируемая функция является суммой степенного ряда, то

СТЕПЕННОЙ РЯД КАК РЯД ТЕЙЛОРА

Теорема. Если в некоторой окрестности точки

ФОРМУЛА ТЕЙЛОРА

Рассмотрим n-ю частичную сумму ряда Тейлора:
Этот многочлен называется

ФОРМУЛА ТЕЙЛОРА С ОСТАТОЧНЫМ ЧЛЕНОМ В ФОРМЕ ЛАГРАНЖА

Остаточный член в

УСЛОВИЯ СХОДИМОСТИ РЯДА ТЕЙЛОРА К ФУНКЦИИ У=F(X)

Для того чтобы функцию

ДОСТАТОЧНЫЕ УСЛОВИЯ РАЗЛОЖИМОСТИ ФУНКЦИИ В РЯД ТЕЙЛОРА

Если функция f(x) на

РАЗЛОЖЕНИЕ

Все производные этой функции совпадают с самой функцией, а в

РАЗЛОЖЕНИЕ В РЯД СИНУСА.

Вычислим производные синуса:

ПРОДОЛЖЕНИЕ

Ясно, что все производные синуса не превосходят по модулю единицу.

ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ

Разложения 1–7 позволяют, используя соответствующее разложение, вычислять приближенно

РЕШЕНИЕ

Разложим подынтегральную функцию в степенной ряд:

ПРОДОЛЖЕНИЕ
Так как получившийся ряд является знакочередующимся, то сумма знакочередующегося ряда не

ПРОДОЛЖЕНИЕ

Вычислив еще несколько членов ряда
видим, что
Отбросив этот