Делимость натуральных чисел

Замечание:

Вопрос о существовании разности на множестве натуральных чисел решается очень просто:

Для операции деления такого
простого признака нет.
Поэтому и возникла в математике

Определение отношения делимости натуральных чисел

Пусть даны натуральные числа a и b.

Говорят,

b называют делителем числа a, число a – кратным b

Обозначают

Читают :

Что общего и что различного в понятиях?
1. «делитель данного числа»
2.

24 : 5 - число 5 есть делитель. Компонент действия

Уточним понятие «отношение делимости»

1. Единица (число 1) является делителем любого натурального

Доказательство:
Так как

, то существует такое

, что a = b·g

Значит,

Следствие:

Множество делителей данного числа конечно.
Например:
Делители числа 36 образуют конечное множество

Сопутствующие понятия Простые и составные числа

Определение:
Простым числом называется такое натуральное число, большее

Например:

Число 7 – простое.
Число 2 – простое.
(единственное простое четное число).
Числа

Определение:
Составным числом называется натуральное число, которое имеет более двух делителей.
Например:

Чисел кратных данному числу, бесконечное множество.
Например:
Числа кратные 6 образуют множество:

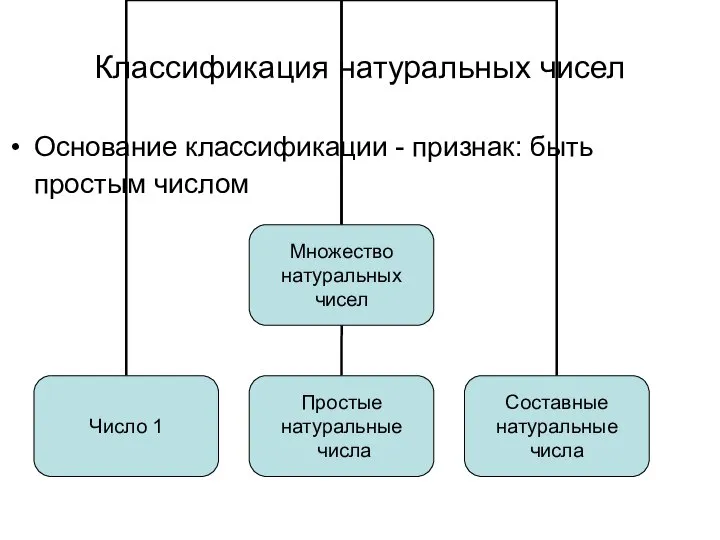
Классификация натуральных чисел

Основание классификации - признак: быть простым числом

Свойства отношения делимости

1. Отношение делимости рефлексивно, антисимметрично и транзитивно.
2. Отношение делимости

Теорема 1.

Отношение делимости рефлексивно.
(любое натуральное число делится само на себя).
Если отношение

Доказательство

Для любого натурального a
справедливо равенство a=a·1.

по определению делимости

Что и требовалось

Теорема 2

Отношение делимости антисиммет-рично (если a кратно b, то b не

Доказательство: (доказательство осуществляется методом от противного)

Предположим обратное.
Пусть

но тогда a ≤

Теорема 3

Отношение делимости транзитивно.

Если отношение делимости
обозначить –R, а элементы отношения

Доказательство

Если

, то

такое, что

a = b · g

Если

, то

такое, что

Тогда

Признак делимости суммы Теорема 4

Если каждое из натуральных чисел

делится на натуральное число

Доказательство

Если

то

Если

то

- - - - - - - -

Преобразуем сумму чисел

Так как сумма натуральных чисел есть натуральное число, то

Замечание

Обратная теорема: если сумма натуральных чисел кратна натуральному числу c, то

Признак делимости разности Теорема 5

Если уменьшаемое a и вычитаемое b делятся на

Обобщение теоремы 5

Теорема:
Разность двух натуральных чисел a и b

Краткое условие теоремы

Дано: a>b и

Доказать, что

Доказательство

Рассмотрим разность чисел a и b.

Следовательно, (a-b) кратно с

Например:

Задание: Не выполняя вычислений, определите делится ли разность чисел 247 и162

Признак делимости произведения Теорема 6

Если число a делится на b, то произведение

Доказательство

Так как

, то

Умножим обе части этого равенства

Следствие:

Если один из множителей произведения делится на натуральное число, то и

Еще три теоремы о делимости

Теорема 1
Если в сумме одно слагаемое

Доказательство

Пусть

И известно, что

Доказательство проведем методом
«от противного»

Предположим противное.
Пусть

Преобразуем сумму s

Имеем:

Применим теорему о делимости разности.

Следовательно:

Противоречие

Значит наше предположение

Теорема 2. (задача)
Если в произведении a·b множитель a делится на натуральное

Теорема 3.
Если произведение a·c делится на произведение b·c, причем c-натуральное число,

Доказательство

Так как

Значит

ассоциативный