Содержание
- 2. Вопрос 1. Логарифмическое дифференцирование Пусть у = lnu, где u = φ(х) - дифференцируемая функция. Применяя
- 3. Таким образом, имеем или (1) Производная называется логарифмической производной функции u = φ(х).
- 4. О.1.1. Операция, состоящая в последовательном применении к функции сначала логарифмирования (по основанию е), а затем дифференцирования,
- 5. Найдем производную данной функции логарифмическим дифференцированием: lny = vlnu. Отсюда по формуле (1) получим откуда
- 6. Подставив у = uv, получим или Замечание Производная степенно-показательной функции состоит из двух слагаемых. Первое слагаемое
- 7. Логарифмическое дифференцирование может быть применено для отыскания производных не только степенно-показательных функций, но и таких, непосредственное
- 8. Пример 1. Найти у′, если Решение Прологарифмируем данную функцию: Отсюда Если воспользоваться выражением (1), то получится
- 9. Пример 2. Найти у′, если Решение Прологарифмируем данную функцию: Умножая на у и подставляя его значение,
- 10. Вопрос 2. Дифференцирование функций, заданных неявно 2.1. Неявное задание функции О.2.1.Если функция задана уравнением у =
- 11. Всякую явно заданную функцию у = f(х) можно записать как неявно заданную уравнением у ‒ f(х)
- 12. Пример 3. х2 + у2 = 1 - неявная функция ⇒ Не всегда легко, а иногда
- 13. 2.2. Дифференцирование неявных функций Пусть неявная функция у задана уравнением (2) F(x,y) = 0, не разрешенным
- 14. Пример 5. Найти производную функции у, заданной уравнением х3 + у3 ‒ 3ху = 0. Решение
- 15. Вопрос 3. Дифференцирование функций, заданных параметрически 3.1. Параметрическое задание функции О.3.1.Параметрическим заданием функции у = f(х)
- 16. Пример 6. 1) 2) Здесь 0 ≤ t ≤ 2π.
- 17. 3.2. Дифференцирование функций, заданных параметрически Пусть зависимость между аргументом х и функцией у задана параметрически в
- 18. Пример 7. Пусть . Найти у′х. Решение
- 19. Вопрос 4. Производные высших порядков Производная у′ = f′(х) функции у = f(х) есть так же
- 20. Таким образом О.4.2. Производная от второй производной функции у = f(х) называется производной третьего порядка или
- 21. Производные, начиная со второй, называются производными высших порядков. О.4.3. Производная от (n‒1)-й производной функции у =
- 22. Начиная с производной 4-го порядка, производные обозначают римскими цифрами или числами в скобках. Пример 8. уV
- 23. Пример 9. Найти производную n-го порядка функции у = ах. Решение
- 24. Механический (физический) смысл второй производной Пусть материальная точка движется прямолинейно по закону S = S(t). Известно,
- 25. 4.2. Производные высших порядков неявных функций Пусть неявная функция у задана уравнением (2), т.е. F(x,y) =
- 26. Пример 10. Найти у‴, если х2 + у2 = 1. Решение F(x,y) = 0 ⇒ х2
- 27. 4.3. Производные высших порядков от функций, заданных параметрически Пусть функция у = f(х) задана параметрически в
- 28. Найдем вторую производную от функции, заданной параметрически. Из определения второй производной и равенства (4) следует, что
- 30. Скачать презентацию
















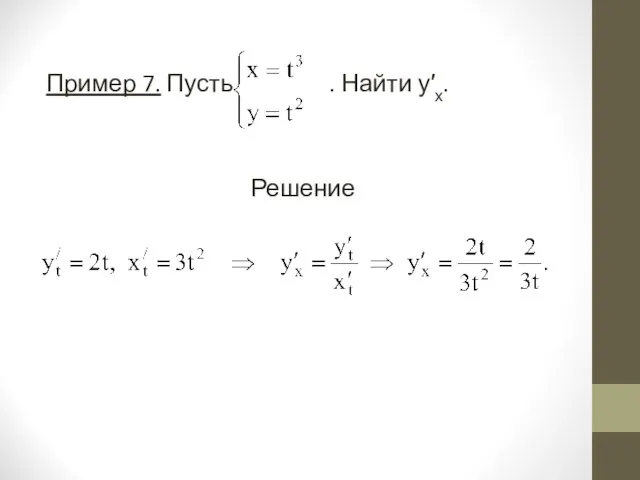










 Предел функции в точке
Предел функции в точке Площадь пряиоугольного треугольника
Площадь пряиоугольного треугольника Состав числа 5
Состав числа 5 Урок математики 3 класс (3 четверть) Тема : «Деление суммы на число» Учитель : Буряк Светлана Владимировна МОУ Ступ
Урок математики 3 класс (3 четверть) Тема : «Деление суммы на число» Учитель : Буряк Светлана Владимировна МОУ Ступ Упрощение выражений. 5 класс
Упрощение выражений. 5 класс Стандартный вид числа Урок-путешествие вокруг Земли Алгебра, 9 класс Учитель математики МОУ «СОШ №8» г. Канаш ЧР ХАЛИУ
Стандартный вид числа Урок-путешествие вокруг Земли Алгебра, 9 класс Учитель математики МОУ «СОШ №8» г. Канаш ЧР ХАЛИУ Разложение многочлена на множители способом группировки
Разложение многочлена на множители способом группировки Математический язык
Математический язык Золотое сечение Работу выполняла: ученица6а класса Богачёва Валя
Золотое сечение Работу выполняла: ученица6а класса Богачёва Валя  Чисельні методи. Елементи теорії похибок. (Лекція 1)
Чисельні методи. Елементи теорії похибок. (Лекція 1) Обобщающий урок по теме «Соотношения между сторонами и углами треугольника»
Обобщающий урок по теме «Соотношения между сторонами и углами треугольника» Площади четырехугольников и треугольников
Площади четырехугольников и треугольников Искусственный интеллект – наука и технология создания интеллектуальных машин
Искусственный интеллект – наука и технология создания интеллектуальных машин Равнобедренный треугольник. Геометрия 7 класс
Равнобедренный треугольник. Геометрия 7 класс Матрицы и СЛАУ МНК. (Лекция 5 )
Матрицы и СЛАУ МНК. (Лекция 5 ) Перетворення графіків функцій
Перетворення графіків функцій Римские цифры Выполнила обучающаяся 6 класса МОУ «Краснопресненская СОШ им. В.П.Дмитриева» Гунбетова Карина Преподаватель: Па
Римские цифры Выполнила обучающаяся 6 класса МОУ «Краснопресненская СОШ им. В.П.Дмитриева» Гунбетова Карина Преподаватель: Па Отражение истории развития алгебры в современных учебниках
Отражение истории развития алгебры в современных учебниках Степенная функция
Степенная функция Решение задач
Решение задач Сложение и вычитание десятичных дробей. Урок математики 5 класс Методическая разработка учителя математики Прокопенко Н.В. М
Сложение и вычитание десятичных дробей. Урок математики 5 класс Методическая разработка учителя математики Прокопенко Н.В. М Степень с натуральным показателем
Степень с натуральным показателем Ұқсастық шаралары
Ұқсастық шаралары Понятие логарифмов. Урок алгебры в 10 классе
Понятие логарифмов. Урок алгебры в 10 классе Линейная алгебра. Векторы
Линейная алгебра. Векторы Деление с остатком. Устные упражнения
Деление с остатком. Устные упражнения Цепи. Циклы
Цепи. Циклы Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей