Дискретная математика. Основные понятия теории множеств. (Лекция 1.1)

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ МНОЖЕСТВ

ЛЕКЦИЯ 1

§ 1. МНОЖЕСТВО  
Эта глава, по существу, служит развернутым словарем для

Понятие «множество» относится к исходным понятиям математической теории и не является

Основатель теории множеств
Георг Кантор

«Множество есть многое, мыслимое нами как единое»

множество столов в комнате;
множество всех атомов на Марсе;
множество всех рыб

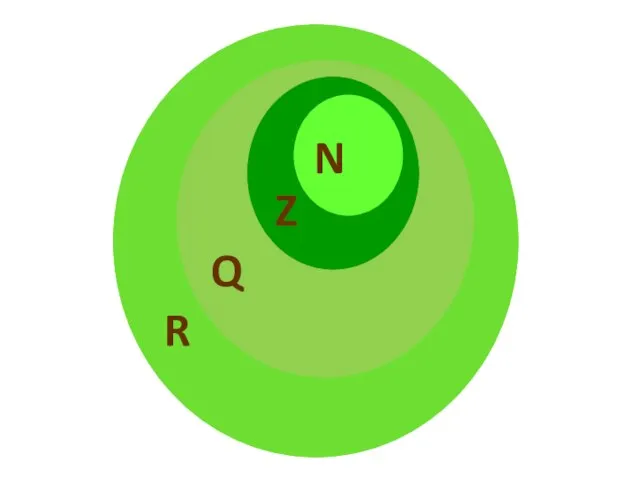
В математике

множество точек (например, окружности),
множество всех решений уравнения sinx=0,5
Для числовых множеств

Объекты, составляющие данное множество, называют его элементами. При этом никаких ограничений

Cпособы задания множеств
полный список (полный перечень) элементов
А = {a1, … ,

Определение 1.1.
Пусть А и В – непустые множества. Если каждый

Определение 1.2.
Пусть А и В – два множества. Множества А

Докажем, что пустое множество единственно.
Действительно, пусть ∅1 и ∅2 – два

Если А ⊆ В и А ≠ В, то А называют

Определение 1.3.
Пусть А – непустое множество. Совокупность всех подмножеств множества

§2. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ

Во всех рассуждениях о нескольких множествах будем предполагать,

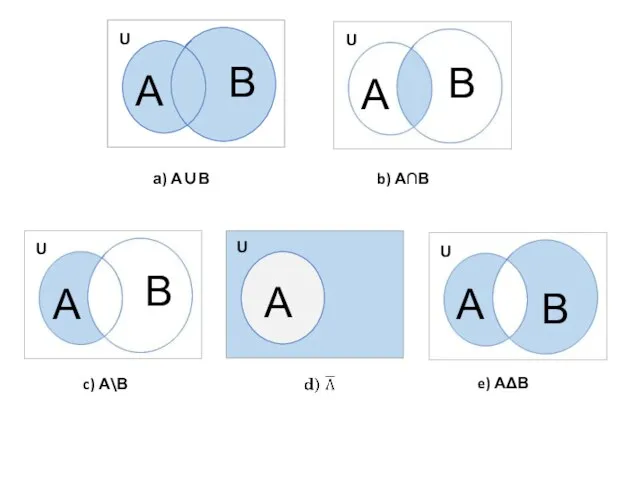
Определение 2.1.
Пересечением множеств А и В называется множество, обозначаемое А∩В

Определение 2.2.
Объединением множеств А и В называется множество, обозначаемое А∪В

Определение 2.3.
Разностью множеств А и В называется множество, обозначаемое А\В

Определение 2.5.
Симметрической разностью множеств А и В называют множество, обозначаемое

Введенные операции объединения, пересечения, разности и симметрической разности являются двуместными. Операция

k

Леонард Эйлер  — швейцарский, немецкий и российский математик, внёсший значительный вклад

а) А∪В

b) А∩В

c) А\В

e) АΔВ

§3. АЛГЕБРА ПОДМНОЖЕСТВ

Пусть Б(Е) - совокупность всех подмножеств множества Е. Б(Е)

Подобно тому, как сложение и умножение чисел удовлетворяют известным законам коммутативности,

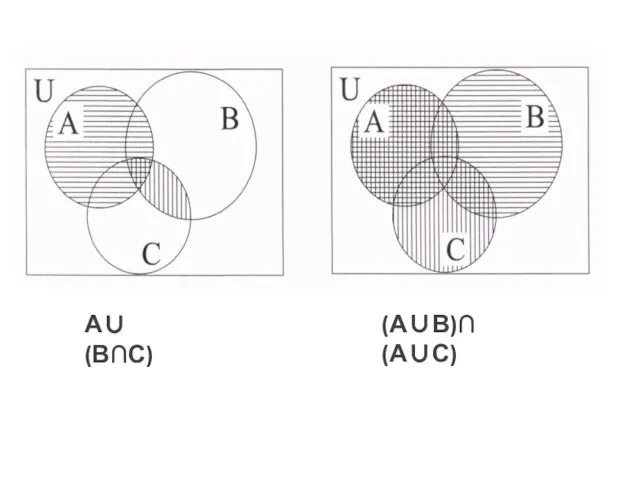
Универсальным методом доказательства вышеприведенных равенств является доказательство, основанное на определении равенств

Доказательство 7а
Пусть x∈A∪(B∩C). Тогда x∈A, или x ∈B∩C. Если x

А∪(В∩С)

(А∪В)∩(А∪С)

§4. Декартово произведение множеств

Декартовым произведением непустых множеств А и В называется

Пусть, например, А = {a1, a2}, В = {b1, b2, b3}.

§5. Бинарные отношения

Определение 5.1.
Бинарным отношением, определенным на паре множеств А

Пусть А = {a1,a2}, B = {b1, b2} . Выпишем все

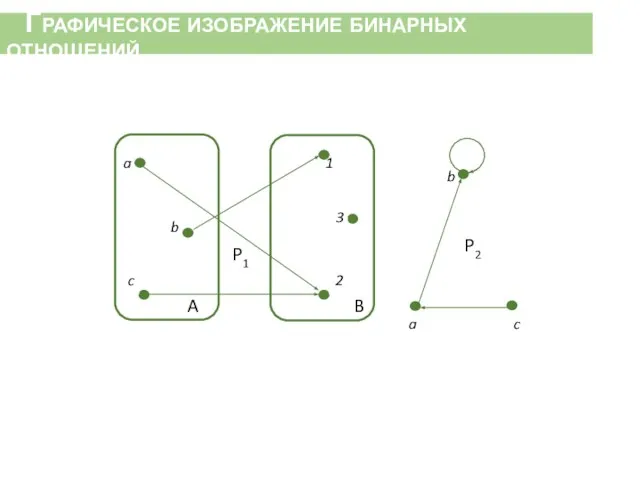
Пусть R — бинарное отношение, определенное на паре множеств А, В.

Область определения бинарного отношения {(2, 1), (2, 4), (3, 3), (3,

Графическое изображение бинарных отношений

§ 6. N - арные отношения

Примеры:
Пусть, например, А= {а,b,с}, В={с,d}, C={1,2}.
Тогда А×В×С = {(а,с,1), (а,d,1),

Пусть A1, …, An — непустые множества. Всякое подмножество R их

Пример
Пусть:
А – множество дней сессии,
В = {8-00,14-00},
С - множество

§ 7. Специальные бинарные отношения

Определение 7.1.
Пусть А – произвольное множество.

Определение 7.3.
Пусть Р – бинарное отношение на множестве А: P