Содержание
- 2. Базовые понятия: множество граф бинарное отношение смежность инцидентность цикл матрица Термины Ключевые слова: матрица смежностей матрица
- 3. Кристофидес Н. Теория графов. Алгоритмический подход. М.: Мир, 1978. С. 25-27. Харари Ф. Теория графов: Пер.
- 4. Основные принципы теории графов используются при построении математической модели для проектирования и анализа сетей ЭВМ Наиболее
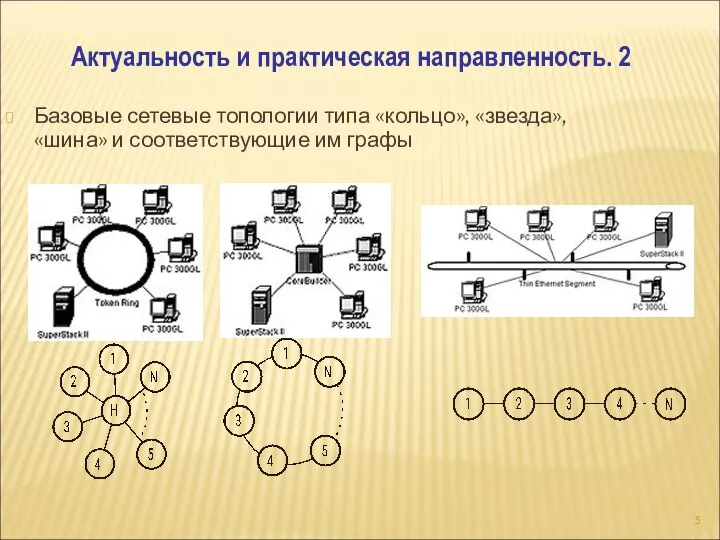
- 5. Базовые сетевые топологии типа «кольцо», «звезда», «шина» и соответствующие им графы Актуальность и практическая направленность. 2
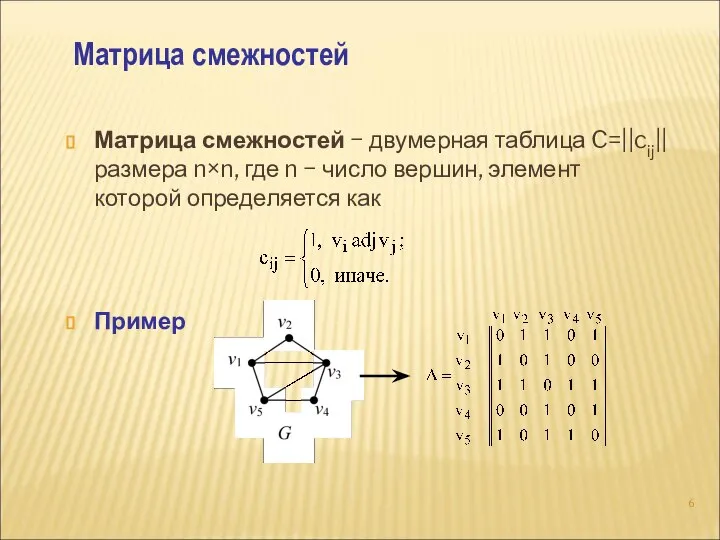
- 6. Матрица смежностей − двумерная таблица C=||cij|| размера n×n, где n − число вершин, элемент которой определяется
- 7. Для неориентированного графа матрица смежностей является симметричной Для ориентированного свойство симметрии не обязательно. Элемент матрицы определяется
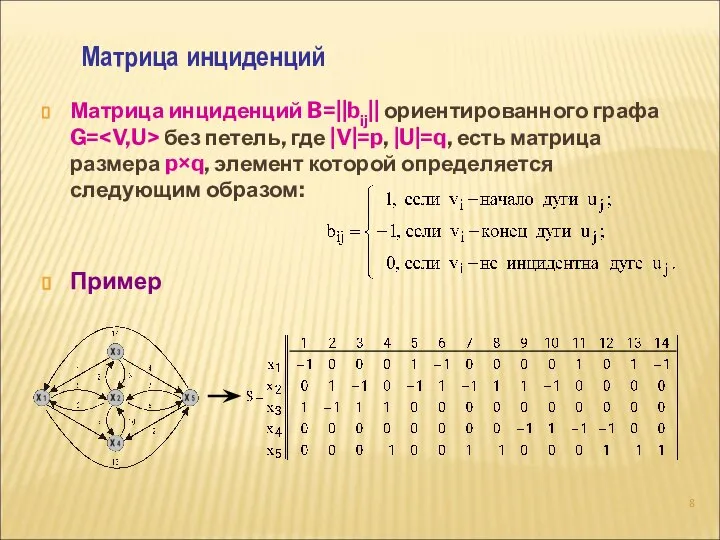
- 8. Матрица инциденций B=||bij|| ориентированного графа G= без петель, где |V|=p, |U|=q, есть матрица размера p×q, элемент
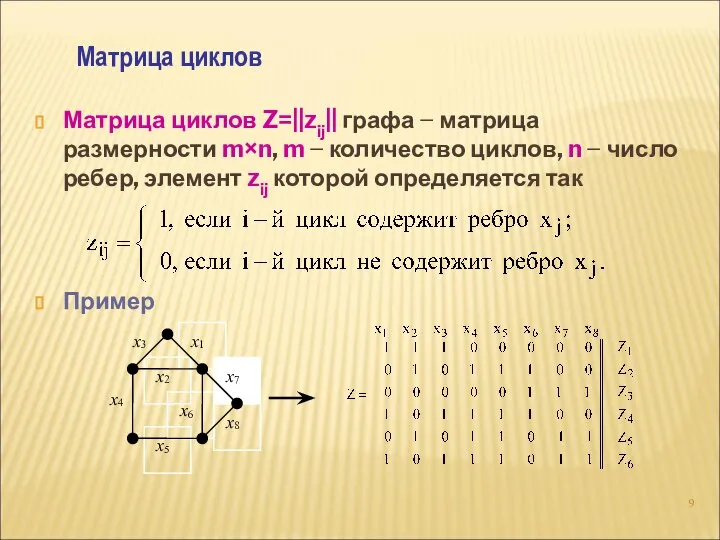
- 9. Матрица циклов Z=||zij|| графа − матрица размерности m×n, m − количество циклов, n − число ребер,
- 10. Пример Неоднозначность представления графа матрицей циклов
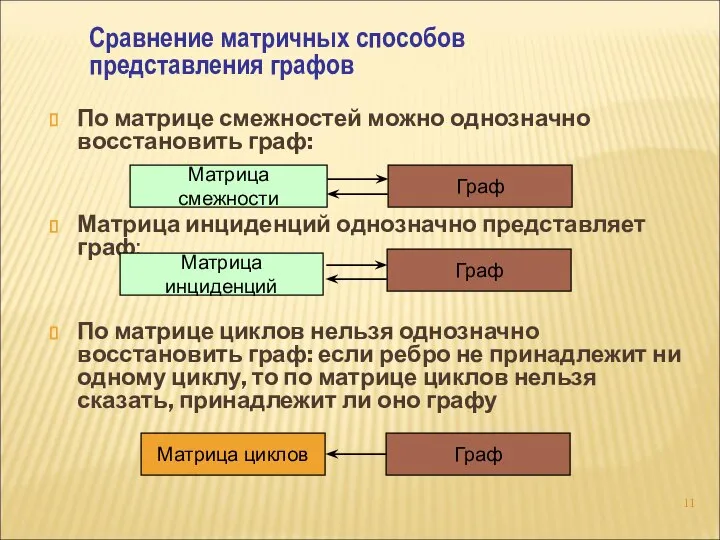
- 11. По матрице смежностей можно однозначно восстановить граф: Матрица инциденций однозначно представляет граф: По матрице циклов нельзя
- 12. Выбор наилучшего представления определяется требованиями конкретной задачи Используются комбинации или модификации известных представлений Способы представления графов
- 13. Time-Out
- 14. Свойства модели: компактность представления информации о графе; привязка к распространенному математическому аппарату; наличие эффективных методов анализа
- 16. Скачать презентацию








 Обыкновенные дроби и их применение
Обыкновенные дроби и их применение Угол между прямыми. Углы с сонаправленными сторонами
Угол между прямыми. Углы с сонаправленными сторонами Открытый урок математики в 5 классе. Подготовила учитель математики ГБОУ СОШ №285 имени В.А. Молодцова Портяная Галина Анатольевн
Открытый урок математики в 5 классе. Подготовила учитель математики ГБОУ СОШ №285 имени В.А. Молодцова Портяная Галина Анатольевн Применение координатно - векторного метода при решении задач
Применение координатно - векторного метода при решении задач 0пределение расстояния до недоступной точки
0пределение расстояния до недоступной точки Теорема Фалеса
Теорема Фалеса Математика. Математические модели
Математика. Математические модели Аттестационная работа. Разработка кружка по математике «Школа юного математика». Развивать логические способности учащихся
Аттестационная работа. Разработка кружка по математике «Школа юного математика». Развивать логические способности учащихся Измерение углов
Измерение углов Финансовая математика в задачах ЕГЭ и практической деятельности человека
Финансовая математика в задачах ЕГЭ и практической деятельности человека Распределение простых чисел
Распределение простых чисел Счастливый случай. Игра
Счастливый случай. Игра Рене́ Дека́рт
Рене́ Дека́рт Решение квадратных уравнений
Решение квадратных уравнений Подготовка к итоговой контрольной работе по математике. 5 класс
Подготовка к итоговой контрольной работе по математике. 5 класс Функция регрессии
Функция регрессии Уравнения следствия
Уравнения следствия Нормальный закон распределения
Нормальный закон распределения 100 В чем измеряется площадь земли? A в килограммах B в арах C в кубических метрах D в минутах
100 В чем измеряется площадь земли? A в килограммах B в арах C в кубических метрах D в минутах  МОУ СОШ № 37 г. Архангельска МОУ СОШ № 37 г. Архангельска Организация работы математического кружка «Эврика» Садовина В. Е.,
МОУ СОШ № 37 г. Архангельска МОУ СОШ № 37 г. Архангельска Организация работы математического кружка «Эврика» Садовина В. Е.,  Презентация по математике "Решение простейших логарифмических неравенств" - скачать бесплатно
Презентация по математике "Решение простейших логарифмических неравенств" - скачать бесплатно Прямоугольный параллелепипед
Прямоугольный параллелепипед Комплексные числа
Комплексные числа Презентация на тему Линии пересекающиеся и непересекающиеся» УМК
Презентация на тему Линии пересекающиеся и непересекающиеся» УМК  Конусның күләме
Конусның күләме Прямая пропорциональность
Прямая пропорциональность Диофантово уравнение
Диофантово уравнение Математики и математика в годы Великой Отечественной войны
Математики и математика в годы Великой Отечественной войны