Содержание
- 2. Межотраслевой баланс Межотраслевой баланс (МОБ, метод «затраты-выпуск») — экономико-математическая балансовая модель, характеризующая межотраслевые производственные взаимосвязи в
- 3. Межотраслевой баланс представлен в виде системы линейных уравнений. Межотраслевой баланс (МОБ) представляет собой таблицу, в которой
- 4. В межотраслевом балансе расположены три квадранта: В первом отражается промежуточное потребление и система производственных связей Во
- 5. Возникновение межотраслевого баланса Теоретические основы межотраслевого баланса были разработаны в СССР в 1923—1924 гг. В 30-е
- 6. Применение балансового метода Балансовый метод применяется для анализа, нормирования, прогноза, планирования производства и распределения продукции на
- 7. Модель межотраслевого баланса В модели межотраслевого баланса предполагается, что народное хозяйство состоит из множества отраслей, каждая
- 8. Сложившаяся в соответствии с потребностями отраслей структура потоков товаров и услуг отражается в математической модели межотраслевого
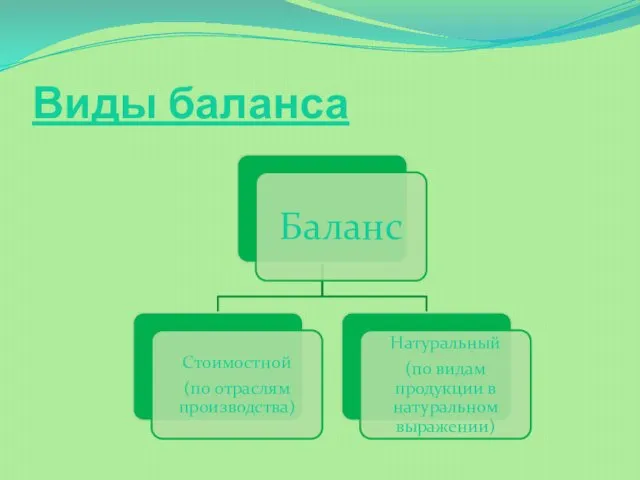
- 9. Виды баланса
- 10. Стоимостной баланс В стоимостном балансе переменные х1, х2, … , хn означают объемы валовой продукции первой,
- 11. Натуральный баланс В натуральном балансе переменные х1, х2, … , хn означают объемы n видов производственных
- 12. В матричной форме системы уравнений (1) межотраслевой стоимостной и межпродуктовый натуральный балансы имеют одинаковое выражение. В
- 13. Однако стоимостной баланс в отличие от натурального наряду с уравнениями xj = в форме распределения продукции
- 14. ……………………………………………………… (3) Это преобразование системы(1) приводит ее к обычной математической форме системы n линейных уравнений с
- 15. Коэффициенты называются коэффициентами прямых затрат. Для всех отраслей их задают в виде матрицы: (4)
- 16. Коэффициенты прямых затрат в натуральном балансе означают технологические нормы расхода продукта i на производство единицы продукта
- 17. В системе уравнений (3) все неизвестные х1, х2, … , хn перенесем в левую часть уравнения
- 18. Модель межотраслевого баланса (5) имеет простую матричную форму записи (Е – А) Х = У и
- 19. В первой задаче планируется валовой выпуск продукции, а конечная продукция является производным показателем. Такой подход легче
- 20. Для того чтобы матрица коэффициентов прямых материальных затрат А была продуктивной, необходимо и достаточно, чтобы выполнялось
- 22. Скачать презентацию


















 Решение транспортной задачи. Составление опорного плана
Решение транспортной задачи. Составление опорного плана Определение параллельных прямых
Определение параллельных прямых Диаграммы. Круговые диаграммы
Диаграммы. Круговые диаграммы Неравенства с двумя переменными и их системы
Неравенства с двумя переменными и их системы Деление десятичных дробей на натуральное число
Деление десятичных дробей на натуральное число Логарифмические уравнения
Логарифмические уравнения Практические приложения подобия треугольников. О подобии произвольных фигур
Практические приложения подобия треугольников. О подобии произвольных фигур Задачи о дачном участке
Задачи о дачном участке Решение уравнений. Повторение
Решение уравнений. Повторение Золотое сечение божественная мера красоты
Золотое сечение божественная мера красоты Биквадратные уравнения
Биквадратные уравнения Маршруты. Расстояния
Маршруты. Расстояния Тригонометрические формулы
Тригонометрические формулы Методика изучения массы
Методика изучения массы Квадратные уравнения
Квадратные уравнения Тренажёр. Таблица умножения. «Юные водители»
Тренажёр. Таблица умножения. «Юные водители» Аттестационная работа. Исследовательская деятельность учащихся на уроках математики
Аттестационная работа. Исследовательская деятельность учащихся на уроках математики Нахождение процента от величины (часть 2)
Нахождение процента от величины (часть 2) Моделирование в условиях риска и неопределенности
Моделирование в условиях риска и неопределенности Основные законы распределения случайных величин
Основные законы распределения случайных величин Кроссворд по теме многогранники
Кроссворд по теме многогранники Аукцион «Продажа имения старой графини» ( математическая игра для 10-11 классов) Составила учитель математики Давлятова Л.Н. П. Че
Аукцион «Продажа имения старой графини» ( математическая игра для 10-11 классов) Составила учитель математики Давлятова Л.Н. П. Че Деление. Порядок выполнения действий. Степень числа. Квадрат и куб числа. Формулы. Площадь. Формулы площади. (5 класс)
Деление. Порядок выполнения действий. Степень числа. Квадрат и куб числа. Формулы. Площадь. Формулы площади. (5 класс) Презентация на тему Многогранники
Презентация на тему Многогранники  Решение уравнений графическим способом
Решение уравнений графическим способом Оценка достоверности статистических параметров. Статистический анализ вариации количественных признаков
Оценка достоверности статистических параметров. Статистический анализ вариации количественных признаков Первый признак подобия треугольников, применение его при решении задач
Первый признак подобия треугольников, применение его при решении задач Число и цифра 7
Число и цифра 7