Содержание
- 2. Окружающие нас предметы обладают разнообразными свойствами, которые изучаются различными науками
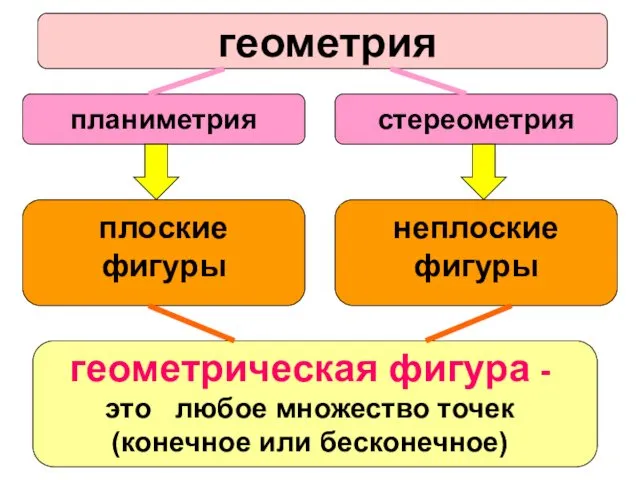
- 3. «Геометрия» с греч. γεωμετρια -«землемерие» («γεω »– земля, «μετρια » – измеряю) Геометрия возникла в Древнем
- 4. Основные достижения в области математики были систематизированы в 3 в. до н.э. греческим ученым Евклидом и
- 6. Фигура – латинское слово, означающее образ, вид, начертание. Этот термин вошел в общее употребление, начиная с
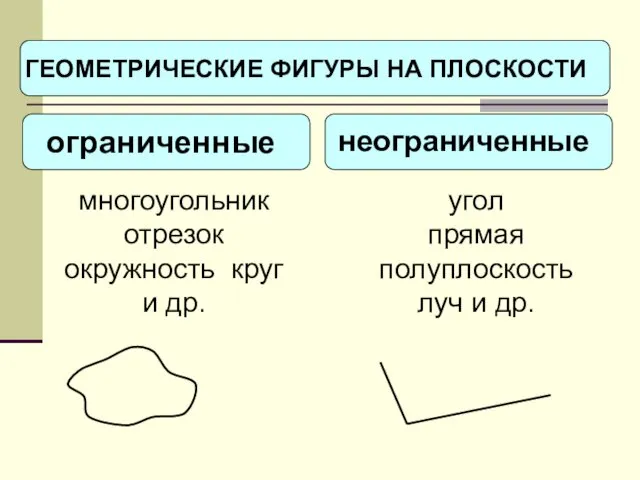
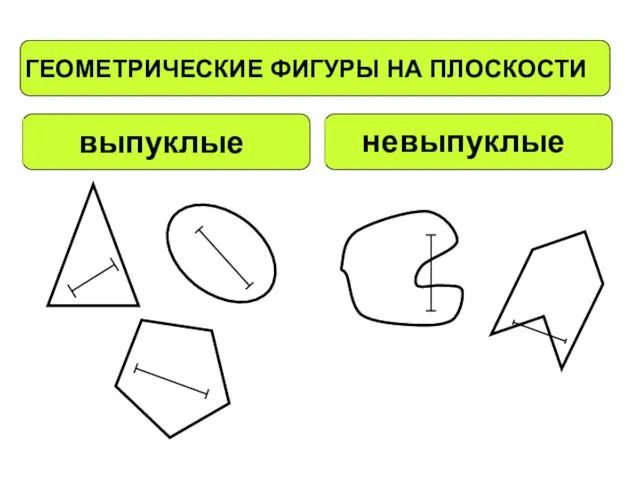
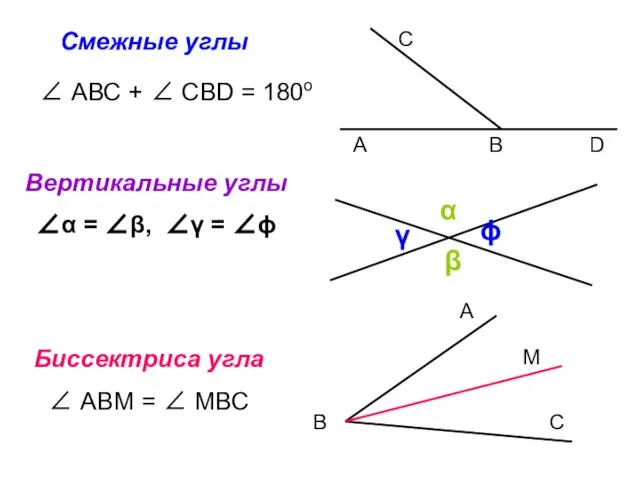
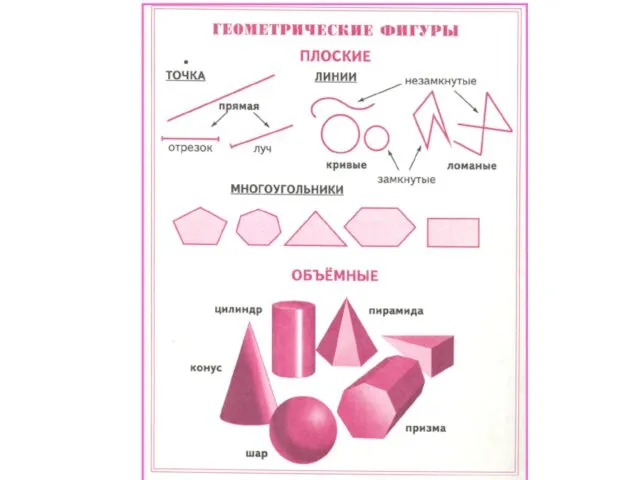
- 7. многоугольник отрезок окружность круг и др. угол прямая полуплоскостьлуч и др.
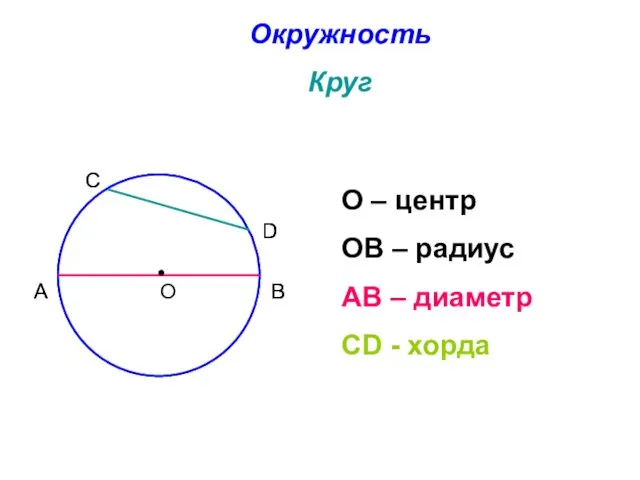
- 11. Окружность Круг О – центр ОВ – радиус АВ – диаметр СD - хорда
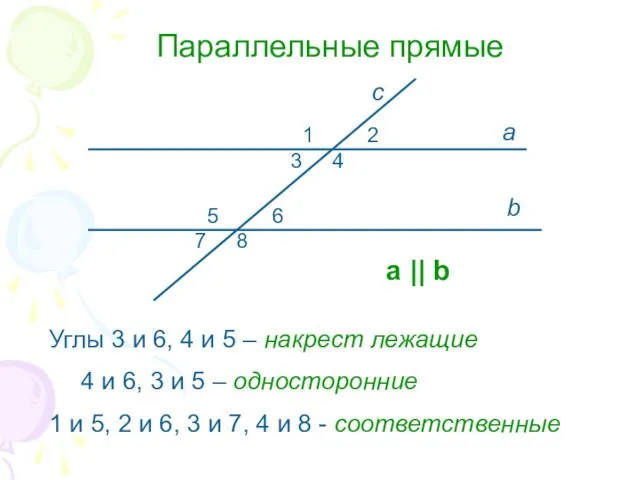
- 12. Параллельные прямые Углы 3 и 6, 4 и 5 – накрест лежащие 4 и 6, 3
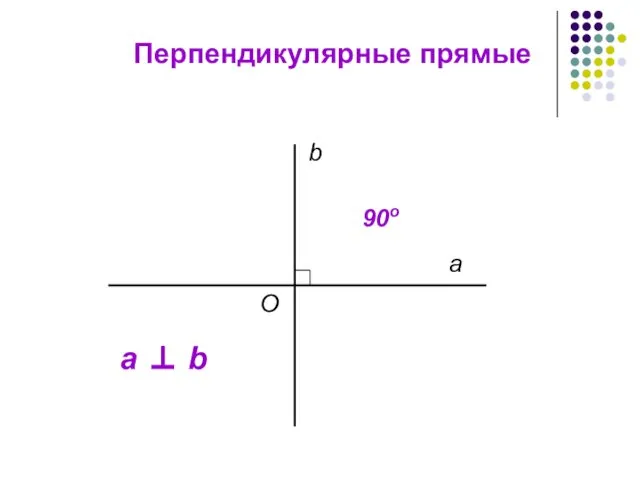
- 13. Перпендикулярные прямые а b О 90о а ⊥ b
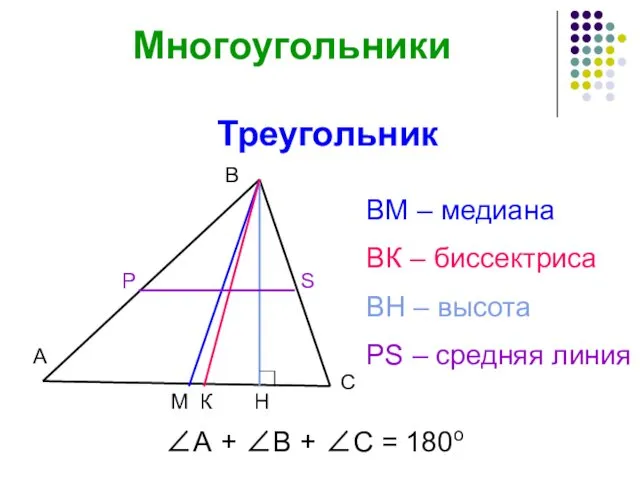
- 14. Треугольник ВМ – медиана ВК – биссектриса ВН – высота РS – средняя линия ∠А +
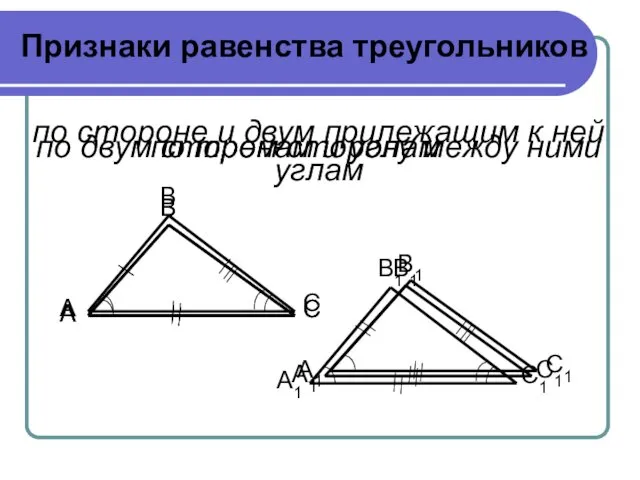
- 17. Признаки равенства треугольников
- 18. Признаки равенства прямоугольных треугольников - по гипотенузе и острому углу; - по гипотенузе и катету; -
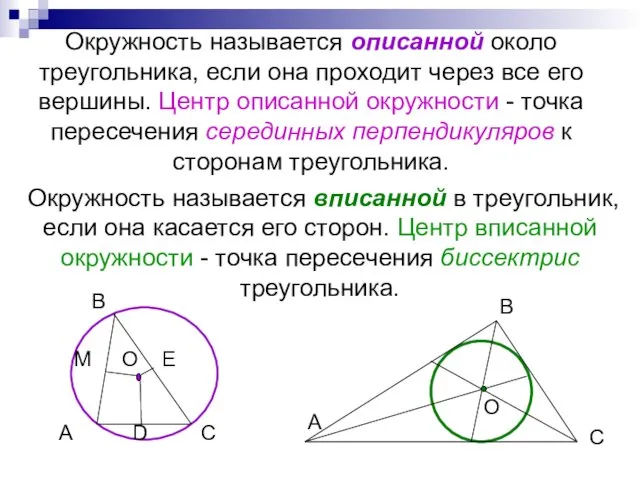
- 19. Окружность называется описанной около треугольника, если она проходит через все его вершины. Центр описанной окружности -
- 20. Ромбы без прямых углов
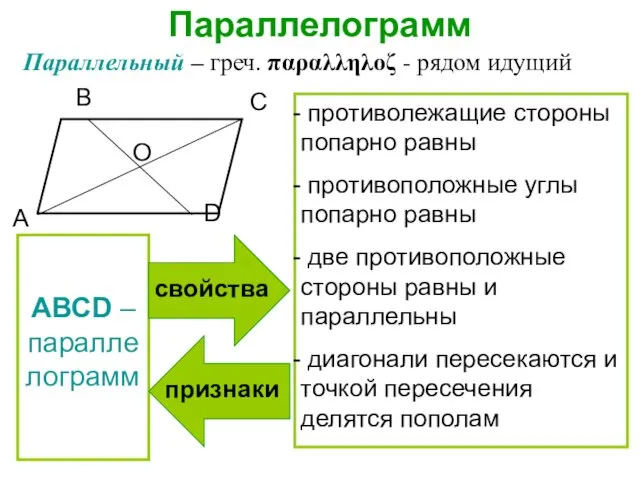
- 21. Параллелограмм Параллельный – греч. παραλληλοζ - рядом идущий АВСD – параллелограмм противолежащие стороны попарно равны противоположные
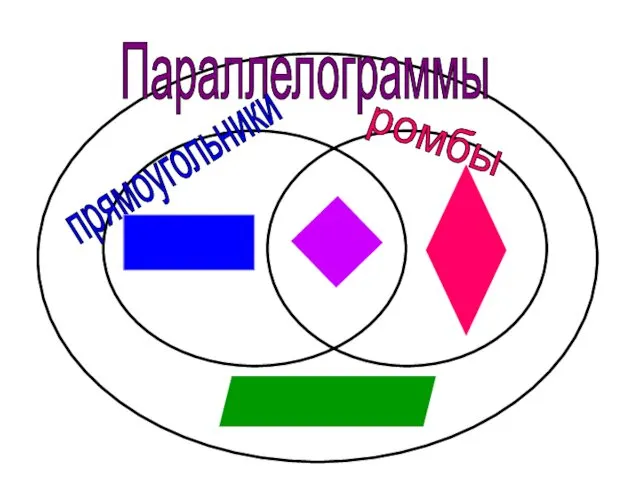
- 22. Параллелограммы прямоугольники ромбы
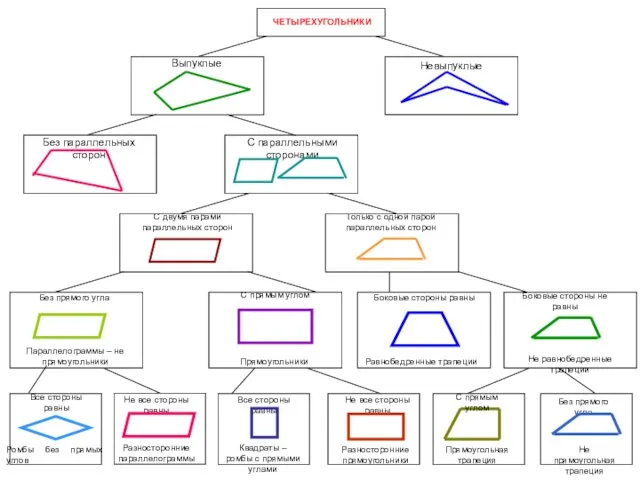
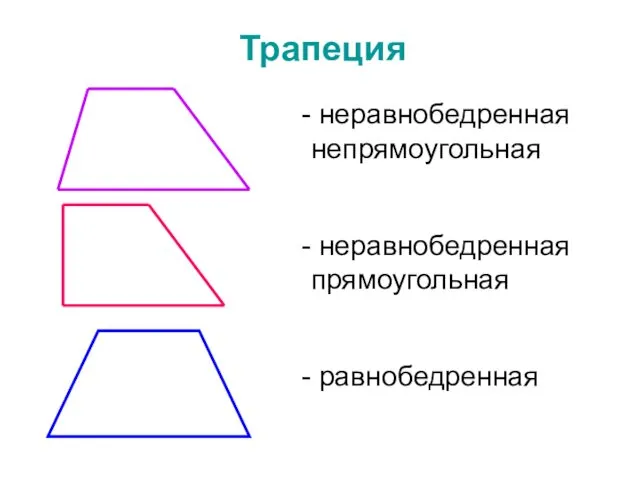
- 23. Трапеция неравнобедренная непрямоугольная неравнобедренная прямоугольная равнобедренная
- 25. Пространственные геометрические фигуры многогранники тела вращения
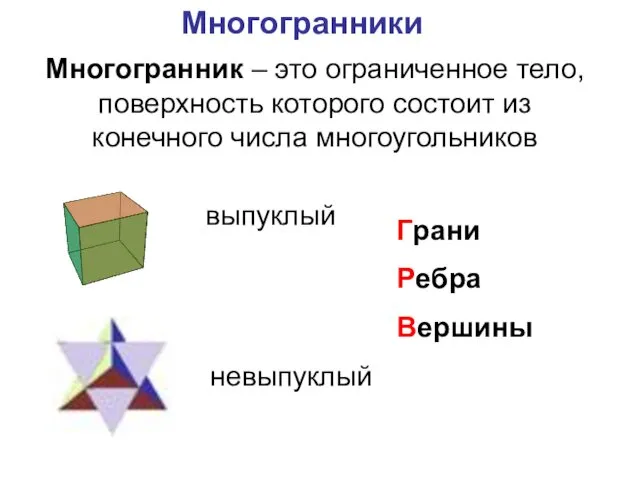
- 26. Многогранники Многогранник – это ограниченное тело, поверхность которого состоит из конечного числа многоугольников выпуклый невыпуклый Грани
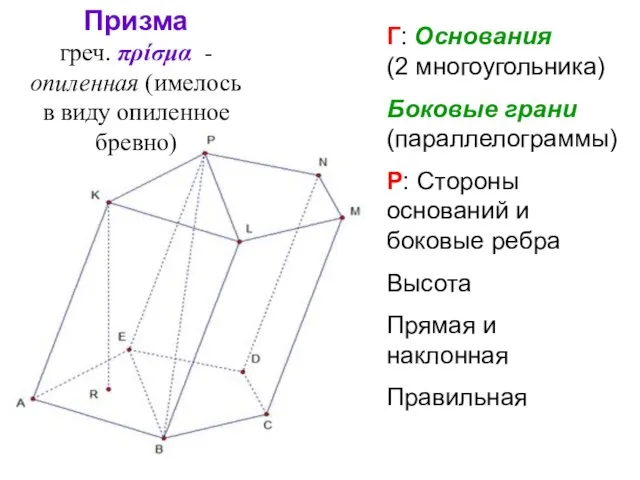
- 27. Призма греч. πρίσμα - опиленная (имелось в виду опиленное бревно) Г: Основания (2 многоугольника) Боковые грани
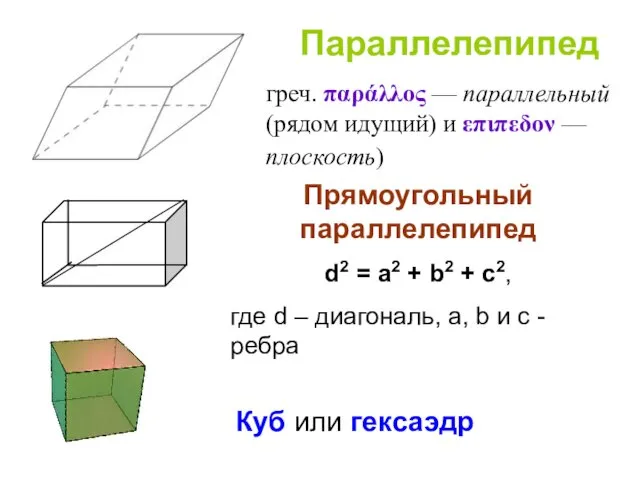
- 28. Параллелепипед греч. παράλλος — параллельный (рядом идущий) и επιπεδον — плоскость) Куб или гексаэдр Прямоугольный параллелепипед
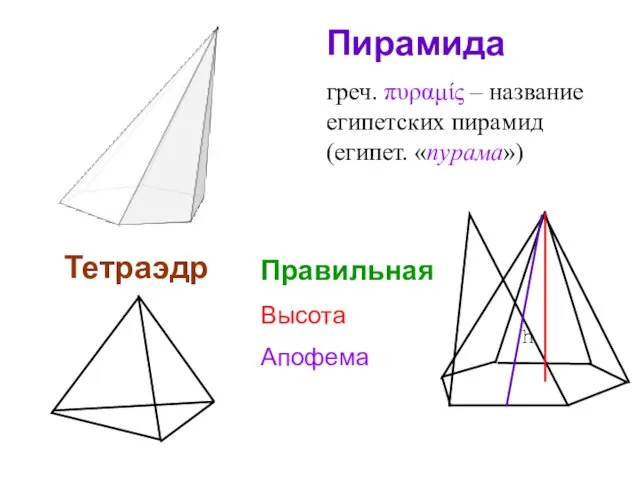
- 29. Пирамида греч. πυραμίς – название египетских пирамид (египет. «пурама») Тетраэдр Правильная Высота Апофема
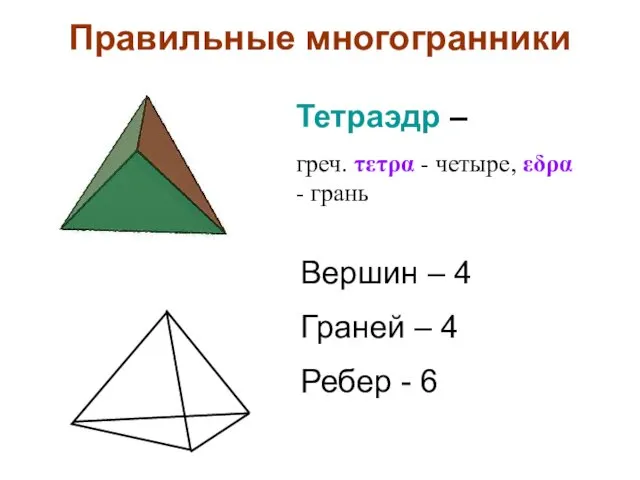
- 30. Правильные многогранники Вершин – 4 Граней – 4 Ребер - 6 Тетраэдр – греч. τετρα -
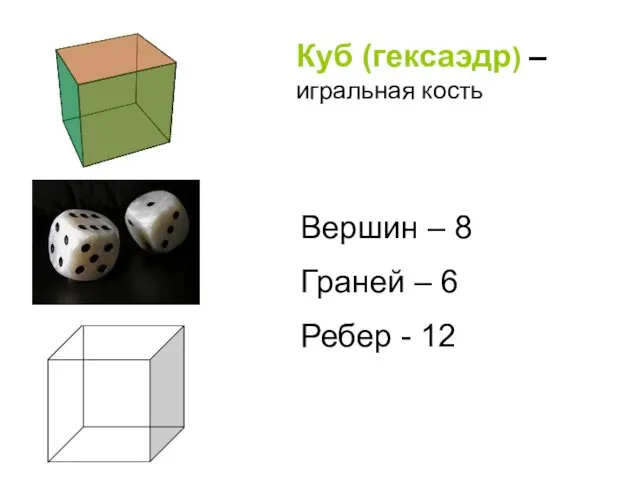
- 31. Куб (гексаэдр) – игральная кость Вершин – 8 Граней – 6 Ребер - 12
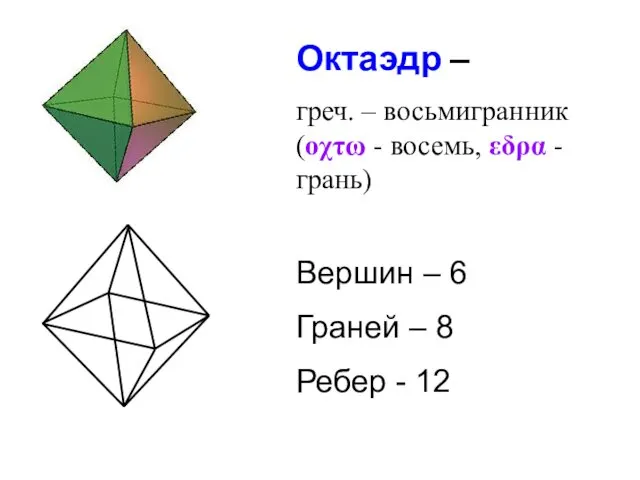
- 32. Октаэдр – греч. – восьмигранник (οχτω - восемь, εδρα - грань) Вершин – 6 Граней –
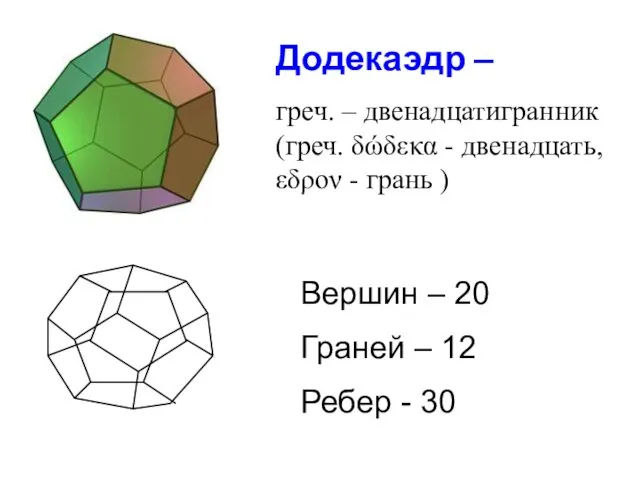
- 33. Додекаэдр – греч. – двенадцатигранник (греч. δώδεκα - двенадцать, εδρον - грань ) Вершин – 20
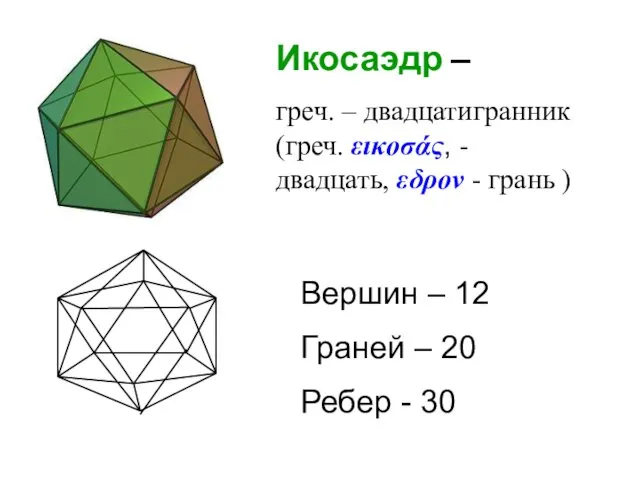
- 34. Икосаэдр – греч. – двадцатигранник (греч. εικοσάς, - двадцать, εδρον - грань ) Вершин – 12
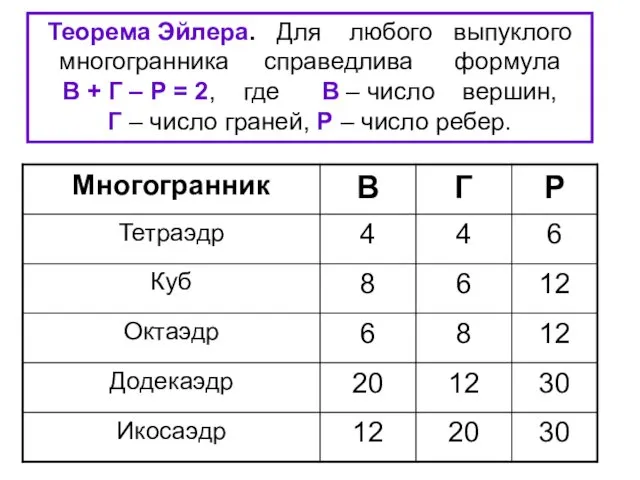
- 35. Теорема Эйлера. Для любого выпуклого многогранника справедлива формула В + Г – Р = 2, где
- 36. Звездчатые многогранники
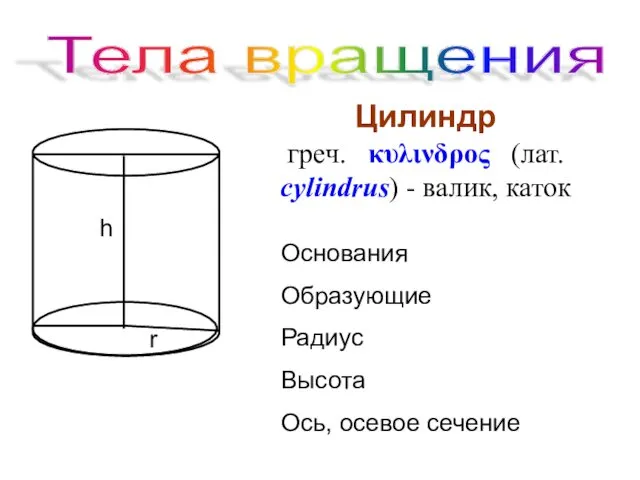
- 37. Тела вращения Цилиндр греч. κυλινδρος (лат. cylindrus) - валик, каток Основания Образующие Радиус Высота Ось, осевое
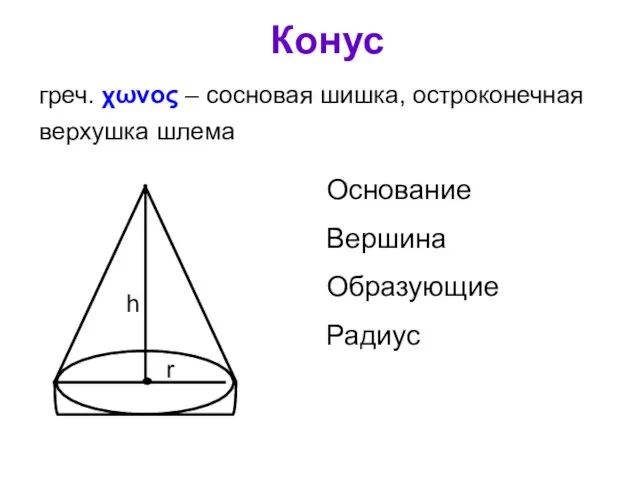
- 38. Конус греч. χωνος – сосновая шишка, остроконечная верхушка шлема Основание Вершина Образующие Радиус
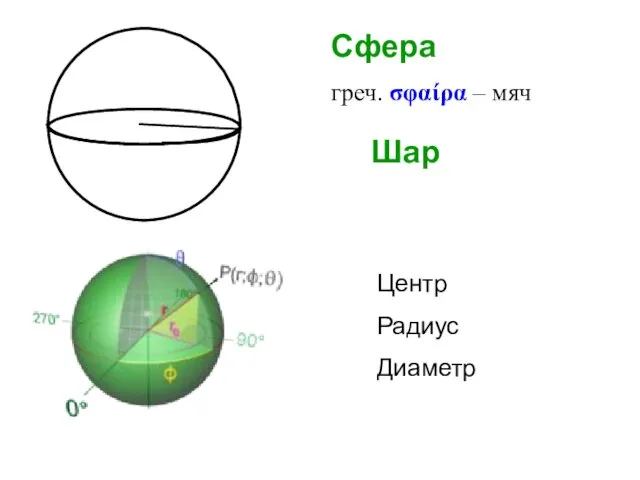
- 39. Сфера греч. σφαίρα – мяч Центр Радиус Диаметр Шар
- 40. ПРЕОБРАЗОВАНИЯ ГЕОМЕТРИЧЕСКИХ ФИГУР Понятие геометрического преобразования Пусть задана некоторая фигура F и каждой точке фигуры F
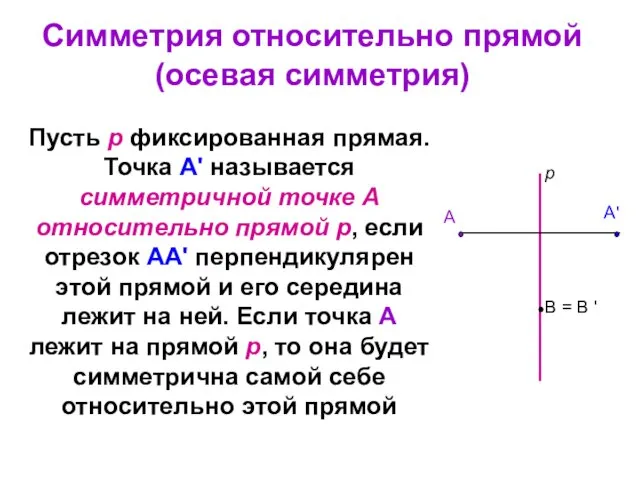
- 41. Пусть р фиксированная прямая. Точка А' называется симметричной точке А относительно прямой р, если отрезок АА'
- 42. Пусть F – данная фигура, р – фиксированная прямая. Преобразование фигуры F в фигуру F', при
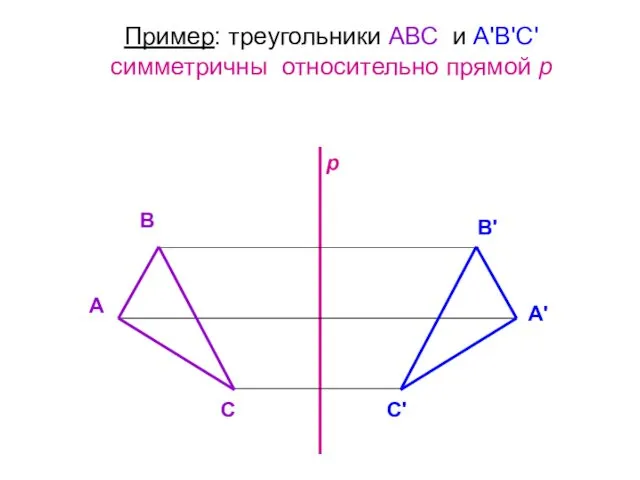
- 43. Пример: треугольники АВС и А'В'С' симметричны относительно прямой р
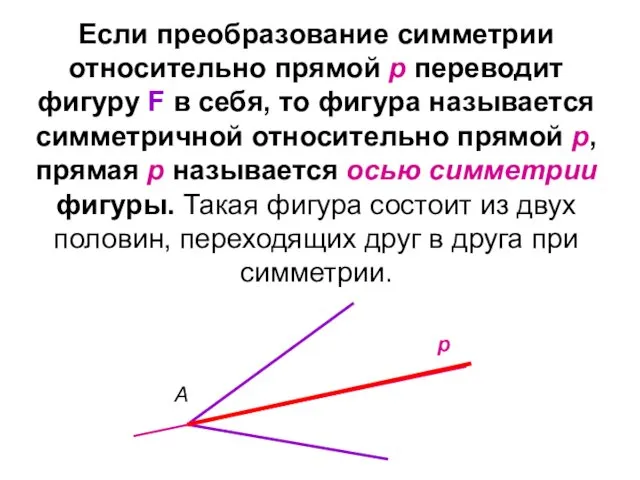
- 44. Если преобразование симметрии относительно прямой р переводит фигуру F в себя, то фигура называется симметричной относительно
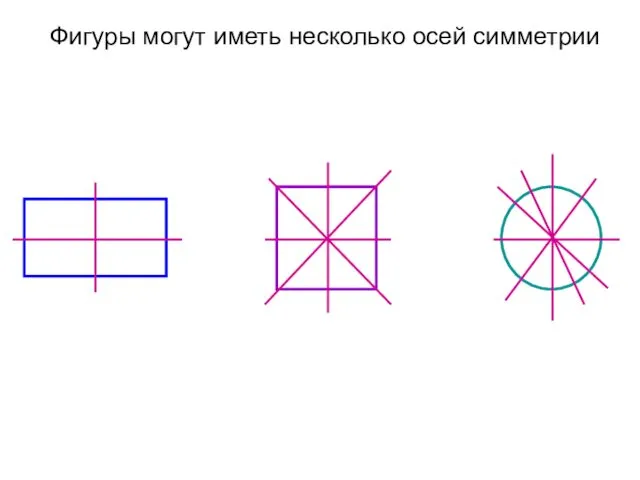
- 45. Фигуры могут иметь несколько осей симметрии
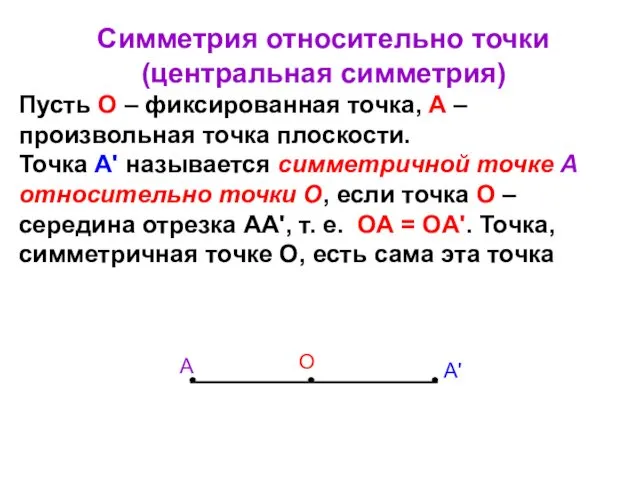
- 46. Симметрия относительно точки (центральная симметрия) Пусть О – фиксированная точка, А – произвольная точка плоскости. Точка
- 47. Пусть F – данная фигура и О – фиксированная точка плоскости. Преобразование фигуры F в фигуру
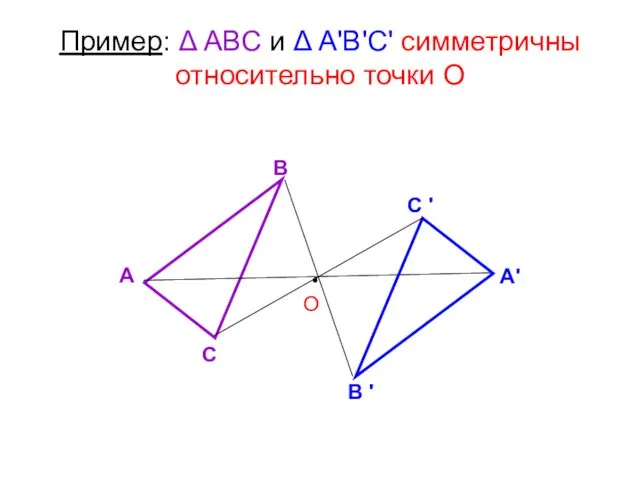
- 48. Пример: Δ АВС и Δ А'В'С' симметричны относительно точки О
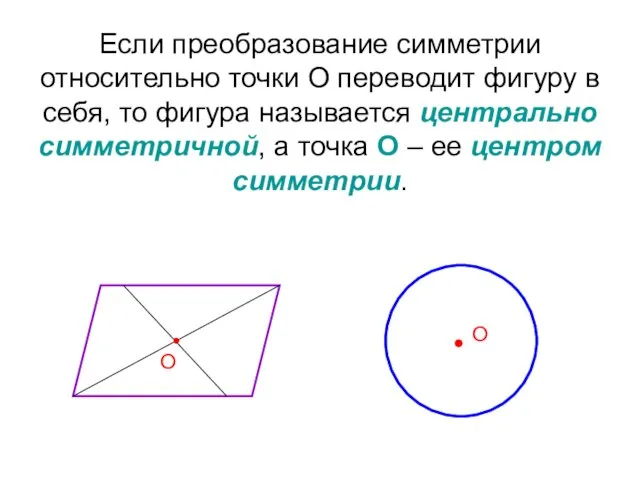
- 49. Если преобразование симметрии относительно точки О переводит фигуру в себя, то фигура называется центрально симметричной, а
- 51. Скачать презентацию










 Скалярное произведение векторов
Скалярное произведение векторов Вариация. Вариация көрсеткіштері туралы түсінік және оның міндеттері, түрлері
Вариация. Вариация көрсеткіштері туралы түсінік және оның міндеттері, түрлері Параллелепипеды. Прямоугольные параллелепипеды. Куб
Параллелепипеды. Прямоугольные параллелепипеды. Куб Полиномы от одной переменной. Нохождение НОД. (Лекция 5.2)
Полиномы от одной переменной. Нохождение НОД. (Лекция 5.2) Конспект урока математики. 4класс.
Конспект урока математики. 4класс.  Решение квадратных уравнений. Урок обобщения и систематизации знаний
Решение квадратных уравнений. Урок обобщения и систематизации знаний Уравнения фигур. 9 класс
Уравнения фигур. 9 класс Множеества и операции над ними
Множеества и операции над ними Basic dynamic elements
Basic dynamic elements Логарифмы в природе
Логарифмы в природе Сумма и разность десятичных дробей
Сумма и разность десятичных дробей Открытый урок по математике в 6 классе
Открытый урок по математике в 6 классе Симметричный мир
Симметричный мир Минимизация стоимости выполнения работ при ограничении на время их выполнения
Минимизация стоимости выполнения работ при ограничении на время их выполнения Площадь четырёхугольника 9 класс Карпова Татьяна Андреевна
Площадь четырёхугольника 9 класс Карпова Татьяна Андреевна Матриці та дії над ними
Матриці та дії над ними Уравнения и методы их решения
Уравнения и методы их решения 5 КЛАСС ОБОБЩАЮЩИЙ УРОК ПО ТЕМЕ «НАТУРАЛЬНЫЕ ЧИСЛА»
5 КЛАСС ОБОБЩАЮЩИЙ УРОК ПО ТЕМЕ «НАТУРАЛЬНЫЕ ЧИСЛА»  Խնդիր Հաշվել a, b, c կողմեր ունեցող եռանկյան մակերեսը
Խնդիր Հաշվել a, b, c կողմեր ունեցող եռանկյան մակերեսը Деление дробей
Деление дробей Центрально - симметричные фигуры
Центрально - симметричные фигуры Теоремы ТЗ
Теоремы ТЗ Векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия, равенство векторов
Векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия, равенство векторов Аттестационная работа. Исследовательская деятельность учащихся при построении доказательств по математике. (5-6 класс)
Аттестационная работа. Исследовательская деятельность учащихся при построении доказательств по математике. (5-6 класс) Статистические исследования
Статистические исследования Матрицы
Матрицы Многогранники. Правильные многогранники
Многогранники. Правильные многогранники Занимательные задачи по математике Выполнили: Баринова Катя Крылова Света Галкина Лера 7А класс
Занимательные задачи по математике Выполнили: Баринова Катя Крылова Света Галкина Лера 7А класс