Содержание
- 2. Учебные цели: 1. Рассмотреть важнейшие понятия векторный алгебры. 2. Раскрыть смысл линейных операций над векторами и
- 3. Учебные вопросы: Векторы: основные понятия и виды. 2. Действия с векторами. 3. Скалярное, векторное и смешанное
- 4. Величины, которые полностью определяются своими численными значениями, называются скалярными. Например, площадь, объем, температура, работа, масса. Другие
- 5. Отрезок называется направленным, если считается, что у него есть начало и конец. Вектор – это направленный
- 6. ПЕРВЫЙ УЧЕБНЫЙ ВОПРОС ВЕКТОРЫ: ОСНОВНЫЕ ПОНЯТИЯ И ВИДЫ
- 7. Длиной (модулем) вектора называется длина отрезка AB, то есть расстояние между началом и концом вектора. Обозначение:
- 8. Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор считается коллинеарным любому вектору. Два вектора
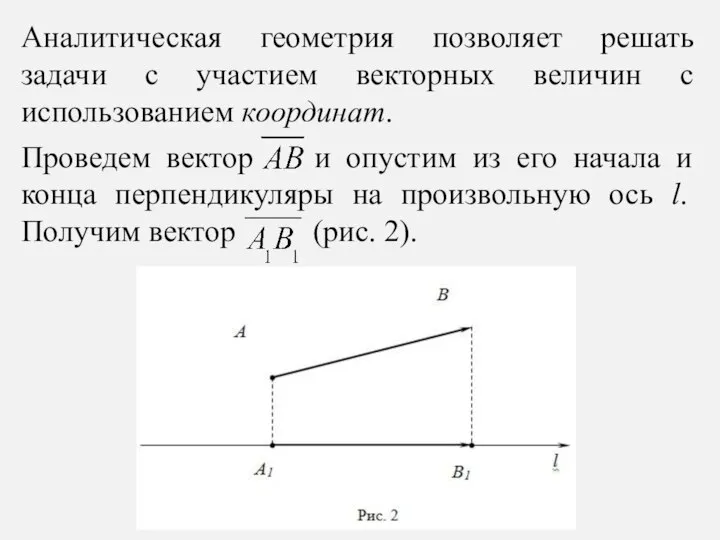
- 9. Аналитическая геометрия позволяет решать задачи с участием векторных величин с использованием координат. Проведем вектор и опустим
- 10. Проекцией вектора на ось называется положительное число , если вектор и ось одинаково направлены, и отрицательное
- 11. Обозначение координат вектора: Или: Обратите внимание: координаты вектора, в отличие от координат точки, заключаются в фигурные
- 12. Теорема 1. Каковы бы ни были две точки и , координаты вектора определяются единственным образом: (По
- 13. Декартова прямоугольная система координат X Y Z О x,y.z - декартовы прямоугольные координаты вектора относительно данной
- 14. Рассмотрим произвольный вектор длина вектора равна: Перенесем его параллельно, совместив начало с началом координат. На основании
- 15. Пусть – орты осей координат, то есть векторы единичной длины, совпадающие по направлению соответственно с координатными
- 16. Теорема 2. Любой трехмерный вектор может быть единственным образом разложен по базису , т.е. представлен в
- 17. Проекция вектора на ненулевой вектор : проекция на любую ось, одинаково направленную с Пусть дана прямая,
- 18. ВТОРОЙ УЧЕБНЫЙ ВОПРОС ДЕЙСТВИЯ С ВЕКТОРАМИ
- 19. Если векторы заданы своими координатами: то линейные операции над векторами сводятся к линейным операциям над координатами
- 20. (координаты разности двух векторов равны разностям соответствующих координат этих векторов); 3. (координаты произведения числа k на
- 21. Используя определение произведения числа на вектор, нетрудно получить условие коллинеарности векторов: векторы и коллинеарны в том
- 22. ТРЕТИЙ УЧЕБНЫЙ ВОПРОС СКАЛЯРНОЕ, ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 23. Вопрос 3. Скалярное, векторное и смешанное произведения векторов Умножение векторов производится по специфическим правилам, и кроме
- 24. 3.1. Скалярное произведение векторов Скалярным произведением двух ненулевых векторов и называется число (скаляр), равное произведению длин
- 25. Основные свойства скалярного произведения Коммутативность (переместительный закон): Ассоциативность (сочетательный закон – по отношению к скалярному множителю):
- 26. 4. Скалярный квадрат вектора равен квадрату его длины: То есть, если вектор возвести скалярно в квадрат,
- 27. Физический смысл скалярного произведения: работа постоянной силы (вектора ), точка приложения которой перемещается из начала в
- 28. Скалярное произведение векторов, заданных координатами Пусть тогда: Доказательство: перемножим скалярно векторы и , разложив их по
- 29. Замечание. Угол между векторами и определяется равенством: Пример 1. Найти скалярное произведение векторов Решение. По формуле
- 30. 3.2. Векторное произведение векторов Три вектора в пространстве называются компланарными, если они лежат в одной плоскости
- 31. Векторным произведением вектора на вектор называется вектор который определяется тремя условиями: 1. Длина вектора равна площади
- 32. 2. Вектор перпендикулярен каждому из векторов и . 3. Векторы , и образуют правую упорядоченную тройку.
- 33. 3. Дистрибутивность: 4. Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулевому вектору их
- 34. 3.3. Смешанное произведение векторов Смешанным произведением трех векторов: , и называется число, равное произведению: Основные свойства
- 35. Замечание. В соответствии со свойством 2 и свойством коммутативности скалярного произведения (свойство 1)), (перемена знаков векторного
- 36. 4. Необходимым и достаточным условием компланарности трех ненулевых векторов является равенство нулю их смешанного произведения (взятого
- 37. Смешанное произведение векторов, заданных координатами Пусть тогда: Пусть
- 38. Пример 3. Найти смешанное произведение векторов: Решение. По формуле (5) находим: Пусть
- 40. Скачать презентацию
















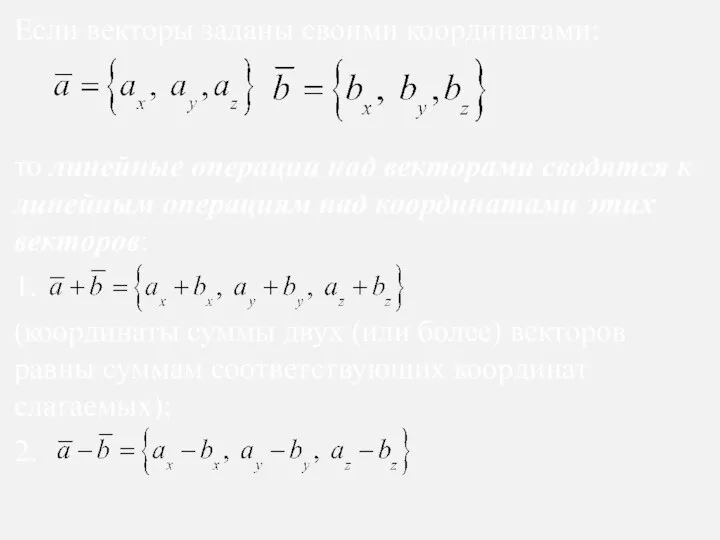



















 Анализ геометрических тел
Анализ геометрических тел Презентация на тему Волшебный квадрат
Презентация на тему Волшебный квадрат Построение отрезка данной длины
Построение отрезка данной длины Задачи с практическим содержанием по теме: «Арифметическая и геометрическая прогрессии»
Задачи с практическим содержанием по теме: «Арифметическая и геометрическая прогрессии» Функции. Игра «Счастливый случай»
Функции. Игра «Счастливый случай» Независимые, зависимые и контролируемые переменные
Независимые, зависимые и контролируемые переменные Геометрия. Повторение программы. 7 – 9 класс
Геометрия. Повторение программы. 7 – 9 класс Гамильтоновы цепи в некоторых типах линейно-выпуклых графов
Гамильтоновы цепи в некоторых типах линейно-выпуклых графов Задачи на движение
Задачи на движение Зеркальная симметрия и параллельный перенос
Зеркальная симметрия и параллельный перенос Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Функция, её свойства и график
Функция, её свойства и график Тест по теме: "Перпендикулярность в пространстве". Практическая часть
Тест по теме: "Перпендикулярность в пространстве". Практическая часть Я вырасту здоровым. Занимательная математика. Вторая младшая группа
Я вырасту здоровым. Занимательная математика. Вторая младшая группа Особливості підготовки до ЗНО 2016 з математики
Особливості підготовки до ЗНО 2016 з математики Логарифмическая функция, её свойства и график
Логарифмическая функция, её свойства и график Урок математики 6 класс Фролова С. Г., учитель математики МКОУ «Лицей» , г. Калачинск, Омской области
Урок математики 6 класс Фролова С. Г., учитель математики МКОУ «Лицей» , г. Калачинск, Омской области Незнайка на планете Математика
Незнайка на планете Математика Решение систем уравнений с двумя переменными
Решение систем уравнений с двумя переменными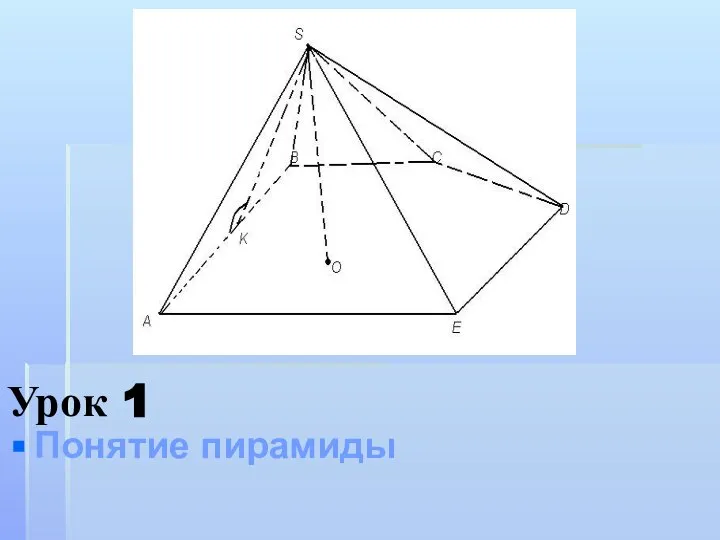 Многогранник пирамида
Многогранник пирамида Теорема косинусов
Теорема косинусов Обобщающий урок по теме «Площадь многоугольника. Теорема Пифагора»
Обобщающий урок по теме «Площадь многоугольника. Теорема Пифагора» Уравнения, 5 класс.
Уравнения, 5 класс.  Пропорциональные отрезки в прямоугольном треугольнике. Признаки подобия треугольников
Пропорциональные отрезки в прямоугольном треугольнике. Признаки подобия треугольников Координаты вектора. Простейшие задачи в координатах
Координаты вектора. Простейшие задачи в координатах Всероссийские проверочные работы
Всероссийские проверочные работы Задачи на движение
Задачи на движение Тренажер. Умножение и деление десятичных дробей
Тренажер. Умножение и деление десятичных дробей