Содержание
- 2. ФИГУРНЫЕ ЧИСЛА. Федоров Даниил МБУЗ СОШ 24 Научный руководитель: Андрейчикова Светлана Владимировна учитель математики
- 3. ПРОБЛЕМНЫЙ ВОПРОС: Какие числа называются фигурными, на какие виды эти числа делятся, применение и история возникновения
- 4. Мотивы выбора темы. Ещё вначале VI века до н.э. греческие математики обнаружили интересный способ рассмотрения чисел,
- 5. ГИПОТЕЗА. В наше время фигурные числа не потеряли свою актуальность, они могут оказать помощь ученику в
- 6. ИСТОРИЯ ВОЗНИКНОВЕНИЯ В строительстве сооружений древности — пирамид, дворцов и храмов — применялись плиты и кирпичи,
- 7. Со времён пифагорейцев традиционно различают следующие виды фигурных чисел Линейные числа — числа, не разлагающиеся на
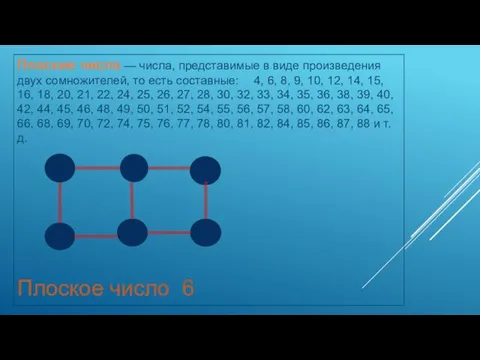
- 8. Плоские числа — числа, представимые в виде произведения двух сомножителей, то есть составные: 4, 6, 8,
- 9. Телесные числа — числа, представимые произведением трёх сомножителей: 8, 12, 16, 18, 20, 24, 27, 28,
- 10. МНОГОУГОЛЬНЫЕ ЧИСЛА —числа, связанные определенным образом с плоским многоугольником. Простейшими из многоуголных чисел являются треугольные числа
- 11. Квадратные числа представляют собой произведение двух одинаковых натуральных чисел, то есть являются полными квадратами: 1, 4,
- 12. Пятиугольные числа 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287,
- 13. Фигурные числа в математике. На мой взгляд, с помощью плоских фигурных чисел легко проиллюстрировать законы умножения.
- 14. Наконец, если "камешки", образующие фигурные числа, мыслить в виде равных по площади квадратиков, то, укладывая их
- 16. Скачать презентацию












 Исследовательская работа. Тема:Уравнения и неравенства, содержащие знак модуля
Исследовательская работа. Тема:Уравнения и неравенства, содержащие знак модуля Тест по теме: Комбинация фигур
Тест по теме: Комбинация фигур Числовые функции, свойства функции, 10 класс
Числовые функции, свойства функции, 10 класс Произведение многочленов
Произведение многочленов Множество. Элемент множества.
Множество. Элемент множества.  Зеркальная симметрия
Зеркальная симметрия  Четырехугольники
Четырехугольники Сопряжение. Геометрические построения
Сопряжение. Геометрические построения Тест по теме: "Координаты точки и координаты вектора"
Тест по теме: "Координаты точки и координаты вектора" Муниципальное образовательное учреждение «Гимназия №20» секция теоретической математики Автор: Буравлев Степан, 10 физико-матем
Муниципальное образовательное учреждение «Гимназия №20» секция теоретической математики Автор: Буравлев Степан, 10 физико-матем Подготовка к ЕГЭ. Графическое решение уравнений и неравенств
Подготовка к ЕГЭ. Графическое решение уравнений и неравенств Франсуа Виет
Франсуа Виет Разложение квадратного трехчлена на множители
Разложение квадратного трехчлена на множители Метод Монте-Карло: моделирование дискретной случайной величины
Метод Монте-Карло: моделирование дискретной случайной величины Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Взаимные положения прямой и плоскости, двух плоскостей. Параллельность прямой и плоскости; двух плоскостей
Взаимные положения прямой и плоскости, двух плоскостей. Параллельность прямой и плоскости; двух плоскостей Логарифмические неравенства
Логарифмические неравенства Формулы сокращенного умножения. 7 класс
Формулы сокращенного умножения. 7 класс Готовимся к Всероссийским проверочным работам по математике
Готовимся к Всероссийским проверочным работам по математике Разгадать ребус
Разгадать ребус Показатели вариации
Показатели вариации Нормальний закон розподілу у сукупностях
Нормальний закон розподілу у сукупностях Презентация по математике "Пифагор. За легендой - Истина" - скачать
Презентация по математике "Пифагор. За легендой - Истина" - скачать  Дружественные, фигурные и совершенные числа, теория чисел
Дружественные, фигурные и совершенные числа, теория чисел Измерение углов на местности
Измерение углов на местности Арккосинус. Решение уравнения cos x=a
Арккосинус. Решение уравнения cos x=a Решение задач на применение первого признака равенства треугольников
Решение задач на применение первого признака равенства треугольников Задачи по геометрии
Задачи по геометрии