Functions of Random Variables 2. Method of Distribution Functions

Method of Distribution Functions

X1,…,Xn ~ f(x1,…,xn)
U=g(X1,…,Xn) – Want to obtain fU(u)
Find

Example – Uniform X

Stores located on a linear city with density

Example – Sum of Exponentials

X1, X2 independent Exponential(θ)
f(xi)=θ-1e-xi/θ xi>0, θ>0, i=1,2
f(x1,x2)=

Method of Transformations

X~fX(x)
U=h(X) is either increasing or decreasing in X
fU(u) =

Example

fX(x) = 2x 0≤ x ≤ 1, 0 otherwise
U=10+500X (increasing in

Method of Conditioning

U=h(X1,X2)
Find f(u|x2) by transformations (Fixing X2=x2)
Obtain the joint density

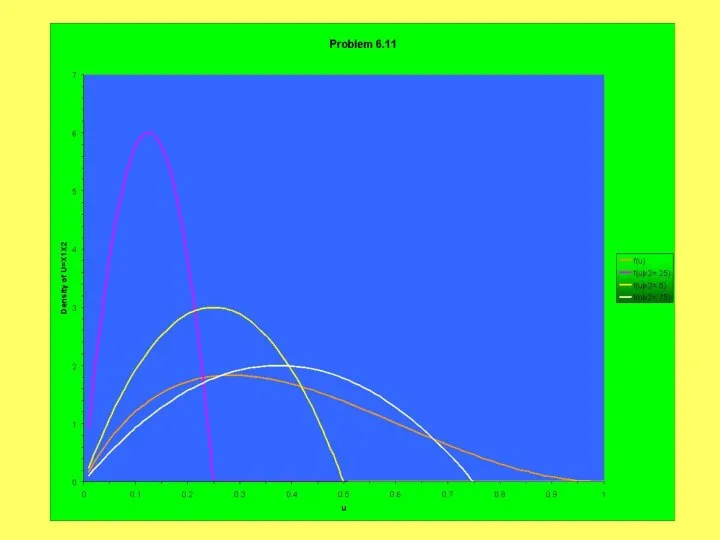
Example (Problem 6.11)

X1~Beta(α=2,β=2) X2~Beta(α=3,β=1) Independent
U=X1X2
Fix X2=x2 and get f(u|x2)

Method of Moment-Generating Functions

X,Y are two random variables
CDF’s: FX(x) and FY(y)
MGF’s:

Sum of Independent Gammas

Linear Function of Independent Normals

Distribution of Z2 (Z~N(0,1))

Distributions of and S2 (Normal data)

Independence of and S2 (Normal Data)

Independence of T=X1+X2 and D=X2-X1 for

Independence of and S2 (Normal Data) P2

Independence of T=X1+X2 and D=X2-X1

Distribution of S2 (P.1)

Distribution of S2 P.2

Summary of Results

X1,…Xn ≡ random sample from N(μ, σ2) population
In practice,

Order Statistics

X1,X2,...,Xn ≡ Independent Continuous RV’s
F(x)=P(X≤x) ≡ Cumulative Distribution Function
f(x)=dF(x)/dx ≡

Order Statistics

Example

X1,...,X5 ~ iid U(0,1)
(iid=independent and identically distributed)

Distributions of Order Statistics

Consider case with n=4
X(1) ≤x can be one

Case with n=4

General Case (Sample of size n)

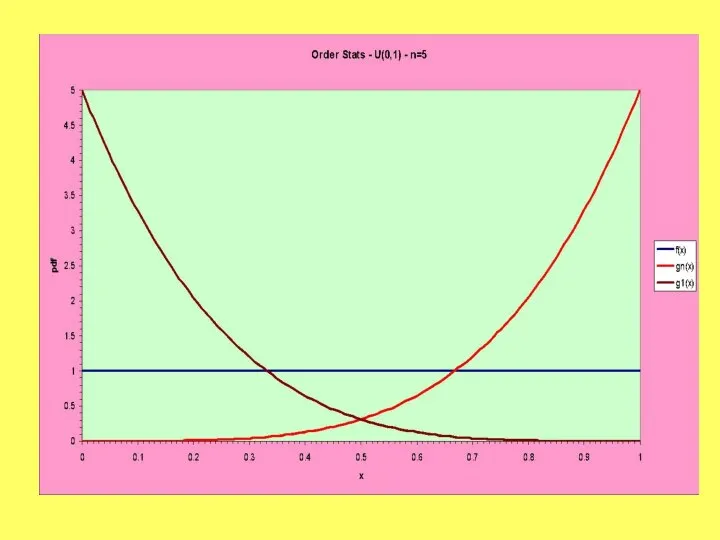
Example – n=5 – Uniform(0,1)