Содержание
- 2. Топологическая сортировка Определение. Частичным порядком на множестве А называется отношение R, определенное на А и такое,
- 3. Примеры частичного порядка: решение большой задачи разбивается на ряд подзадач, над которыми установлен частичный порядок: без
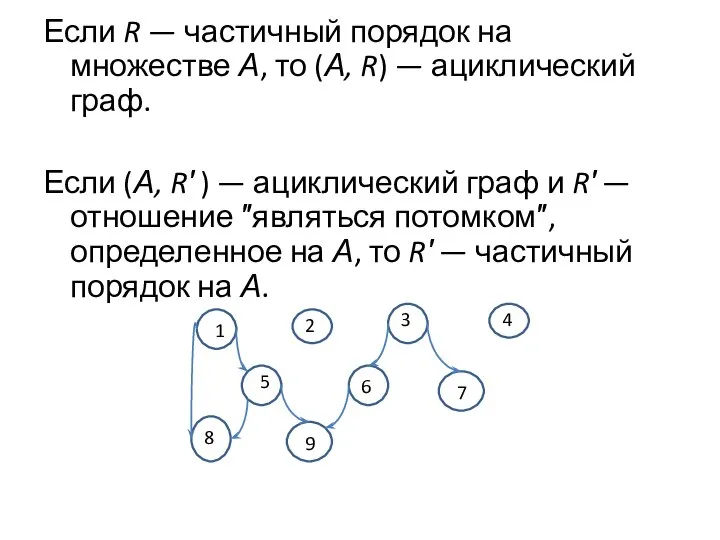
- 4. Если R — частичный порядок на множестве А, то (А, R) — ациклический граф. Если (А,
- 5. Определение. Линейный порядок R на множестве А — это такой частичный порядок, что если a и
- 6. Если задан частичный порядок R на множестве А, часто бывает нужен линейный порядок, содержащий этот частичный
- 7. 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7
- 8. Алгоритм. Топологическая сортировка Вход. Частичный порядок R на конечном множестве А. Выход. Линейный порядок R' на
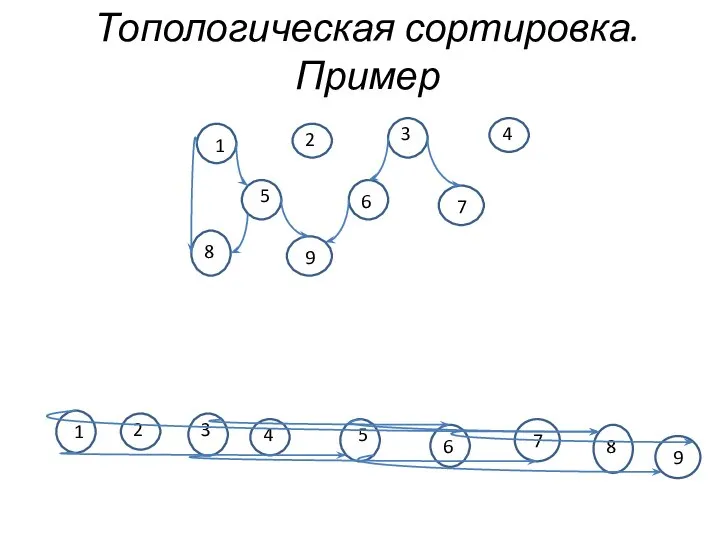
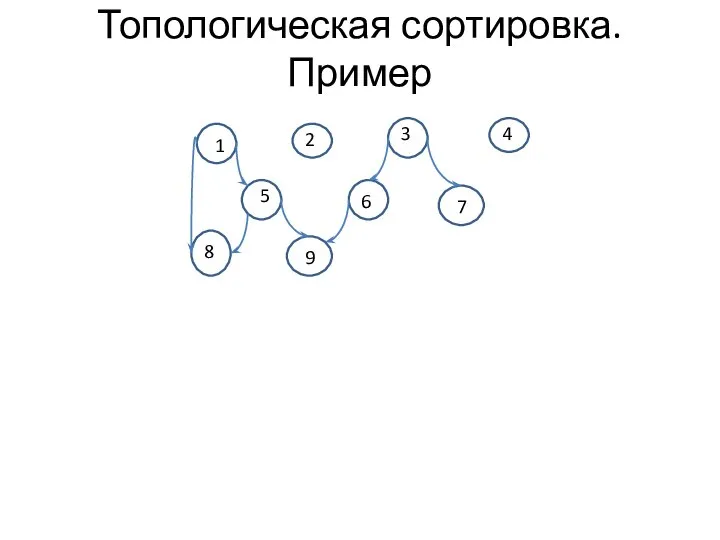
- 9. Топологическая сортировка. Пример 1 2 3 4 5 6 7 8 9
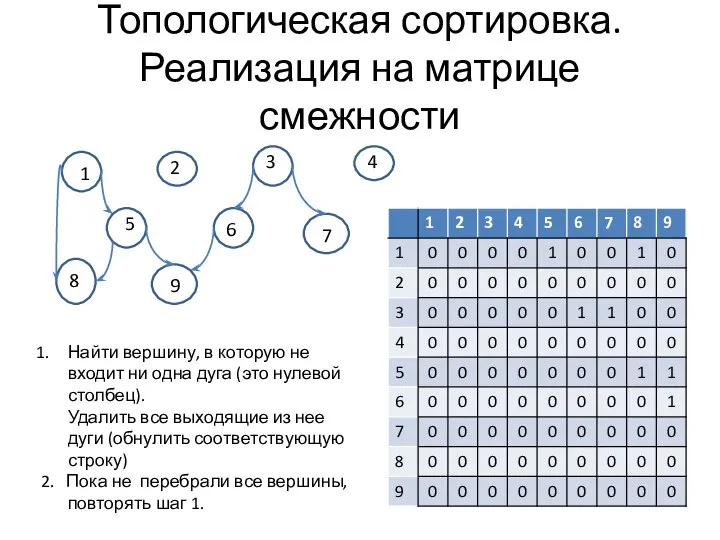
- 10. Топологическая сортировка. Реализация на матрице смежности 1 2 3 4 5 6 7 8 9 Найти
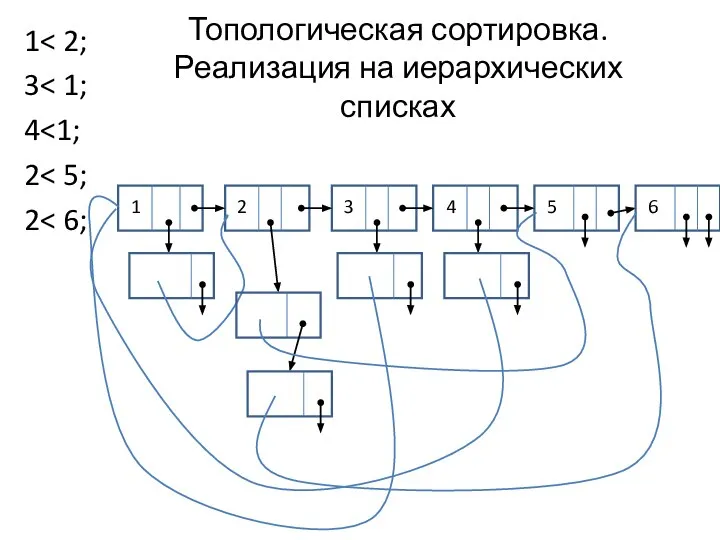
- 11. Топологическая сортировка. Реализация на иерархических списках 1 3 4 2 2 1 2 3 4 5
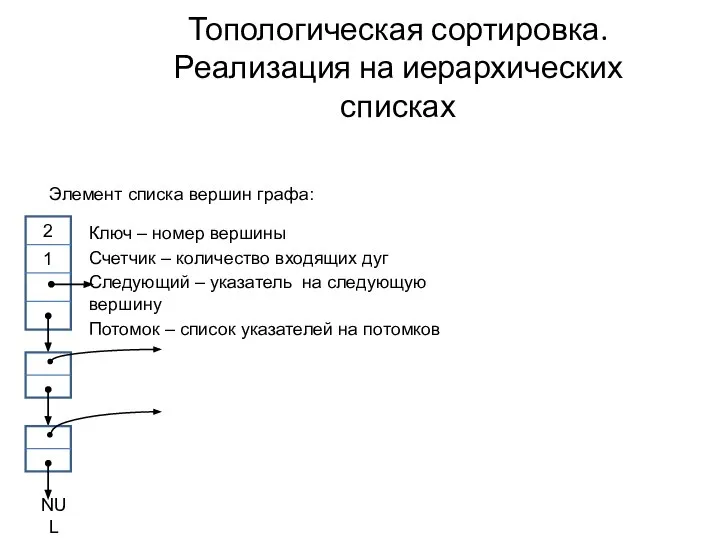
- 12. Топологическая сортировка. Реализация на иерархических списках 2 1 Ключ – номер вершины Счетчик – количество входящих
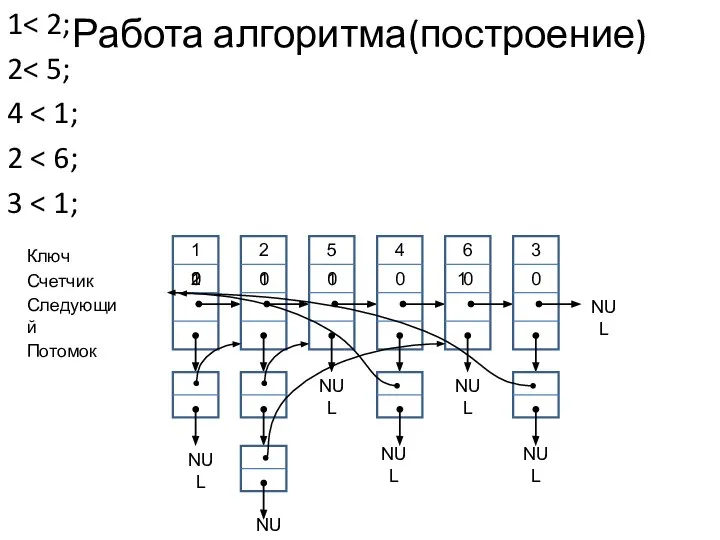
- 13. Работа алгоритма(построение) 1 2 2 1 5 1 4 0 6 1 3 0 Ключ Счетчик
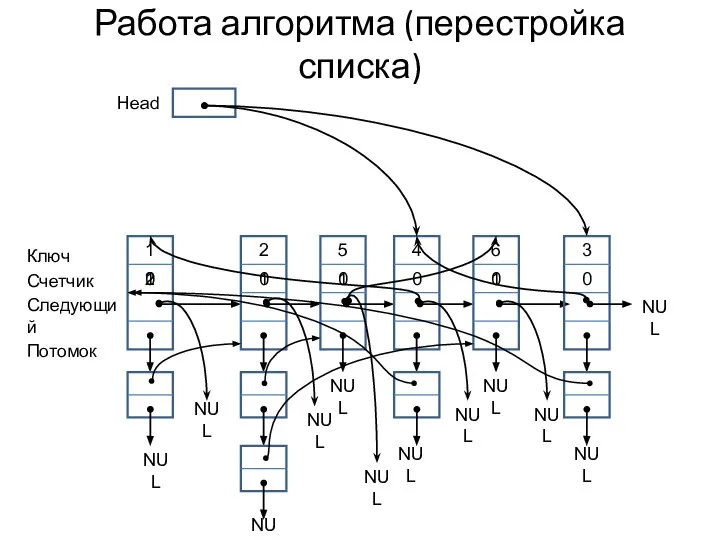
- 14. Работа алгоритма (перестройка списка) 1 2 2 1 5 1 4 0 6 1 3 0
- 15. Кратчайшие пути Пусть G = (V, E) – ориентированный граф. Поставим в оответствие каждому ребру e∈E
- 16. Ребра отрицательного веса Веса ребер могут ребер могут быть отрицательными. Важно знать, имеются ли циклы отрицательного
- 17. Пусть G = (V, E) – заданный граф. Для каждой вершины v ∈ V мы будем
- 18. Идея алгоритма нахождения кратчайших путей из одной вершины во все другие Строится множество S, содержащее вершины
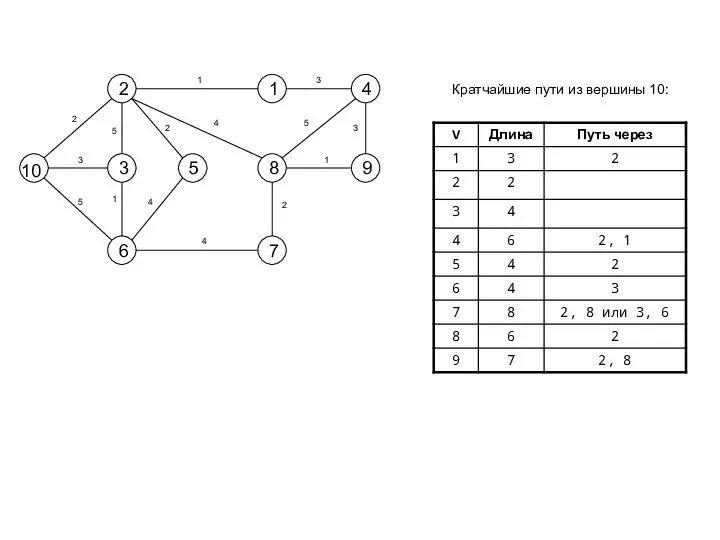
- 19. Кратчайшие пути из вершины 10: 10
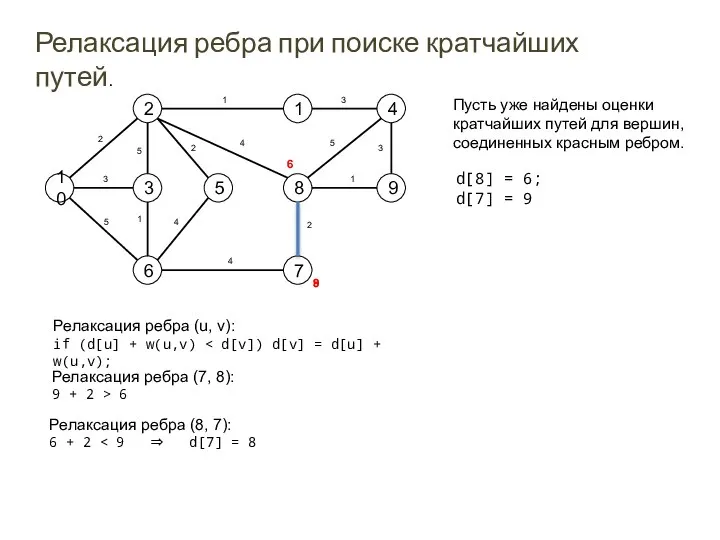
- 20. Техника релаксации Для каждого ребра (u,v) храним d[v] – верхнюю оценку кратчайшего пути из s в
- 21. Релаксация ребра (u,v): значение d[v] уменьшается до d[v+w(u,v)] (если второе значение меньше первого) Relax (u, v,
- 22. Релаксация ребра при поиске кратчайших путей. 10 2 3 6 1 8 5 7 4 9
- 23. В ходе работы алгоритма поддерживается множество S, состоящее из вершин, для которых δ(s,v) уже найдено (
- 24. Алгоритм Дейкстры Dijkstra(G,w,s){ Initialize(G,s); S ← ø; Q ← V; //очередь с приоритетами While (Q ≠
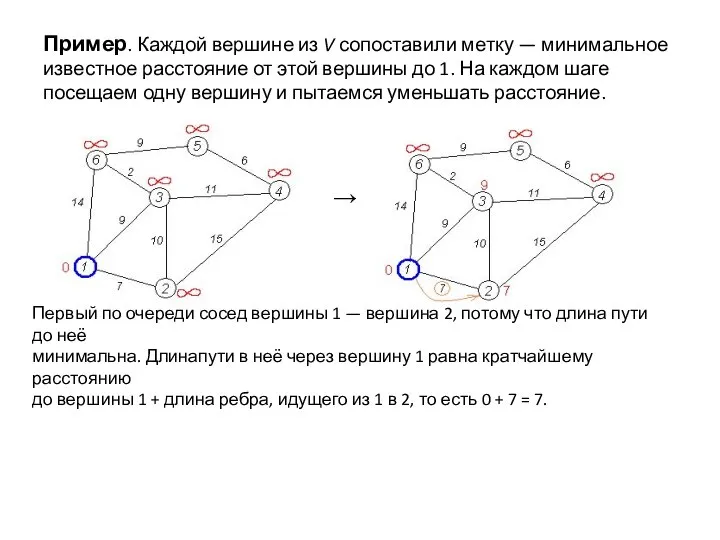
- 25. Пример. Каждой вершине из V сопоставили метку — минимальное известное расстояние от этой вершины до 1.
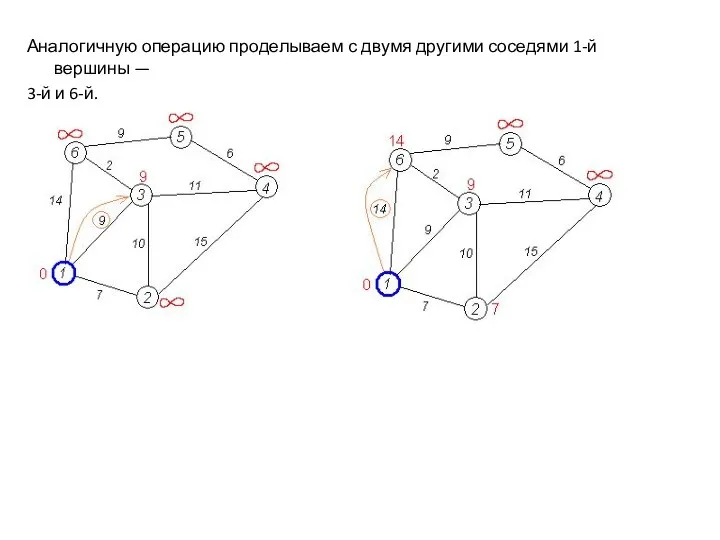
- 26. Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
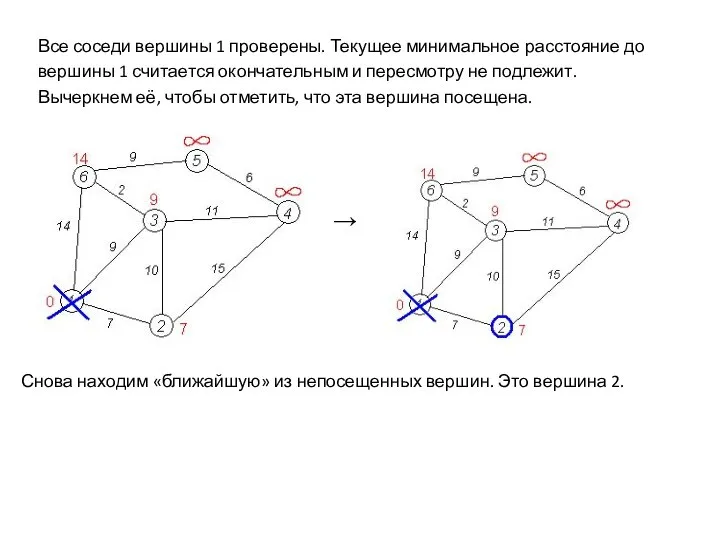
- 27. Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не
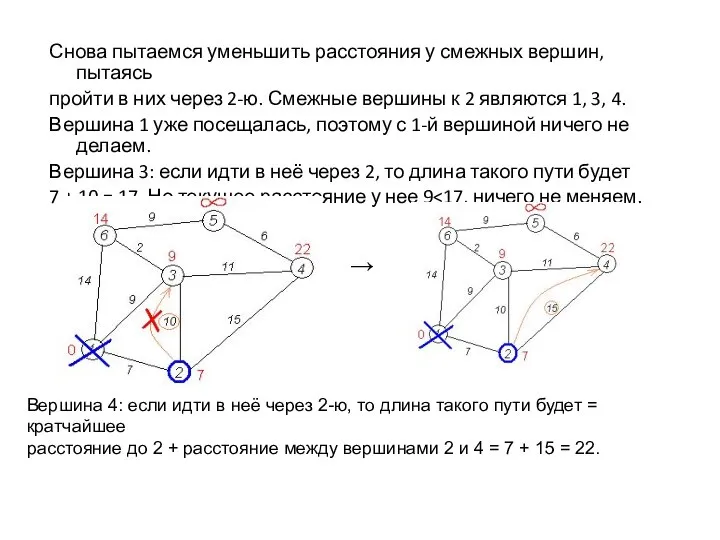
- 28. Снова пытаемся уменьшить расстояния у смежных вершин, пытаясь пройти в них через 2-ю. Смежные вершины к
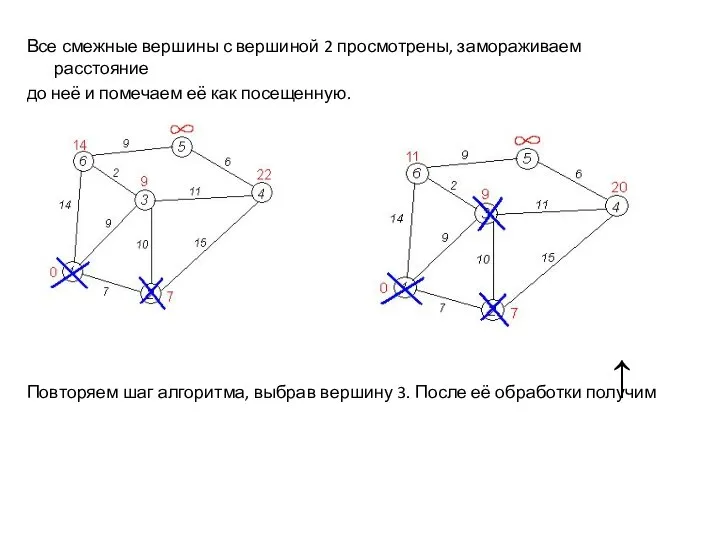
- 29. Все смежные вершины с вершиной 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную.
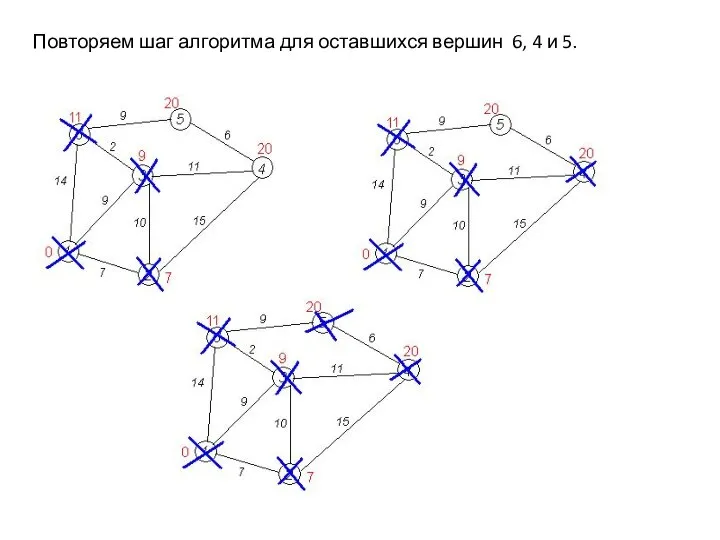
- 30. Повторяем шаг алгоритма для оставшихся вершин 6, 4 и 5.
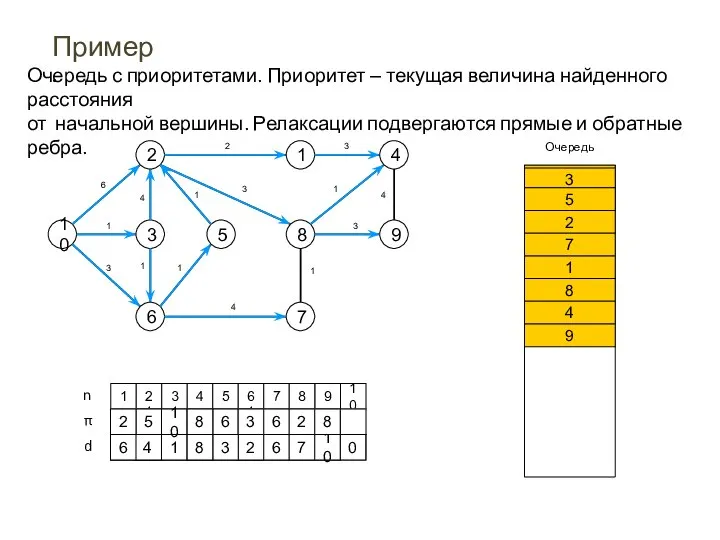
- 31. Пример. Очередь с приоритетами. Приоритет – текущая величина найденного расстояния от начальной вершины. Релаксации подвергаются прямые
- 32. Реализация с дополнительным массивом - O(n2) Массив D[v] содержит стоимость текущего кратчайшего пути из s в
- 33. Dijkstra { S ← {s}; D[s] ← 0; для всех v ∈V \ {v0} выполнить: D[v]
- 34. Пример № S u D[u] D[1] D[2] D[3] D[4] 0 {0} - - 2 +∞ +∞
- 35. Сложность алгоритма Дейкстры зависит от способа нахождения вершины v, а также способа хранения множества непосещенных вершин
- 36. * Если для хранения непосещенных вершин использовать фибоначчиеву кучу, для которой удаление происходит в среднем за
- 37. Алгоритм Беллмана — Форда За время O(n × m) алгоритм находит кратчайшие пути от одной вершины
- 38. Компьютерная сеть была названа ARPANET, все работы финансировались за счёт Министерства обороны США. Затем сеть ARPANET
- 39. Идея алгоритма Алгоритм позволяет очень просто определить, существует ли в графе G отрицательный цикл, достижимый из
- 40. Bellman-Ford(G,w,s) { Initialize(G,s); for(i=1; i for(∀ (u,v) ∈ E ) Relax(u,v,w); for(∀ (u,v) ∈ E )
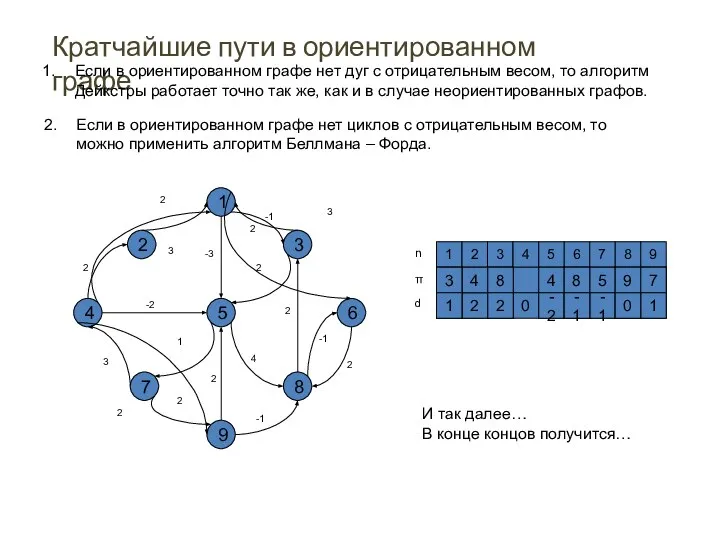
- 41. Кратчайшие пути в ориентированном графе Если в ориентированном графе нет дуг с отрицательным весом, то алгоритм
- 42. Нахождение кратчайших путей между всеми парами вершин Строим матрицу стоимостей: w(i, j), если ребро (i, j)∈E
- 43. Алгоритм Флойда-Уоршолла Обозначим через dij(k) стоимость кратчайшего пути из вершины с номером i в вершину с
- 44. Floyd-Warshall(M, n) { D(0) ← M; for k ← 1 to n do for i ←1
- 45. Транзитивное замыкание графа Пусть G= (V, E) ориентированный граф. Транзитивным замыканием графа G называется граф G’=
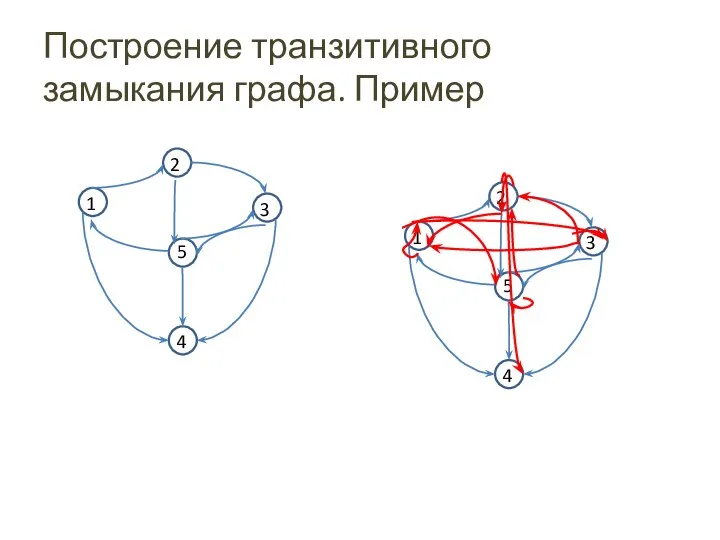
- 46. Построение транзитивного замыкания графа. Пример 1 3 2 5 4 1 3 2 5 4
- 47. Обозначим через tij(k) наличие пути из вершины с номером i в вершину с номером j с
- 48. Алгоритм построения транзитивного замыкания графа Tranzitive_Closure(M, n) { T(0) ← M; for k ← 1 to
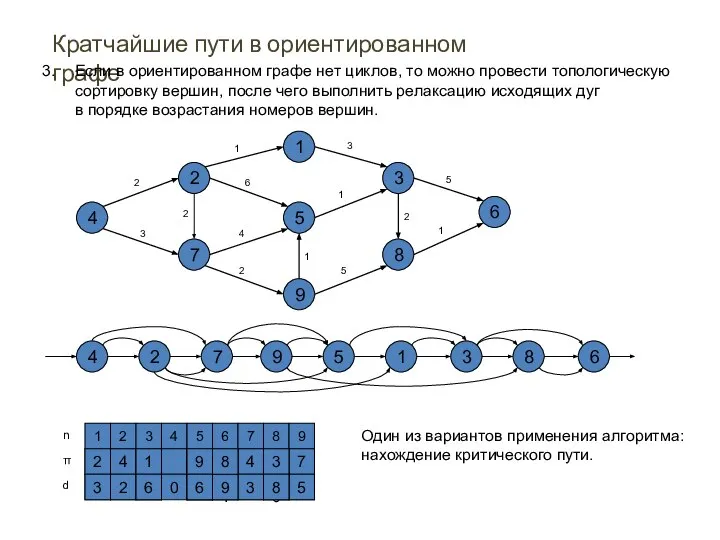
- 49. Кратчайшие пути в ориентированном графе Если в ориентированном графе нет циклов, то можно провести топологическую сортировку
- 51. Скачать презентацию









![Техника релаксации Для каждого ребра (u,v) храним d[v] – верхнюю оценку](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/649322/slide-19.jpg)
![Релаксация ребра (u,v): значение d[v] уменьшается до d[v+w(u,v)] (если второе значение](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/649322/slide-20.jpg)


![Реализация с дополнительным массивом - O(n2) Массив D[v] содержит стоимость текущего](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/649322/slide-31.jpg)
![Dijkstra { S ← {s}; D[s] ← 0; для всех v](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/649322/slide-32.jpg)
![Пример № S u D[u] D[1] D[2] D[3] D[4] 0 {0}](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/649322/slide-33.jpg)








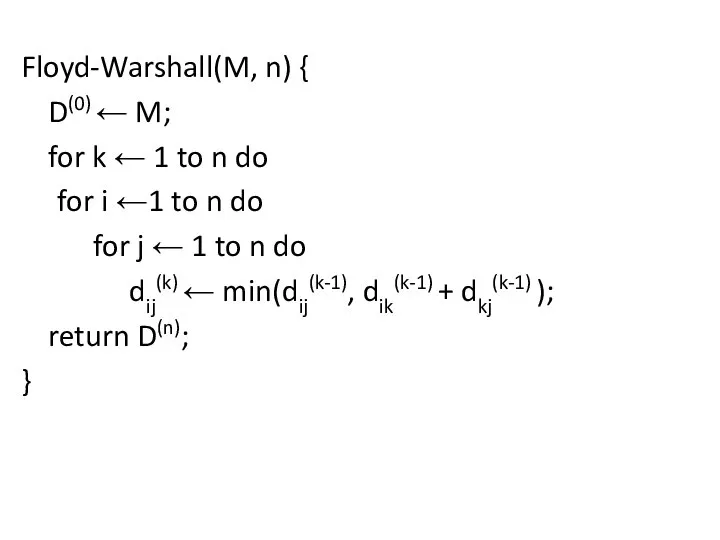



 Принципы решения слабоструктурированных проблем
Принципы решения слабоструктурированных проблем Теорема Пифагора
Теорема Пифагора Геометрические фигуры
Геометрические фигуры Игра- тренажёр по математике «Уроки с Мальвиной». Табличное умножение и деление
Игра- тренажёр по математике «Уроки с Мальвиной». Табличное умножение и деление Значение математики в информатике
Значение математики в информатике Есептер: Куб
Есептер: Куб Забавная математика
Забавная математика Влияние коэффициентов на расположение параболы. Выполнила: Дегтярева Анастасия Ученица 10 класса МОУ «Тарская СОШ №4» Руководит
Влияние коэффициентов на расположение параболы. Выполнила: Дегтярева Анастасия Ученица 10 класса МОУ «Тарская СОШ №4» Руководит Уравнения и неравенства с двумя переменными
Уравнения и неравенства с двумя переменными Обыкновенные дроби
Обыкновенные дроби Случаи вычитания 15 -
Случаи вычитания 15 - Мешко Іван Васильович Мешко І.В.
Мешко Іван Васильович Мешко І.В. Понятие множества. Способы задания множеств. Операции над множествами
Понятие множества. Способы задания множеств. Операции над множествами Скрещивающиеся прямые
Скрещивающиеся прямые Презентация по математике "Табличное сложение в пределах 10" - скачать
Презентация по математике "Табличное сложение в пределах 10" - скачать  Урок объяснения нового материала. Математика. 5 класс
Урок объяснения нового материала. Математика. 5 класс Комбинаторика. Общие правила комбинаторики
Комбинаторика. Общие правила комбинаторики Пример Ссуда в размере 1млн. рублей выдана 20 января до 5 октября включительно под простые проценты 18% годовых. Какую сумму должен
Пример Ссуда в размере 1млн. рублей выдана 20 января до 5 октября включительно под простые проценты 18% годовых. Какую сумму должен  Несобственный интеграл
Несобственный интеграл Рационал сандарды көбейту
Рационал сандарды көбейту Конкретизация вида коэффициента эффективной квадратичной нелинейной восприимчивости
Конкретизация вида коэффициента эффективной квадратичной нелинейной восприимчивости Реализация алгоритма ветвления на QBASIC. Задачи на повторение
Реализация алгоритма ветвления на QBASIC. Задачи на повторение Понятие множества
Понятие множества Аттестационная работа. Исследовательская деятельность старшеклассников на уроках математики как средство развития УУД
Аттестационная работа. Исследовательская деятельность старшеклассников на уроках математики как средство развития УУД Правильные многоугольники в нашей жизни
Правильные многоугольники в нашей жизни Задачи на готовых чертежах (Теорема Пифагора)
Задачи на готовых чертежах (Теорема Пифагора) 20160919_zadachi_aksiom_geometrii
20160919_zadachi_aksiom_geometrii Меньше или больше
Меньше или больше