Содержание
- 2. Свойства функции распределения: 1. 0≤ F(x)≤1 2. F(x2) > F(x1), если x2 > x1 Следствие 1.
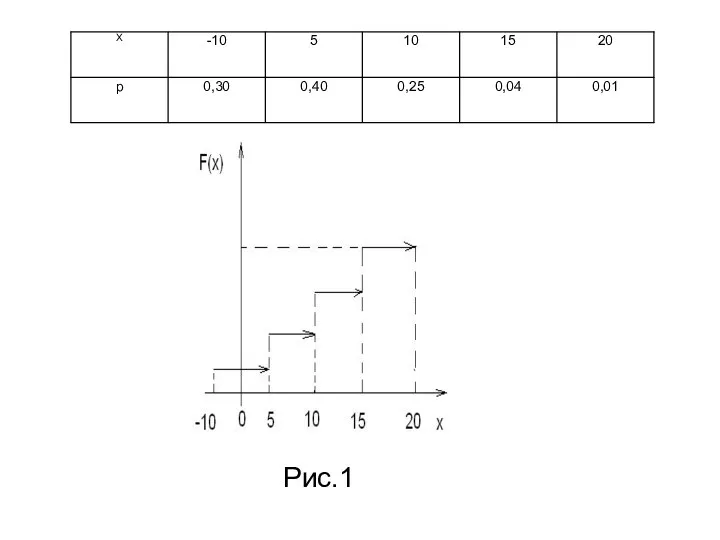
- 3. Для наглядности функцию распределения F(x) представляют в виде графика. Функция распределения F(x) в общем случае представляет
- 4. где хi Т.о., функция распределения любой дискретной случайной величины всегда есть разрывная ступенчатая функция, скачки которой
- 5. Рис.1
- 6. Пример. Брошена игральная кость. Случайная величина X –число выпавших очков. Написать закон распределения величины X и
- 7. Решение. Случайная величина X принимает возможные значения: {1, 2, 3, 4, 5, 6}. Вероятности этих значений
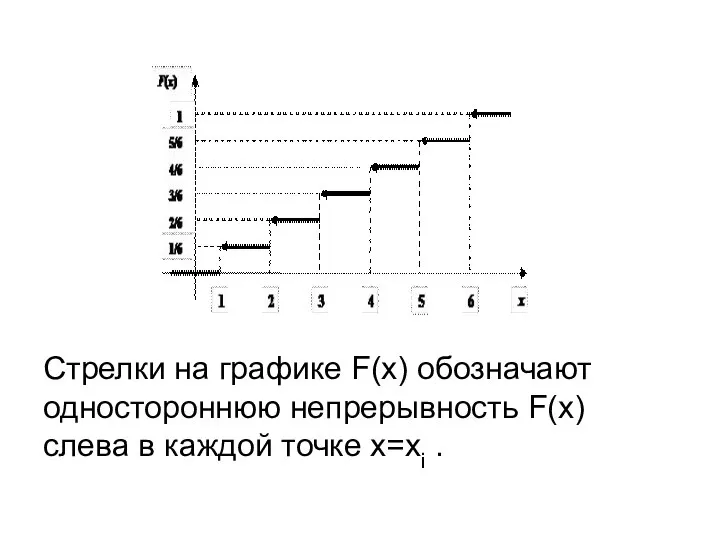
- 10. Стрелки на графике F(x) обозначают одностороннюю непрерывность F(x) слева в каждой точке x=xi .
- 11. §3.4. Плотность распределения случайной величины от х до х+Δх Р(х ≤ Х Рассмотрим отношение этой вероятности
- 12. Свойства плотности распределения. 1. р(х)≥0. р(х)=F(x)≥0 F(x)= 2. (-∞≤Х≤∞). 3. F(x)=
- 13. 4. [a, b) P(a≤X
- 14. Вместо закона или функции распределения для описания СВ используется также так называемая характеристическая функция (ХФ). ХФ
- 15. где u – вещественная переменная, i= - мнимая единица. Для распределения, обладающего плотностью р(х), ХФ является
- 16. §3.5. Квантили При решении практических задач часто требуется найти значение x, при котором функция распределения Fx(x)
- 17. α-квантиль (квантиль порядка α) – это числовая характеристика закона распределения случайной величины. α-квантиль – такое число,
- 18. Данные условия эквивалентны следующим: P(X xα)≥ 1 – α . Если F(X)– непрерывная строго монотонная функция,
- 19. Кроме рассмотренного случая, когда уравнение F(xα) = α имеет единственное решение и дает соответствующий квантиль, возможны
- 20. – уравнение F(xα) = α имеет более одного решения. Значит, все его решения образуют интервал, на
- 21. Если возникает необходимость отделить сверху, снизу или с обеих сторон области, вероятности попадания в которые малы,
- 22. Квантилью α (α – квантилью, квантилью уровня α) случайной величины Х, имеющей функцию распределения F(x), называют
- 23. Квантили, наиболее часто встречающиеся в практических задачах, имеют свои названия: – медиана – квантиль уровня 0.5
- 24. Если же оно расположено там, где находятся верхние 25% значений, то говорят, что оно расположено в
- 26. Скачать презентацию









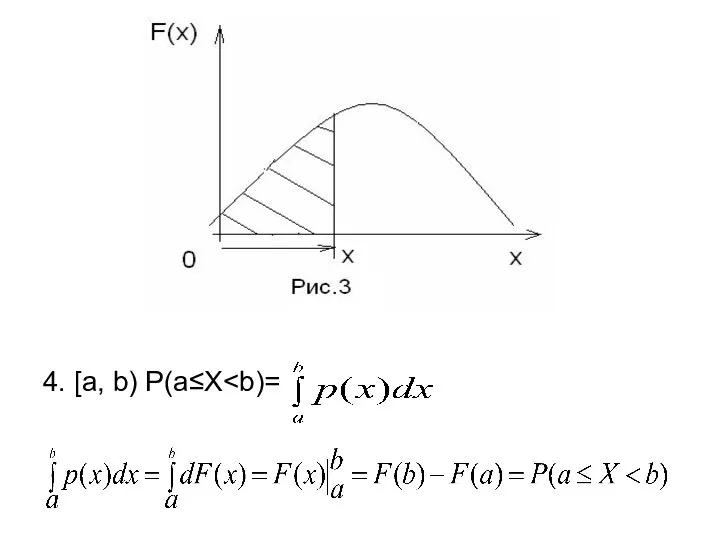











 Математика 1 класс "Школа 2100"
Математика 1 класс "Школа 2100" Комплексные чертежи прямых линий
Комплексные чертежи прямых линий Урок математики
Урок математики  Разность квадратов Артамонова Л.В., Учитель математики
Разность квадратов Артамонова Л.В., Учитель математики  Математическое развитие детей в семье
Математическое развитие детей в семье Это забавные животные. Занимательные задачи
Это забавные животные. Занимательные задачи Полный дифференциал функции нескольких переменных
Полный дифференциал функции нескольких переменных Проверка статистических гипотез
Проверка статистических гипотез Сложение и вычитание десятичных дробей. (Урок 112)
Сложение и вычитание десятичных дробей. (Урок 112) Логарифмическая функция. Свойства, график
Логарифмическая функция. Свойства, график Математическое моделирование в различных областях знания
Математическое моделирование в различных областях знания Векторні величини. Метод координат
Векторні величини. Метод координат Дискретная математика
Дискретная математика «Больше дела – меньше слов»
«Больше дела – меньше слов»  Закон распределения случайной дискретной величины
Закон распределения случайной дискретной величины Урок на тему: Теорема Фалеса Автор: Дятченко Татьяна Юрьевна Учитель математики ГОУ СОШ № 15
Урок на тему: Теорема Фалеса Автор: Дятченко Татьяна Юрьевна Учитель математики ГОУ СОШ № 15  Отношения и пропорции
Отношения и пропорции Окружность и круг
Окружность и круг Неравенства. Знаки «< », «>»
Неравенства. Знаки «< », «>» Урок - морское путешествие. Дробные выражения
Урок - морское путешествие. Дробные выражения Задачи на чётность Медведев Михаил ученик 6 Б класса МОУ «СОШ № 19 с углубленным изучением предметов физико-математического пр
Задачи на чётность Медведев Михаил ученик 6 Б класса МОУ «СОШ № 19 с углубленным изучением предметов физико-математического пр Operation with Desimal Fractions
Operation with Desimal Fractions Отыскание наибольшего и наименьшего значений непрерывной функции на промежутке
Отыскание наибольшего и наименьшего значений непрерывной функции на промежутке Тhe first wonderful limit
Тhe first wonderful limit Симметрия – вокруг нас Геометрия
Симметрия – вокруг нас Геометрия  Соотношения между тригонометрическими функциями одного и того же угла
Соотношения между тригонометрическими функциями одного и того же угла Элементы комбинаторики, статистики и теории вероятностей. Решение заданий В 10 ЕГЭ
Элементы комбинаторики, статистики и теории вероятностей. Решение заданий В 10 ЕГЭ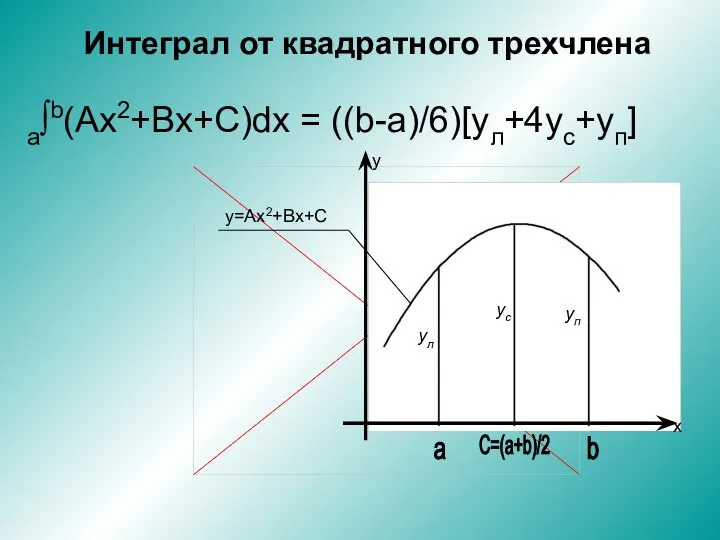 Интеграл от квадратного трехчлена
Интеграл от квадратного трехчлена