Функции нескольких переменных

1. ОСНОВНЫЕ ПОНЯТИЯ

Пусть имеется n переменных величин, и каждому набору

ПРИМЕР.

Функция

задает объем цилиндра z как функцию двух переменных:
х1 –

Переменные х1…хn называются независимыми
переменными.

Z называется зависимой переменной.

Множество Х называется областью
определения

ПРИМЕРЫ.

1

Найти область определения функции:

РЕШЕНИЕ.

Поэтому областью определения является круг с центром в начале координат

2

Найти область определения функции:

РЕШЕНИЕ.

Поэтому областью определения является плоскость ОХ1Х2, за исключением координатных прямых

Рассмотрим примеры функций нескольких переменных.

1

Линейная функция

2

Квадратическая функция

3

Функция Кобба-Дугласа

В дальнейшем мы будем рассматривать частный случай функции нескольких переменных -

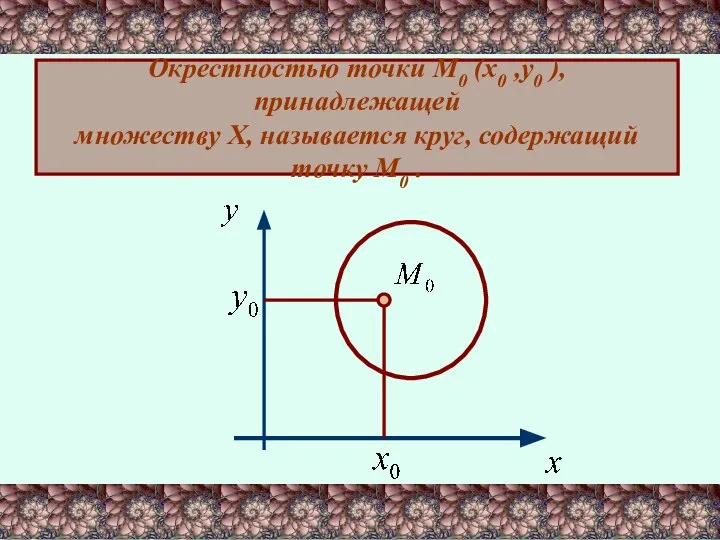
Окрестностью точки М0 (х0 ,у0 ), принадлежащей
множеству Х, называется круг, содержащий

Круг на плоскости есть двумерный аналог интервала на прямой.
Любой функции f(x,y)

имеют одинаковое происхождение, их вид может существенно отличаться.
Например, функция

является

Графиком функции двух переменных z=f(x,y)
называется множество точек трехмерного
пространства (x,y,z),

Для построение графика функции f(x,y) полезно рассмотреть функции одной переменной:
z=f(x0,y) и

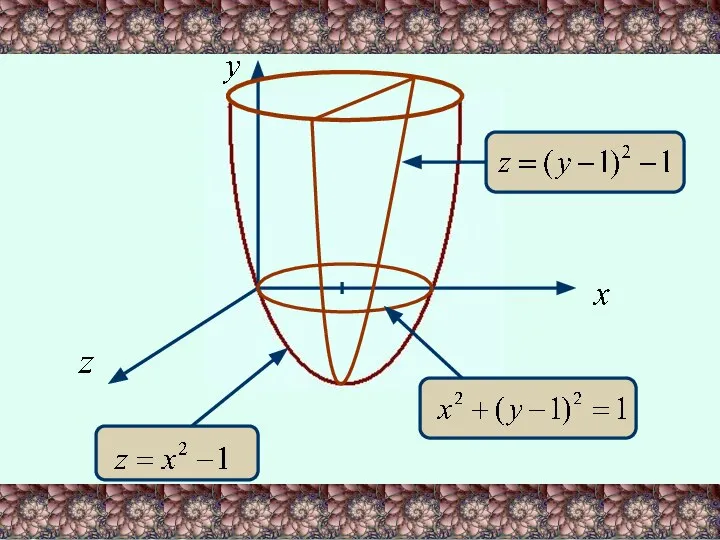
ПРИМЕР.

Построить график функции:

РЕШЕНИЕ.

Найдем сечения поверхности плоскостями, параллельными координатным плоскостям.
Для этого преобразуем функцию

При х=0 (сечение плоскостью YOZ):

- парабола

При z=0 (сечение плоскостью XOY):

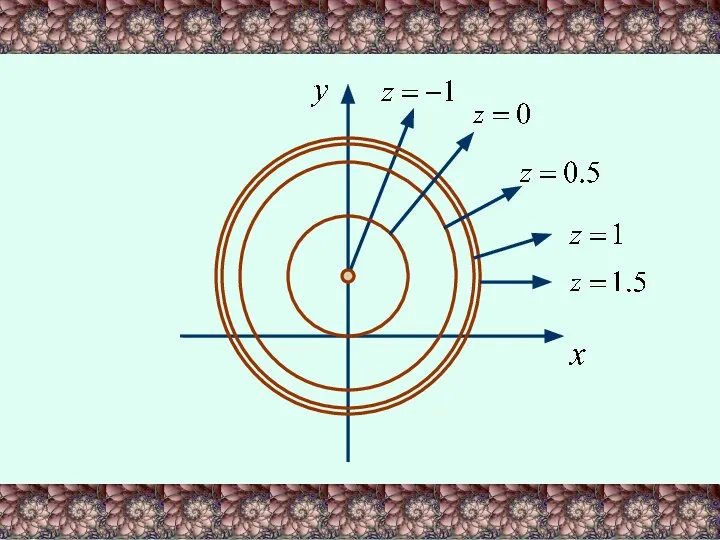
Линией уровня функции двух переменных
z=f(x,y) называется множество точек на
плоскости, таких

ПРИМЕР.

Построить линии уровня функции:

РЕШЕНИЕ.

Линия уровня z=C – это кривая на плоскости XOY, которая

Это будет окружность с центром в точке (0,1) и радиусом

При С=-1

Линия уровня позволяют представить график данной функции.
Расстояния между линиями с одинаковым

2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

Число А называется пределом

ПРИМЕР.

Вычислить предел функции,
когда оба аргумента
стремятся к нулю.

РЕШЕНИЕ.

Вычисление пределов функции одной переменной является менее сложной задачей, чем вычисление

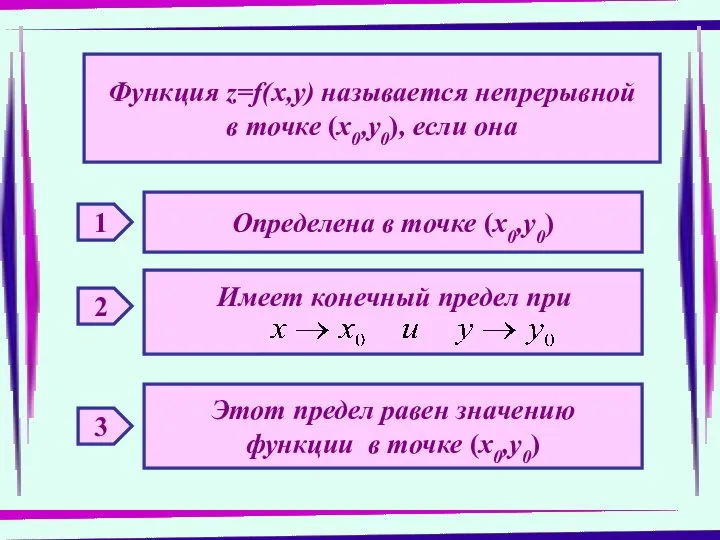
Функция z=f(x,y) называется непрерывной
в точке (х0,у0), если она

1

Определена в точке (х0,у0)