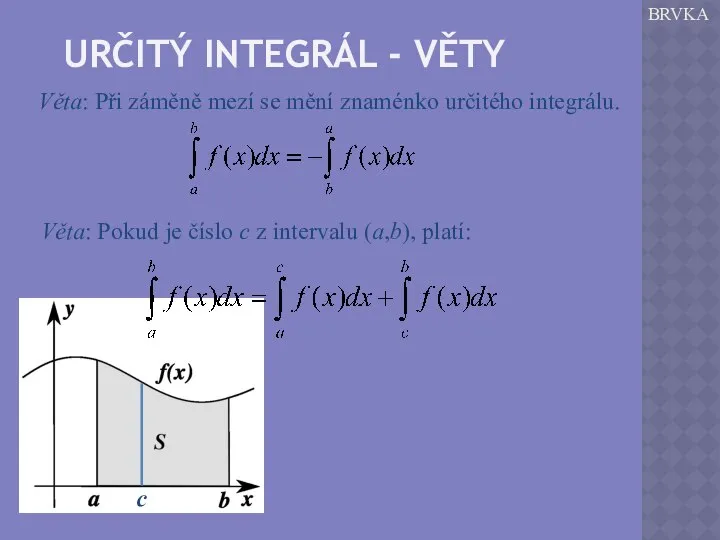
GEOMETRICKÝ VÝZNAM INTEGRÁLU
Geometrický význam integrálu je obsah plochy pod grafem funkce,
kterou integrujeme.
BRVKA
Plocha pod grafem funkce je ohraničena osou x, grafem funkce a svislými přímkami v bodech a, b.
Čím budou obdélníky užší, tím bude určení obsahu plochy pod grafem přesnější.
Pro přibližný výpočet můžeme plochu rozdělit na úzké obdélníky a plochu počítat jako jejich součet.
Pokud se bude šířka obdélníků blížit nule, bude se jejich součet limitně blížit obsahu plochy.
Určitý integrál chápeme jako limitu ze součtu obdélníků při jejich limitně se zužující šířce.




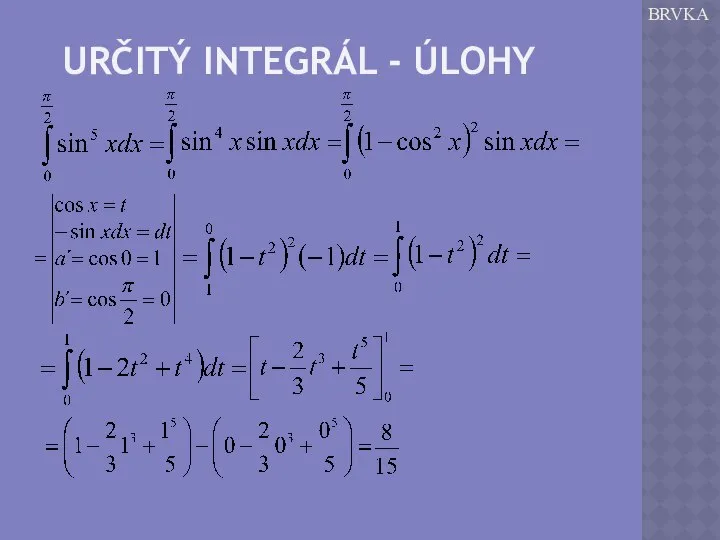

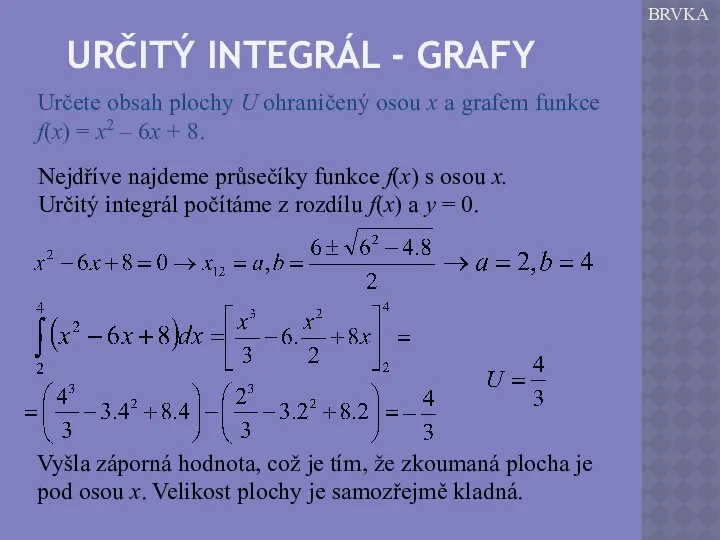
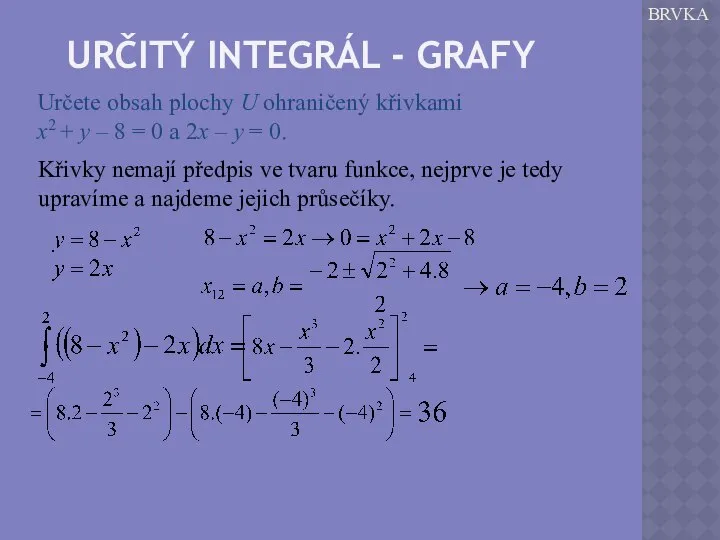

 Математическая физминутка
Математическая физминутка Вынесение общего множителя за скобки
Вынесение общего множителя за скобки Учебно-исследовательская работа «Многогранники»
Учебно-исследовательская работа «Многогранники» Презентация по математике "Семейная математика" - скачать
Презентация по математике "Семейная математика" - скачать  Производная и интеграл степенной функции с действительным показателем
Производная и интеграл степенной функции с действительным показателем Плоскость и прямая в пространстве
Плоскость и прямая в пространстве Поверхностные интегралы
Поверхностные интегралы Задачи на дроби
Задачи на дроби Графические методы оценки параметров распределения
Графические методы оценки параметров распределения Круги Эйлера
Круги Эйлера Метод координат
Метод координат Центральная симметрия
Центральная симметрия Виды углов. Измерение углов
Виды углов. Измерение углов Числовые и буквенные выражения
Числовые и буквенные выражения Наибольший общий делитель. Взаимно простые числа
Наибольший общий делитель. Взаимно простые числа Обыкновенные дроби
Обыкновенные дроби Магическое число Шехерезады
Магическое число Шехерезады Расстояние от точки до прямой
Расстояние от точки до прямой Презентация по математике "Решение показательных уравнений" -
Презентация по математике "Решение показательных уравнений" -  Аттестационная работа. Образовательная программа внеурочной деятельности. Создаем проекты по математики. (5 класс)
Аттестационная работа. Образовательная программа внеурочной деятельности. Создаем проекты по математики. (5 класс) Построение оценок производительности и эффективности параллельных компьютеров. Законы Адмала, Густавсона-Барсиса
Построение оценок производительности и эффективности параллельных компьютеров. Законы Адмала, Густавсона-Барсиса Метрология. Основные термины и определения. (Лекция 1)
Метрология. Основные термины и определения. (Лекция 1) Графический способ решения уравнений с модулем
Графический способ решения уравнений с модулем Математические преобразования в МР-томографии
Математические преобразования в МР-томографии Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Линейные дифференциальные уравнения n-го порядка (однородные с постоянными коэффициентами, уравнения Эйлера)
Линейные дифференциальные уравнения n-го порядка (однородные с постоянными коэффициентами, уравнения Эйлера) Презентация по математике "Применение формул сокращенного умножения к преобразованию выражений" -
Презентация по математике "Применение формул сокращенного умножения к преобразованию выражений" -  Устный счёт
Устный счёт