Содержание
- 2. План лекции Двумерное преобразование Фурье Преобразование Фурье Теорема о свертке Фильтрация изображений Преобразование Радона Преобразование Радона
- 3. Одномерное преобразование Фурье Прямое преобразование сигнал во времени в спектр по частоте Обратное преобразование переводит спектр
- 4. Двумерное преобразование Фурье Аналогично одномерному случаю – прямое преобразование И обратное преобразование
- 5. Двумерное дискретное преобразование Фурье Для дискретного набора данных – прямое преобразование И обратное преобразование
- 6. Двумерное преобразование Фурье Как и в случае одномерного преобразования Фурье, двумерное преобразование является сменой базиса разложения
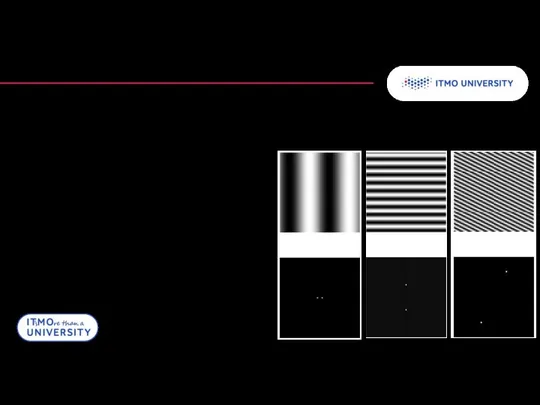
- 7. Изображение и его пространственный спектр Изображение Спектр Фильтр
- 8. Изображение и его пространственный спектр Изображение LP HP
- 9. Дискретная двумерная свертка Для двух дискретных функций свертка определяется, как Пределы суммирования могут варьироваться в зависимости
- 10. Связь свертки и преобразования Фурье Теорема о свертке
- 11. Свертка, как фильтр Так как результатом свертки является модификация каждого значения функции f, то операцию свертки
- 12. Ядро усреднения Рассмотрим действие ядра Из определения свертки – сопоставит значению функции значение, усредненное с 8
- 13. Ядро размытия Примеры действия ядра 3х3 9х9
- 14. Ядро усреднения по Гауссу Рассмотрим действие ядра При выборе большого σ – фильтр размытия (усреднения) При
- 15. Усреднение по Гауссу
- 16. Градиент (производная первого порядка) Ядро Превитта (в зависимости от направления взятия производной) Ядро Собеля
- 17. Ядро Превитта Примеры действия ядра dx dy
- 18. Ядро Собеля Примеры действия ядра dx dy
- 19. Лапласиан Сочетание двух производных второго порядка по двум координатам Форма – из численной аппроксимации второй производной
- 20. Лапласиан
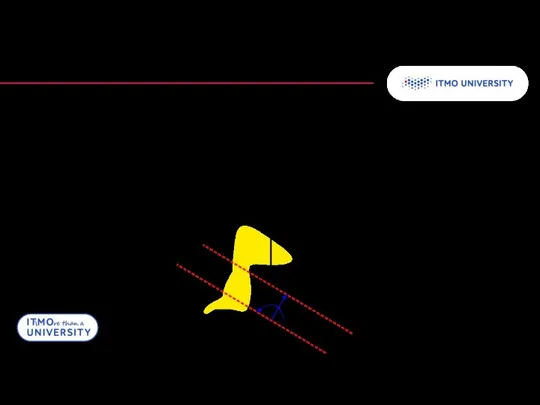
- 21. Преобразование Радона Прямое преобразование: переводит двумерную функцию в её интеграл вдоль произвольной оси r θ
- 22. Преобразование Радона Пример преобразования
- 23. Обратное преобразование Радона Обратное преобразование радона (алгоритм обратной проекции) И его дискретная модель
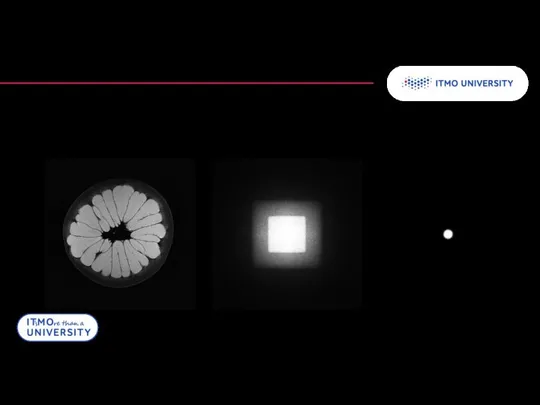
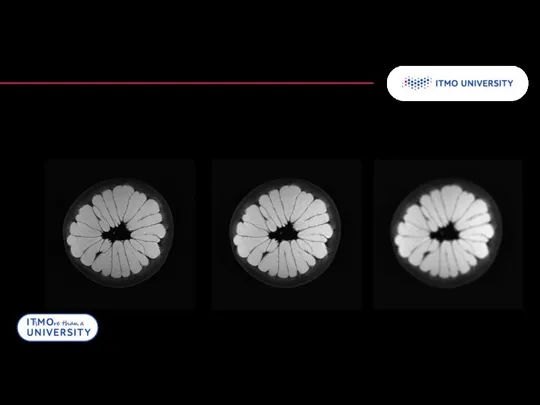
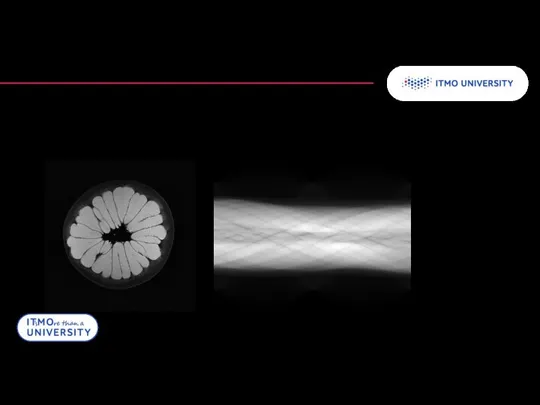
- 24. Обратное преобразование Радона Точность реконструкции зависит от числа проекций 5 12 180
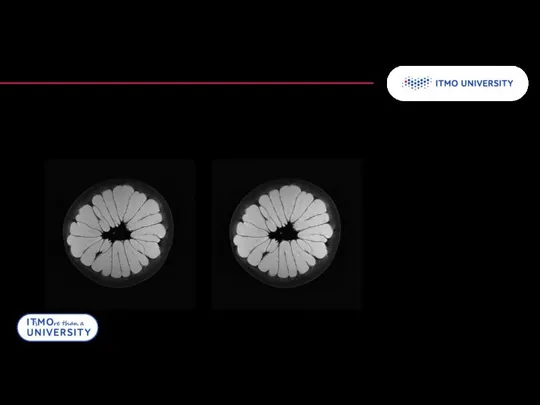
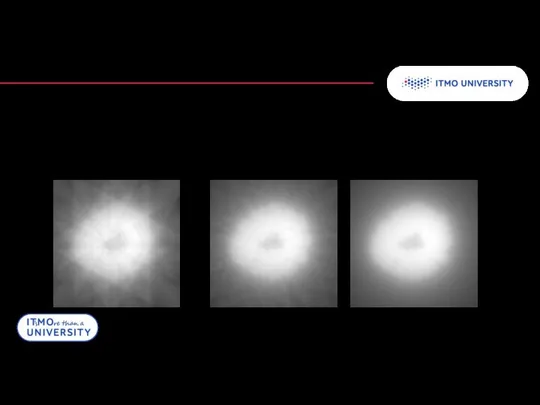
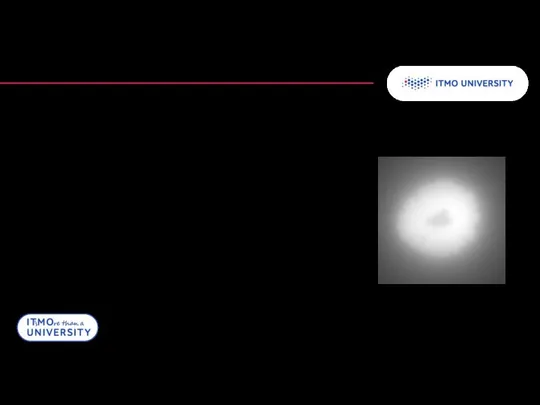
- 25. Обратное преобразование Радона Однако, даже при большом числе проекций реконструкция получается неточной Для точечного источника реконструкция
- 26. Теорема о центральном сечении Фурье-преобразование проекции функции на ось является Фурье-образом функции вдоль линии, проходящей через
- 27. Алгоритм отфильтрованной обратной проекции Предполагает реконструкцию исходного изображения из проекций, прошедших фильтрацию в частотном пространстве
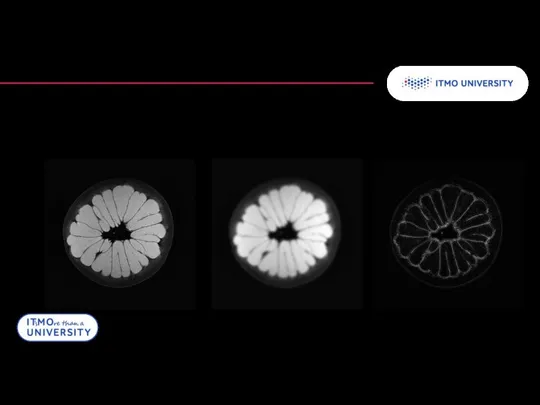
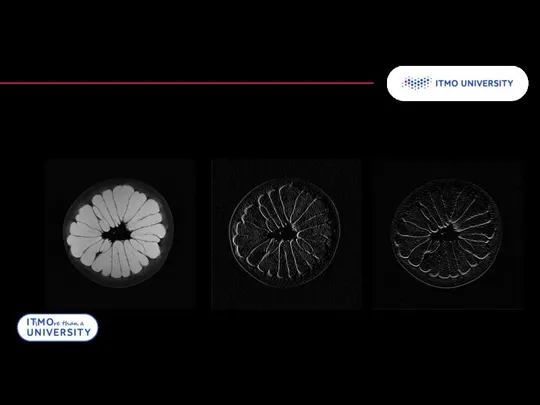
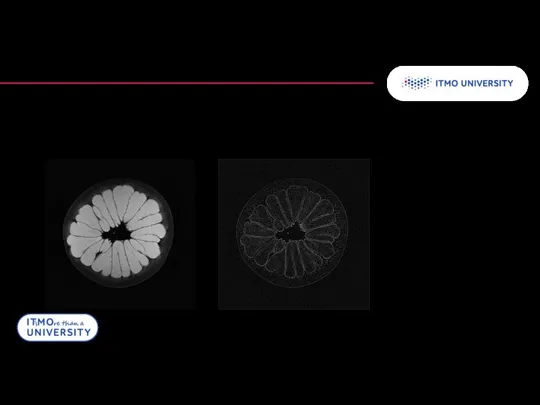
- 28. Алгоритм отфильтрованной обратной проекции Пример преобразования
- 30. Скачать презентацию















 Прямоугольный параллелепипед. Задача на сечение
Прямоугольный параллелепипед. Задача на сечение Деловая игра «Дизайнеры». Занятие на тему: «Паркеты из правильных многоугольников»
Деловая игра «Дизайнеры». Занятие на тему: «Паркеты из правильных многоугольников» Основы теории фракталов
Основы теории фракталов Презентация по математике "«Десятичные дроби» 6 класс" - скачать бесплатно
Презентация по математике "«Десятичные дроби» 6 класс" - скачать бесплатно Диаметр окружности
Диаметр окружности Решение уравнений (2 класс)
Решение уравнений (2 класс) Математический диктант по теме: Сечения конуса и цилиндра
Математический диктант по теме: Сечения конуса и цилиндра Решение простейших тригонометрических неравенств (10 класс)
Решение простейших тригонометрических неравенств (10 класс) Длина окружности и площадь круга. Решение задач. 9 класс
Длина окружности и площадь круга. Решение задач. 9 класс Отношение двух чисел. Работа с математической моделью
Отношение двух чисел. Работа с математической моделью Игра "Экология и математика"
Игра "Экология и математика" Презентация по математике "Стань отличником по математике" - скачать бесплатно
Презентация по математике "Стань отличником по математике" - скачать бесплатно Похідна функції, її геометричний та фізичний зміст
Похідна функції, її геометричний та фізичний зміст Презентация Прямоугольный параллелепипед
Презентация Прямоугольный параллелепипед  Асимптоты графика функции
Асимптоты графика функции Симметрия относительно точки
Симметрия относительно точки Показательные неравенства
Показательные неравенства Презентация по математике "Единицы площади урок" - скачать
Презентация по математике "Единицы площади урок" - скачать  Аттестационная работа. Образовательная программа внеурочной деятельности по математике в разновозрастной группе
Аттестационная работа. Образовательная программа внеурочной деятельности по математике в разновозрастной группе Логарифмическая функция
Логарифмическая функция Презентация по математике "Приключения мушкетеров. Решение логических задач" - скачать
Презентация по математике "Приключения мушкетеров. Решение логических задач" - скачать  Аттестационная работа. Методическая разработка «Математика и литература - два звена процесса творчества»
Аттестационная работа. Методическая разработка «Математика и литература - два звена процесса творчества»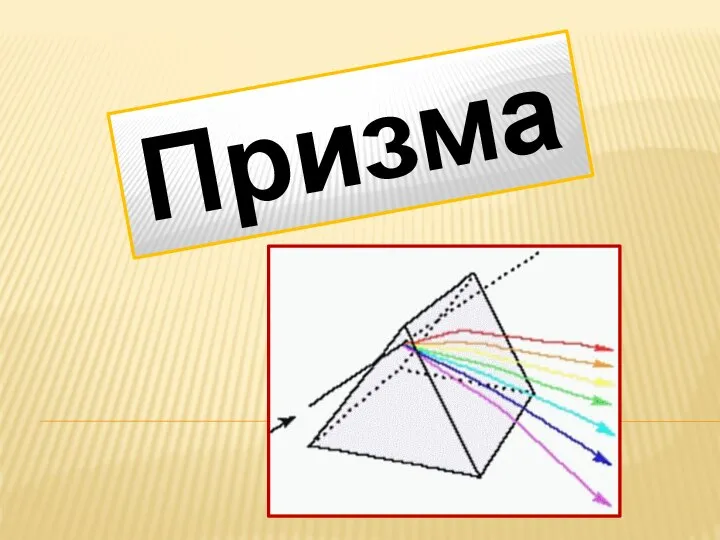 Призма. Дисперсия света в призме
Призма. Дисперсия света в призме Классическое определение вероятности
Классическое определение вероятности Применение компьютерных технологий
Применение компьютерных технологий Формулы сокращенного умножения
Формулы сокращенного умножения Сводка и группировка данных статистического наблюдения
Сводка и группировка данных статистического наблюдения Проценты. Процент от величины
Проценты. Процент от величины