Содержание
- 2. 20.1. ПОНЯТИЕ ПОВЕРХНОСТНОГО ИНТЕГРАЛА Понятие двойного интеграла по плоской области обобщается на случай интегрирования по поверхности.
- 3. Сумму вида называют интегральной суммой для функции f(x,y,z) по поверхности S.
- 4. Если существует конечный предел интегральной суммы при стремлении к 0 диаметра каждой площадки разбиения, не зависящий
- 5. Свойства поверхностных интегралов аналогичны свойствам двойных интегралов. Рассмотрим вычисление поверхностных интегралов. Пусть дан поверхностный интеграл и
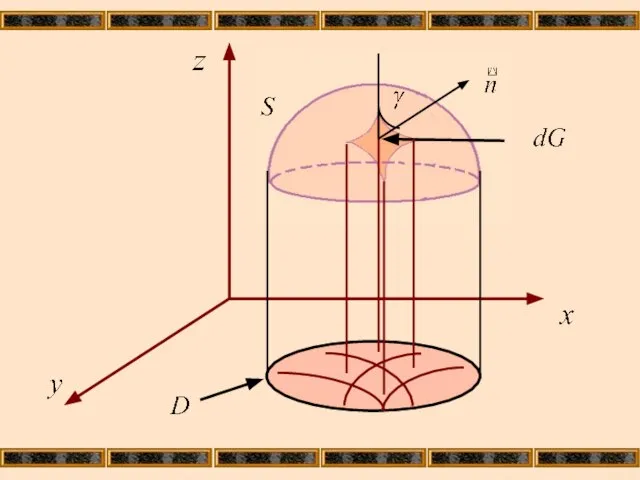
- 7. Выберем элемент площади dxdy плоскости D и проектирующийся в него элемент площади ΔG поверхности S. Проведем
- 9. Скачать презентацию





 Порядок выполнения действий в числовых выражениях. Урок 15
Порядок выполнения действий в числовых выражениях. Урок 15 Презентация по математике "Действия с десятичными дробями" - скачать
Презентация по математике "Действия с десятичными дробями" - скачать  Проценты. Решение задач
Проценты. Решение задач Методика изучения времени
Методика изучения времени Презентация на тему урок геометрии в 7 классе Искусство рассуждать
Презентация на тему урок геометрии в 7 классе Искусство рассуждать  Устный счёт
Устный счёт Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Matrices: Basic Operations
Matrices: Basic Operations Числовое и буквенное выражения
Числовое и буквенное выражения Презентация по математике "Функция у=ах^2, её свойства и график" - скачать бесплатно
Презентация по математике "Функция у=ах^2, её свойства и график" - скачать бесплатно Функция y=x^n
Функция y=x^n Устный счёт!
Устный счёт!  Яковлева Ксения ученица 11 класса МБОУ «СОШ№22» г. Анжеро-Судженск, Кемеровской области Научный руководитель: Лилия Геннадьевна
Яковлева Ксения ученица 11 класса МБОУ «СОШ№22» г. Анжеро-Судженск, Кемеровской области Научный руководитель: Лилия Геннадьевна Понятие логарифма
Понятие логарифма Кодирование факторов
Кодирование факторов Квадрат теңсіздіктер
Квадрат теңсіздіктер Занимательные размещения и перестановки
Занимательные размещения и перестановки Вписанная и описанная пирамиды. Домашнее задание
Вписанная и описанная пирамиды. Домашнее задание Определители матриц. Обратная матрица, ранг матрицы
Определители матриц. Обратная матрица, ранг матрицы Решение уравнений
Решение уравнений Первообразная. Неопределенный интеграл
Первообразная. Неопределенный интеграл Круглые тела. Цилиндр, конус, шар
Круглые тела. Цилиндр, конус, шар Мой класс в диаграммах и цифрах
Мой класс в диаграммах и цифрах Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Симплекс-метод
Симплекс-метод Длина окружности
Длина окружности Геометрия 11 класс
Геометрия 11 класс  5 класс.
5 класс.