Содержание
- 2. Элементы интегрального исчисления 1.Первообразная и неопределенный интеграл 2.Основные приемы вычисления неопределенных интегралов 3.Интегрирование функций, содержащих квадратный
- 3. Первообразная и неопределенный интеграл
- 4. Первообразная и неопределенный интеграл
- 5. Неопределенный интеграл Определение 1. Функция называется первообразной для в , если определена в и Пример.
- 6. Неопределенный интеграл Теорема (о разности первообразных). Доказательство. Обозначим через Пусть Функция удовлетворяет условиям теоремы Лагранжа: а)
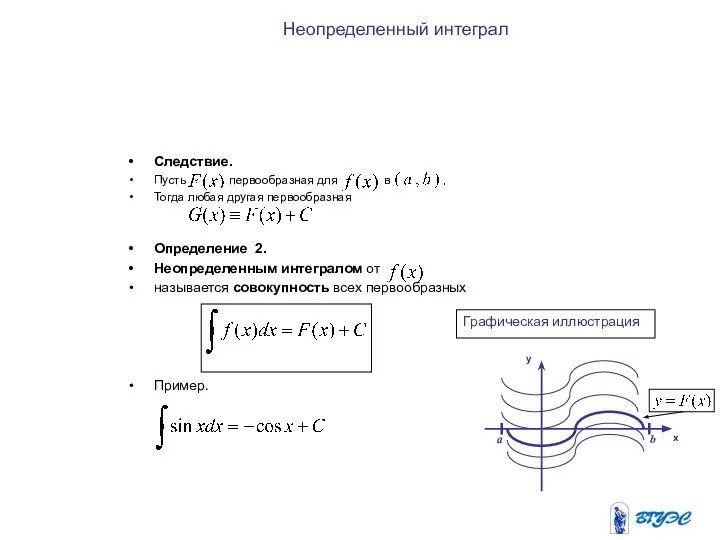
- 7. Неопределенный интеграл Следствие. Пусть первообразная для в . Тогда любая другая первообразная Определение 2. Неопределенным интегралом
- 8. Свойства интеграла, вытекающие из определения Производная неопределенного интеграла равна подынтегральной функции, а его дифференциал- подынтегральному выражению.
- 9. Свойства интеграла, вытекающие из определения Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции
- 10. Свойства интеграла
- 11. Таблица неопределенных интегралов
- 12. Таблица неопределенных интегралов
- 13. Интегрирование по частям
- 14. Метод замены переменной
- 15. Задача о вычислении площади плоской фигуры Решим задачу о вычислении площади фигуры, ограниченной графиком функции ,
- 16. Задача о вычислении площади плоской фигуры
- 17. Задача о вычислении площади плоской фигуры
- 18. Определенный интеграл
- 19. Определенный интеграл
- 20. Определенный интеграл
- 21. Теорема о существовании определенного интеграла
- 22. Свойства определенного интеграла
- 23. Свойства определенного интеграла
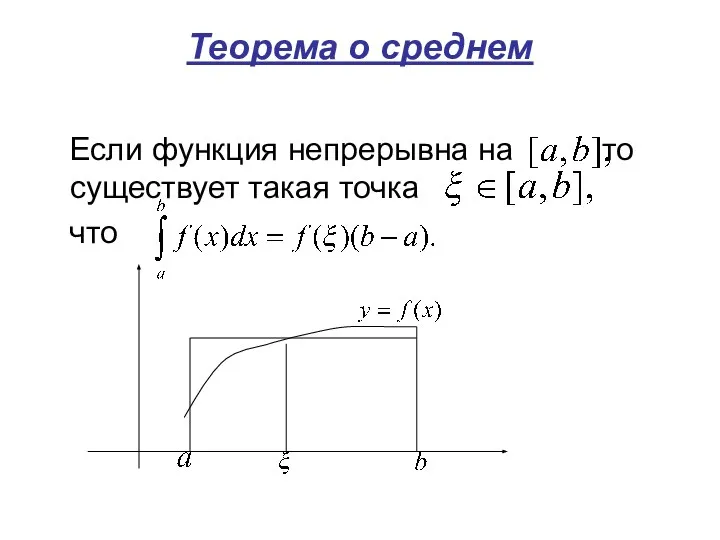
- 24. Теорема о среднем Если функция непрерывна на то существует такая точка что
- 25. Вычисление определенного интеграла
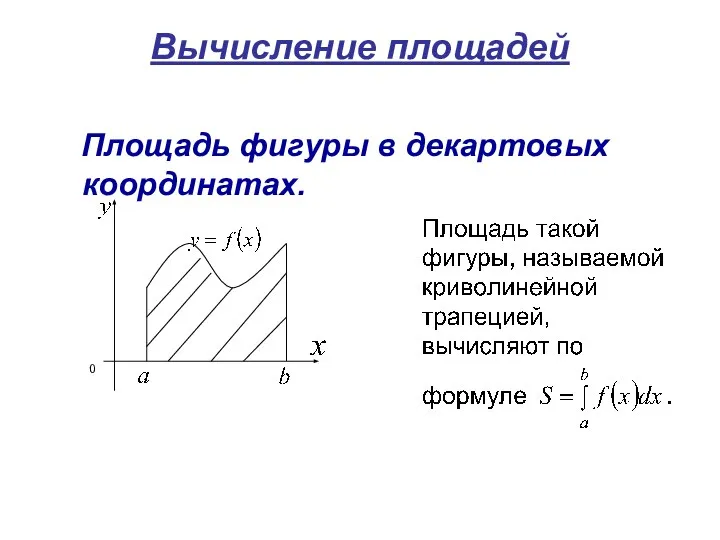
- 26. Вычисление площадей Площадь фигуры в декартовых координатах.
- 27. Обыкновенные дифференциальные уравнения
- 28. Уравнение первого порядка Функциональное уравнение F(x,y,y′) = 0 или y′= f(x,y), связывающее между собой независимую переменную,
- 29. Общее решение дифференциального уравнения 1-го порядка Общим решением дифференциального уравнения первого порядка называется такая функция y
- 30. Уравнение Ф(x,y,C) =0, определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения первого порядка.
- 31. Постановка задачи Коши Задача отыскания решения дифференциального уравнения , удовлетворяющего начальному условию при , называется задачей
- 32. Уравнение с разделяющимися переменными Дифференциальное уравнение называется уравнением с разделенными переменными.
- 33. Дифференциальное уравнение 1-го порядка называется уравнением с разделяющимися переменными, если оно имеет вид: . Для решения
- 34. Однородные уравнения Дифференциальное уравнение первого порядка называется однородным, если его можно привести к виду y′= или
- 35. Линейные уравнения 1-го порядка Дифференциальное уравнение первого порядка называется линейным, если оно содержит и в первой
- 36. Уравнение Бернулли Уравнением Бернулли называется уравнение 1-го порядка, имеющее вид , где и Его, как и
- 37. Основные понятия Уравнение 2-го порядка имеет вид Или Общим решением уравнения второго порядка называется такая функция
- 38. Задача Коши для уравнения 2-го порядка Если уравнение 2-го порядка разрешить относительно второй производной, то для
- 39. Теорема существования и единственности решения уравнения 2-го порядка Если в уравнении функция и ее частные производные
- 40. Уравнения 2-го порядка, допускающие понижение порядка Простейшее уравнение 2-го порядка решают двукратным интегрированием. Уравнение , не
- 41. Линейные однородные уравнения Линейным однородным дифференциальным уравнением второго порядка называется уравнение . Если все коэффициенты этого
- 42. Линейное однородное уравнение 2-го порядка с постоянными коэффициентами Уравнение называется характеристическим уравнением линейного уравнения . Оно
- 43. Вывод формул общего решения ЛОУ 2-го порядка Корни характеристического уравнения Случай 1. Если , то характеристическое
- 44. Случай 2. Если , то характеристическое уравнение имеет одинаковые корни . Частные решения ЛОУ выбираем так,
- 45. Случай 3. Если , то характеристическое уравнение имеет два комплексно-сопряженных корня и , где и .
- 47. Скачать презентацию









































 Тест по геометрии «Движение». 9 класс
Тест по геометрии «Движение». 9 класс Теория и практика решения задач по элементарной алгебре
Теория и практика решения задач по элементарной алгебре Обобщающий урок по теме «Четырехугольники»
Обобщающий урок по теме «Четырехугольники» Элементы статистической обработки данных
Элементы статистической обработки данных Статистические методы анализа данных параметров транспортного процесса
Статистические методы анализа данных параметров транспортного процесса Геометрический съезд (5 - 9 классы)
Геометрический съезд (5 - 9 классы) Урок геометрии 1 класс Выполнил учитель начальных классов МОУ Тунгусовской СОШ Петроченко М.П.
Урок геометрии 1 класс Выполнил учитель начальных классов МОУ Тунгусовской СОШ Петроченко М.П.  Теория графов
Теория графов Вневписанная окружность Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает
Вневписанная окружность Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает Столбчатые и круговые диаграммы
Столбчатые и круговые диаграммы Основные факты геометрии окружностей
Основные факты геометрии окружностей Десятки и единицы
Десятки и единицы Тригонометрические неравенства и методы их решения
Тригонометрические неравенства и методы их решения Математика « Гармония»2 класс Соотношение единиц длины.
Математика « Гармония»2 класс Соотношение единиц длины. Решение задач с величинами: цена, количество, стоимость
Решение задач с величинами: цена, количество, стоимость Пирамида
Пирамида Основы теории множеств
Основы теории множеств Вправи й задачі на засвоєння таблиць додавання і віднімання числа 7. Розпізнавання геометричних фігур
Вправи й задачі на засвоєння таблиць додавання і віднімання числа 7. Розпізнавання геометричних фігур Теорема Виета
Теорема Виета Цифры от 0 до 9. УМК «Планета знаний»
Цифры от 0 до 9. УМК «Планета знаний» Открытый интенсив по математике. Самое важное. День 3
Открытый интенсив по математике. Самое важное. День 3 Применение производной к исследованию функций 2 курс
Применение производной к исследованию функций 2 курс Аттестационная работа. Математические задачи о г. Химки
Аттестационная работа. Математические задачи о г. Химки Урок «Морское путешествие» по теме «Прибавление числа 2. Закрепление пройденного» Цель: работа над числовым рядом; повторение сос
Урок «Морское путешествие» по теме «Прибавление числа 2. Закрепление пройденного» Цель: работа над числовым рядом; повторение сос Статистика. Загальні поняття про статистику
Статистика. Загальні поняття про статистику Квадратные корни. Обобщающий урок
Квадратные корни. Обобщающий урок Сравнение двух средних нормальных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки)
Сравнение двух средних нормальных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки) Теорема Пифагора
Теорема Пифагора