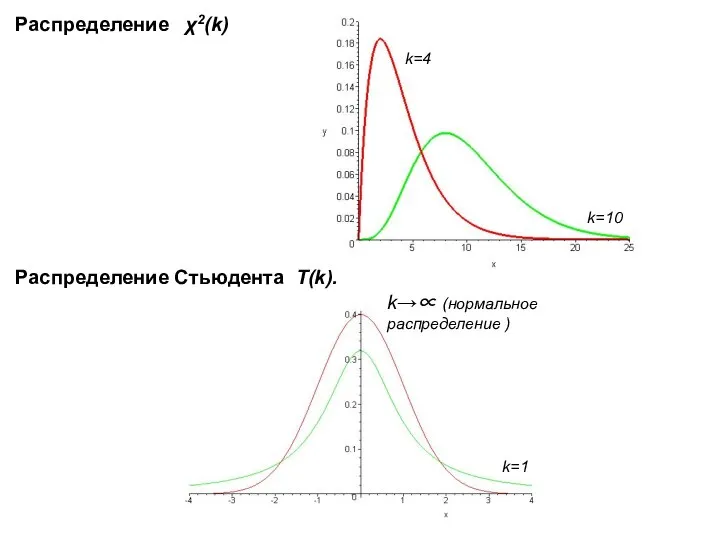
Распределение χ2
Пусть Xi(i=1,2,..,n)- независимые случайные величины ,каждая из которых имеет распределение
N(0,1). Тогда сумма квадратов этих величин распределена по закону χ2 («хи-квадрат») с n степенями свободы.
Распределение Стьюдента
Пусть Z независимая нормально распределенная случайная величина , N(0,1). V- независимая от Z случайная величина, которая распределена по закону χ2 с n степенями свободы. Тогда величина имеет распределение Стьюдента с n степенями свободы.
(Стьюдент псевдоним английского статистика В. Госсета)
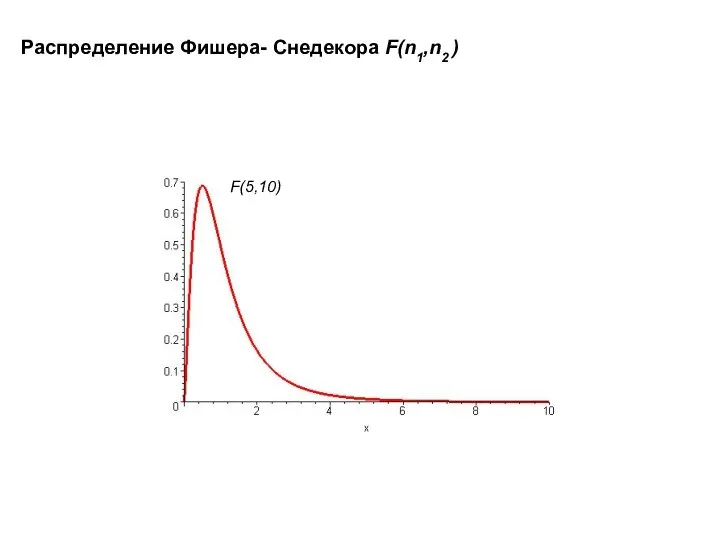
Распределение Фишера- Снедекора
Пусть U и V независимые случайные величины, распределенные по закону χ2 со степенями свободы k1 и k2, то величина имеет распределение F Фишера- Снедекора со степенями свободы k1 и k2 .











 Сочетания и их свойства. 9 класс
Сочетания и их свойства. 9 класс Фракталы Проект выполнила Маницына Анастасия
Фракталы Проект выполнила Маницына Анастасия Работа с одной выборкой. Парные сравнения
Работа с одной выборкой. Парные сравнения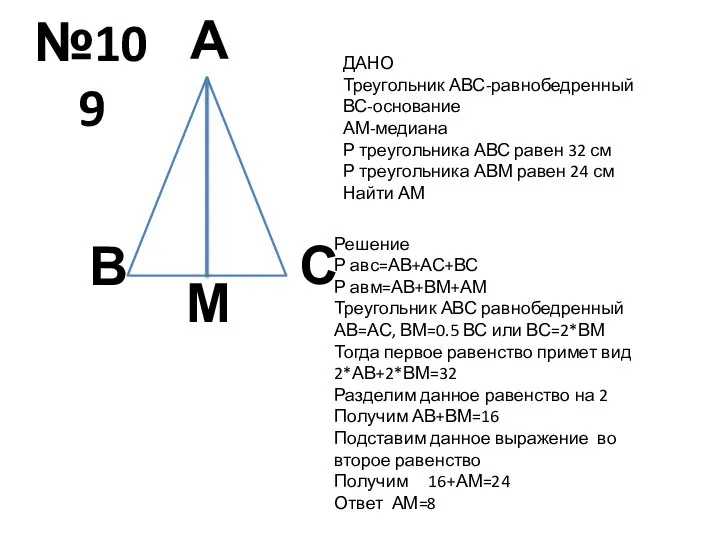 Равнобедренный треугольник. Задача
Равнобедренный треугольник. Задача Средняя линия треугольника
Средняя линия треугольника Построение графика функции Y = F(X+L) + M
Построение графика функции Y = F(X+L) + M Тождественные преобразования тригонометрических выражений
Тождественные преобразования тригонометрических выражений Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Дискретная математика. Основные понятия теории множеств. (Лекция 1.1)
Дискретная математика. Основные понятия теории множеств. (Лекция 1.1) Презентация на тему ЧЕТЫРЕХЗНАЧНЫЕ ЧИСЛА
Презентация на тему ЧЕТЫРЕХЗНАЧНЫЕ ЧИСЛА Геометрия Лобачевского
Геометрия Лобачевского Кубик Рубика и математика
Кубик Рубика и математика Задачи с величинами. Цена, количество, стоимость (2 класс)
Задачи с величинами. Цена, количество, стоимость (2 класс) Функции, предназначенные для работы над списками
Функции, предназначенные для работы над списками Аттестационная работа. Применение математических методов в исследовании арт-рынка
Аттестационная работа. Применение математических методов в исследовании арт-рынка Сумма бесконечной геометрической прогрессии. Устная работа
Сумма бесконечной геометрической прогрессии. Устная работа Вопросы Что такое модель? Приведи пример материальных моделей. Приведи пример информационных моделей. Перечили цели создания мо
Вопросы Что такое модель? Приведи пример материальных моделей. Приведи пример информационных моделей. Перечили цели создания мо Основы функционального анализа. Глава 2. Линейные нормированные пространства
Основы функционального анализа. Глава 2. Линейные нормированные пространства Логарифмические уравнения
Логарифмические уравнения Повторение по теме «треугольник». 9 класс
Повторение по теме «треугольник». 9 класс Графы. Основные определения, способы задания
Графы. Основные определения, способы задания Признаки равенства треугольников
Признаки равенства треугольников Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Бір факторлы және екі факторлы дисперсиялық талдау
Бір факторлы және екі факторлы дисперсиялық талдау Использование нетрадиционных методов при подготовке к ЕГЭ по математике
Использование нетрадиционных методов при подготовке к ЕГЭ по математике Решение задач на движение
Решение задач на движение Построение сечений
Построение сечений Дробные выражения
Дробные выражения