Содержание
- 3. 4) Интегрируют каждую простейшую дробь.
- 4. Правильную рациональную дробь можно разложить на сумму простейших дробей четырех типов:
- 5. Коэффициенты Ai,Mi,Ni могут быть найдены после приведения суммы простейших дробей к общему знаменателю.
- 6. Пример. Разлагаем правильную дробь на сумму простейших дробей:
- 8. По свойству линейности:
- 9. Интегрирование выражений, содержащих тригонометрические функции. а) n и m – чётные, целые, положительные. Метод: понижение степени
- 11. Пример. Решение.
- 12. б) хотя бы одно из n и m - нечётное, целое, положительное. Метод:от нечётной степени отделяется
- 13. Пример 1: Решение.
- 14. Пример 2: Решение.
- 15. Метод: переход к сумме функций и сумме интегралов. При этом используются следующие тригонометрические формулы:
- 17. Метод - универсальная тригонометрическая подстановка: рациональная функция. Здесь
- 20. Окончательно: (Интеграл приводится к интегралу от рациональной дроби).
- 21. Пример. Решение.
- 22. Замечание. Если подынтегральная функция R(sinx,cosx) является чётной функцией аргументов sinx и cosx, более эффективной будет подстановка
- 24. Скачать презентацию





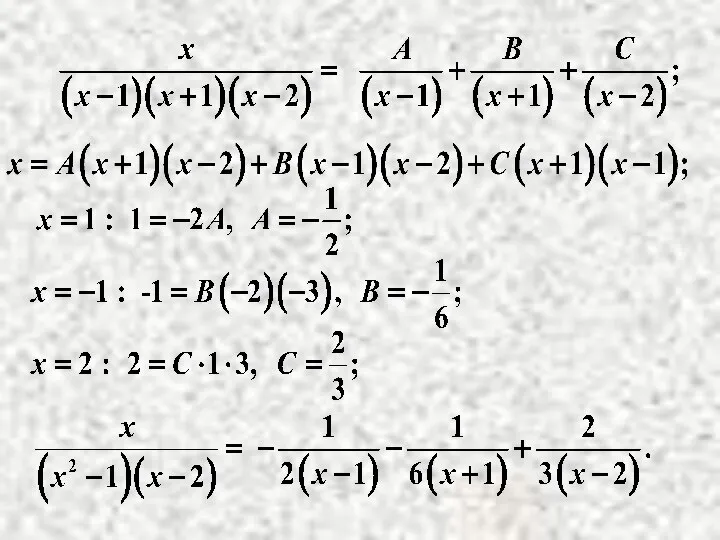
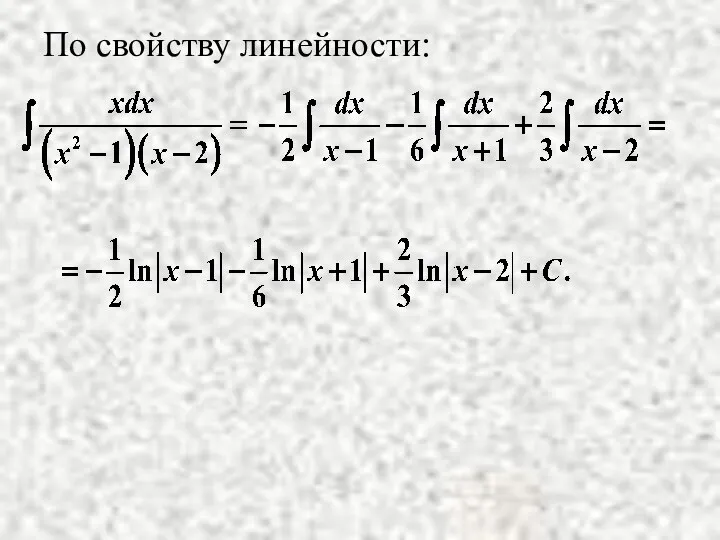

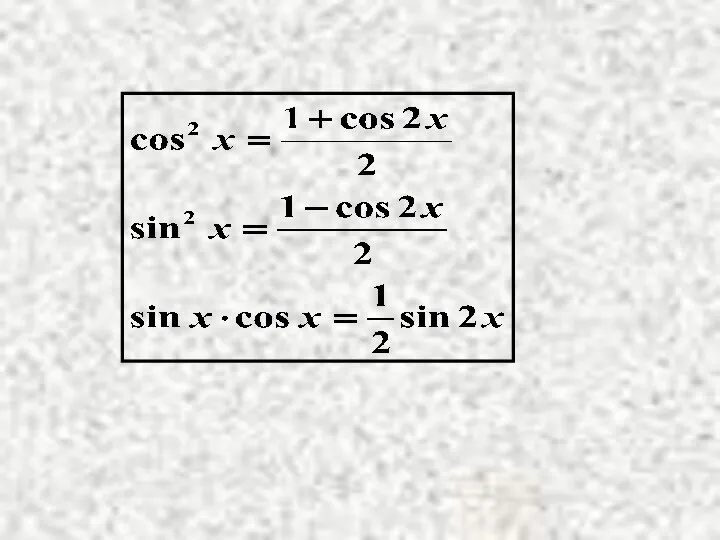
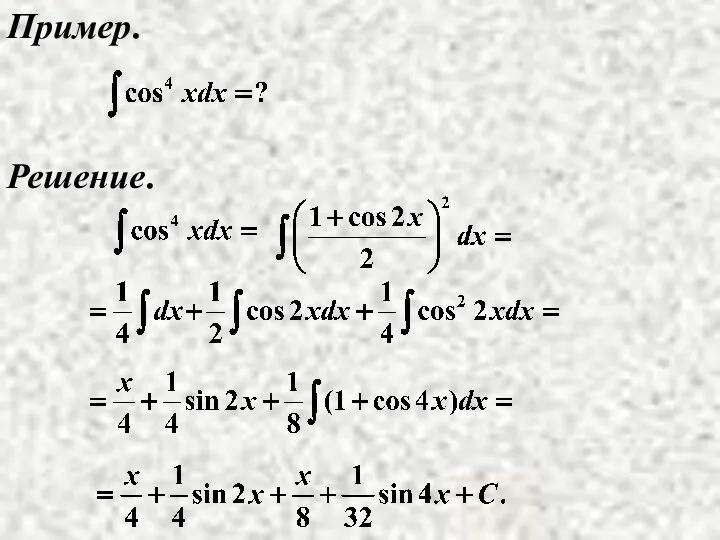

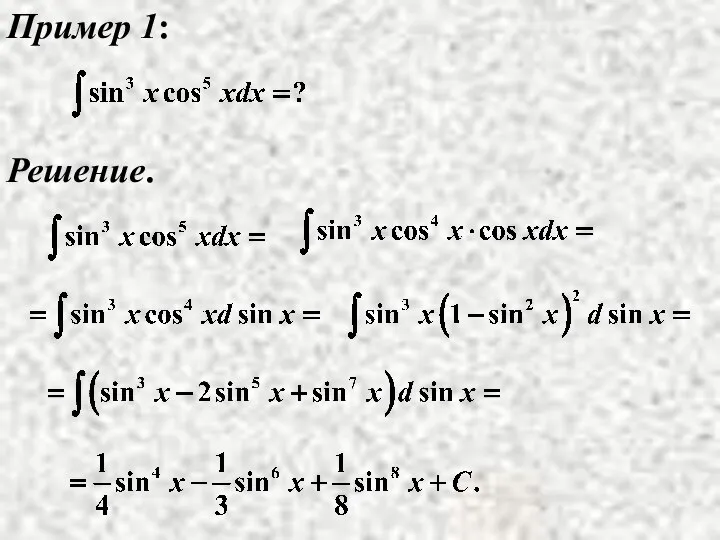
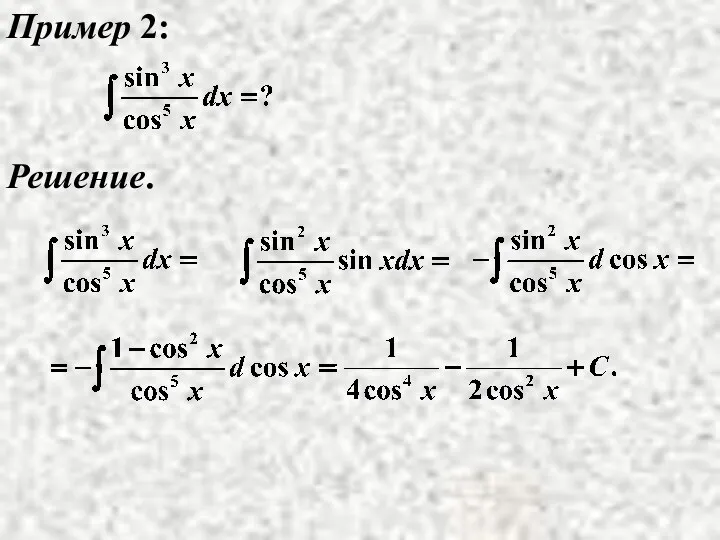

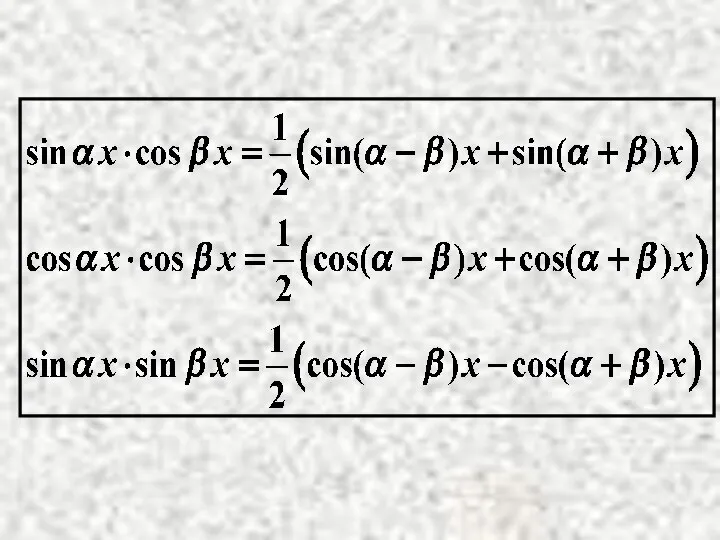

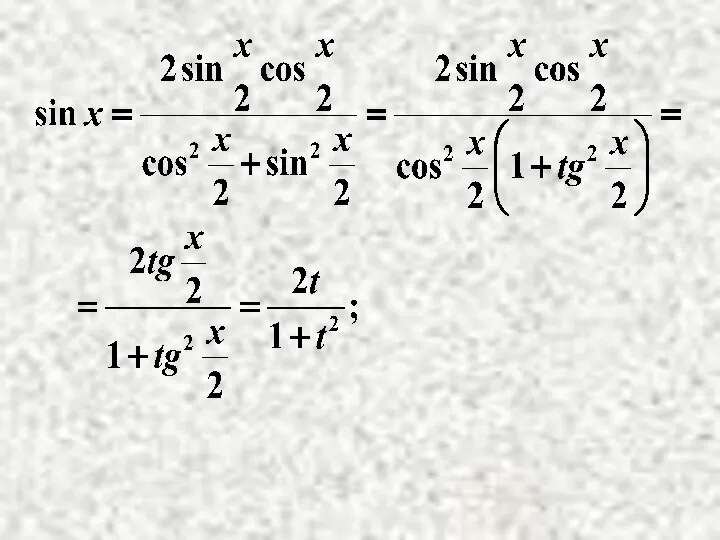
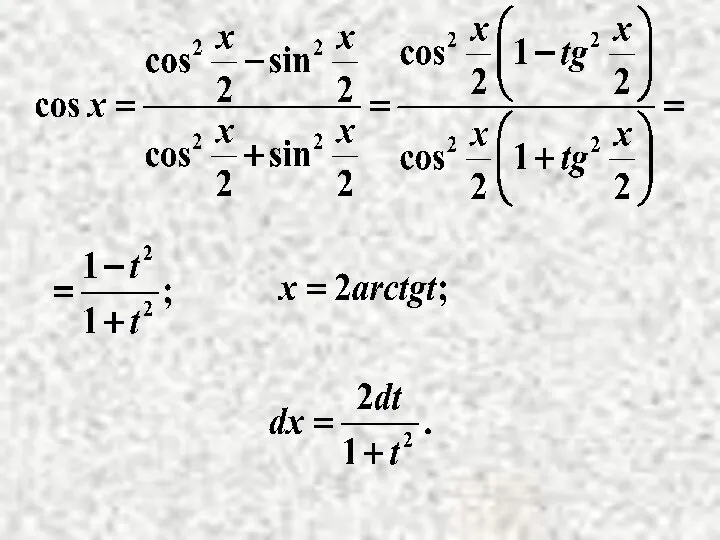

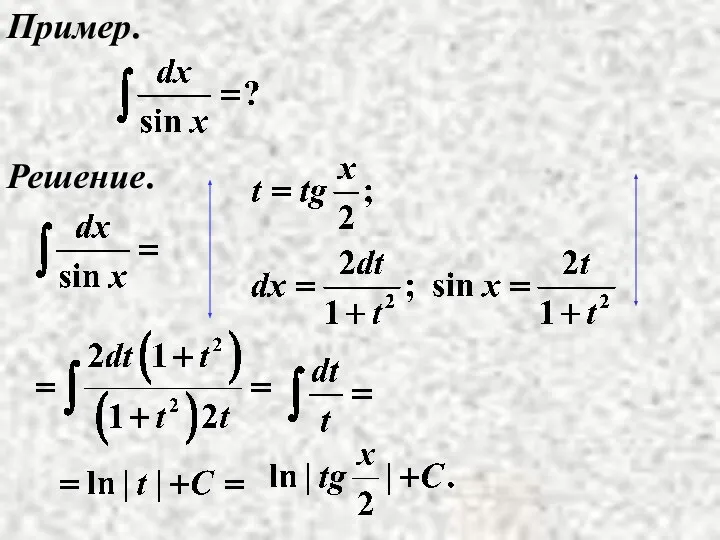

 Угол. Прямой и развернутый угол. Чертежный треугольник
Угол. Прямой и развернутый угол. Чертежный треугольник Цилиндр. Задачи
Цилиндр. Задачи Степенная функция
Степенная функция Введение в методологию CFD
Введение в методологию CFD Решение задач на нахождение площади фигур 6 класс 2006-07 уч.г.
Решение задач на нахождение площади фигур 6 класс 2006-07 уч.г.  Гипотенуза и катеты в треугольнике. Задачи
Гипотенуза и катеты в треугольнике. Задачи Урок математики во 2 классе
Урок математики во 2 классе  Лекция 7. Приложения производной. Дифференциал функции
Лекция 7. Приложения производной. Дифференциал функции Геометрические фигуры
Геометрические фигуры Формулы сокращенного умножения. 7 класс
Формулы сокращенного умножения. 7 класс Способы решения уравнения sinX - cosX = 1
Способы решения уравнения sinX - cosX = 1 Введение и история появления бустинга
Введение и история появления бустинга Теоремы сложения и умножения вероятностей
Теоремы сложения и умножения вероятностей Математический тренажер для 1 класса. Тема: Сложение и вычитание в пределах 10
Математический тренажер для 1 класса. Тема: Сложение и вычитание в пределах 10 Множества. Основные понятия
Множества. Основные понятия Метр. (2класс)
Метр. (2класс) Изображение объемана на плоскости и линейная перспектива
Изображение объемана на плоскости и линейная перспектива Решение задач по теме «Подобные слагаемые»
Решение задач по теме «Подобные слагаемые» Задачи на проценты
Задачи на проценты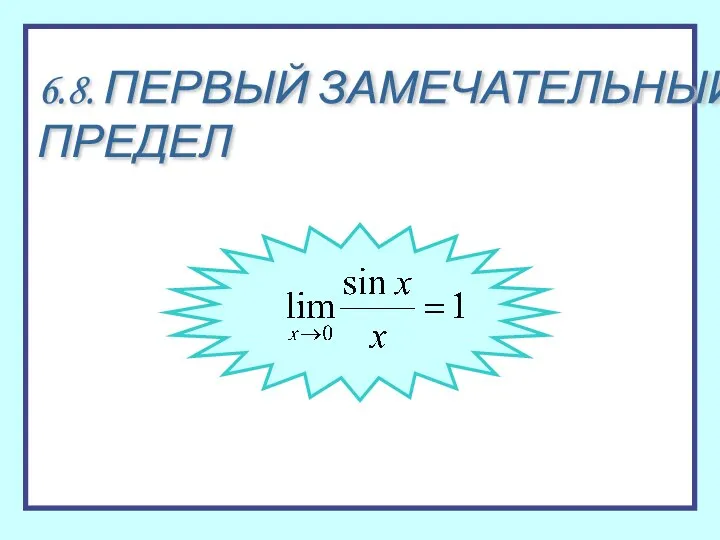 Первый замечательный предел
Первый замечательный предел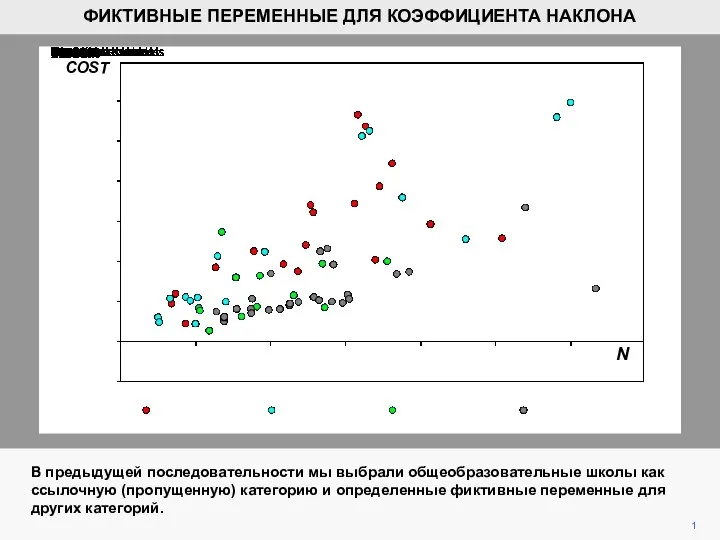 Фиктивные переменные для коэффициента наклона
Фиктивные переменные для коэффициента наклона Степень числа. Квадрат и куб числа. 5 класс
Степень числа. Квадрат и куб числа. 5 класс Множества. Понятие множества
Множества. Понятие множества Функция y = sin x, ее свойства и график
Функция y = sin x, ее свойства и график Подготовка к контрольной работе №3. Тема: Корреляционный и регрессионный анализ
Подготовка к контрольной работе №3. Тема: Корреляционный и регрессионный анализ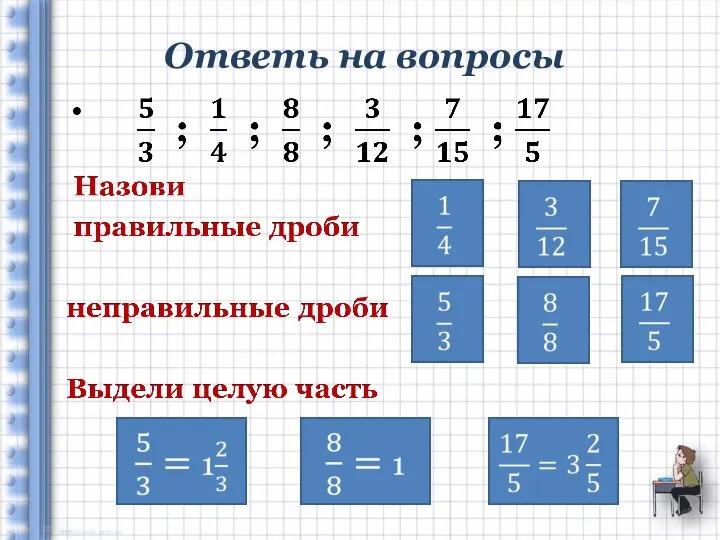 Ответь на вопросы. 5 класс
Ответь на вопросы. 5 класс Деление с остатком
Деление с остатком Координаты вектора
Координаты вектора