Содержание
- 2. ПЛАН: Основные понятия. Формы записи. Действия над комплексными числами: Сложение комплексных чисел; Вычитание комплексных чисел; Умножение
- 3. Основные понятия. Определение. Комплексным числом Ζ называется выражение вида , где α и β- действительные числа,
- 4. Основные понятия. Два комплексных числа называются равными тогда и только тогда, когда равны их действительные и
- 5. Примеры. Пример 1. Пример 2.
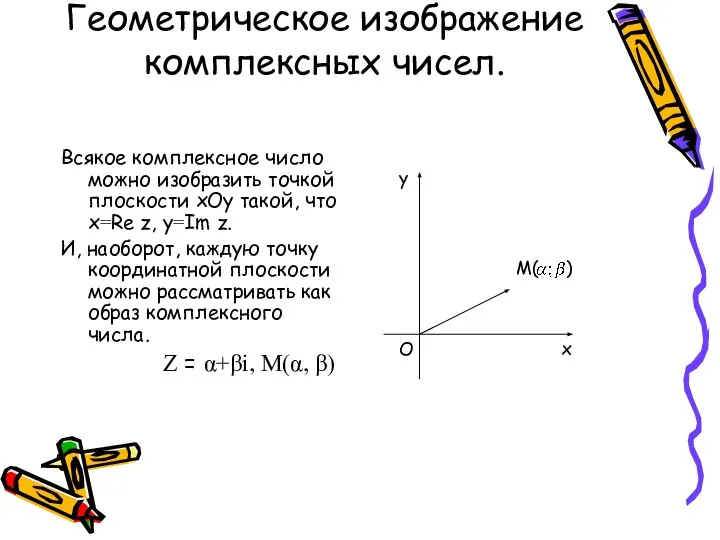
- 6. Геометрическое изображение комплексных чисел. Всякое комплексное число можно изобразить точкой плоскости xOy такой, что x=Re z,
- 7. Геометрическое изображение комплексных чисел. Плоскость, на которой изображается комплексные числа, называется комплексной плоскостью. Ось абсцисс Ox
- 8. Геометрическое изображение комплексных чисел. Комплексное число можно задавать с помощью радиус-вектора . Длина вектора называется модулем
- 9. Формы записи комплексных чисел. Алгебраическая. Тригонометрическая. Показательная. Любое комплексное число можно записать в любой форме.
- 10. Формы записи комплексных чисел. Запись числa z=α+βi называется алгебраической формой комплексного числа. Запись числа z в
- 11. Переход от одной формы к другой. От алгебраической формы к тригонометрической Т.к. То От тригонометрической формы
- 12. При переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить главное значение аргумента, т.е. Т.к.
- 13. Пример: Комплексное число изобразить на плоскости и записать в тригонометрической форме 2 2 φ x y
- 14. Комплексное число можно записать в показательной (или экспонентной) форме Где и В силу формулы Эйлера функция
- 15. 2. Действия над комплексными числами Суммой двух комплексных чисел Называется комплексное число Разностью двух комплексных чисел
- 16. Сложение (вычитание) комплексных чисел Примеры: 1. 2.
- 17. Произведение и частное комплексных чисел в алгебраической форме. Произведением двух комплексных чисел называется комплексное число Формула
- 18. Произведение и частное комплексных чисел в алгебраической форме. Произведение: Частное:
- 19. Произведение и частное комплексных чисел в тригонометрической форме. Произведение чисел Находим по формуле При умножении модули
- 20. Произведение и частное комплексных чисел в тригонометрической форме. Произведение: Частное:
- 21. Произведение и частное комплексных чисел в показательной форме.
- 22. Возведение комплексных чисел в степень. Правило умножения комплексных чисел позволяет возвести число в n-степень: Получим Формулу
- 23. Возведение комплексных чисел в степень. Пример. Найти Запишем число в тригонометрической форме:
- 24. Извлечение корней из комплексных чисел в тригонометрической форме. Определение. Корнем n-й степени из комплексного числа z
- 26. Скачать презентацию






















 Начертательная геометрия. Точка и линия на поверхности. Коноид. Тело вращения. Геликоид
Начертательная геометрия. Точка и линия на поверхности. Коноид. Тело вращения. Геликоид Уроки математики с любимыми героями. Простые множители
Уроки математики с любимыми героями. Простые множители Презентация по математике "Решение планиметрических задач на нахождение углов геометрических фигур" - скачать бесплатно
Презентация по математике "Решение планиметрических задач на нахождение углов геометрических фигур" - скачать бесплатно Правильные многоугольники
Правильные многоугольники Углы, связанные с окружностью. Устные задания
Углы, связанные с окружностью. Устные задания Длина окружности
Длина окружности Нестандартные задачи как средство формирования исследовательских умений обучающихся в курсе алгебры 8 класса
Нестандартные задачи как средство формирования исследовательских умений обучающихся в курсе алгебры 8 класса Смежные углы. Карточки для работы в паре
Смежные углы. Карточки для работы в паре Избранные лекции по математическому анализу
Избранные лекции по математическому анализу Простейший многоугольник - треугольник
Простейший многоугольник - треугольник « Использование системно-деятельностнoго подхода на уроках математики»
« Использование системно-деятельностнoго подхода на уроках математики» Поле чудес. Геометрия 9 класс
Поле чудес. Геометрия 9 класс Історія виникнення дробів
Історія виникнення дробів Тренажёр «Дартс». Умножение
Тренажёр «Дартс». Умножение Функція f(x)=sin x
Функція f(x)=sin x Решение задач на деление дробей
Решение задач на деление дробей Вычитание смешанных дробей
Вычитание смешанных дробей Эффективные методы решения неравенств с одной переменной (типовые задания С3)
Эффективные методы решения неравенств с одной переменной (типовые задания С3)  Презентация по математике "Учимся считать от 0 до 10" - скачать
Презентация по математике "Учимся считать от 0 до 10" - скачать  Расчет центральной предельной теоремы
Расчет центральной предельной теоремы Презентация по математике "Числовые и буквенные выражения" - скачать
Презентация по математике "Числовые и буквенные выражения" - скачать  Построение параллельных прямых
Построение параллельных прямых Математика для начальных классов
Математика для начальных классов Случайные процессы (лекция 14). Каноническое разложение случайных процессов
Случайные процессы (лекция 14). Каноническое разложение случайных процессов Презентация на тему Математика в моей семье
Презентация на тему Математика в моей семье  Движение_в_противоположном_направлении
Движение_в_противоположном_направлении Математическое моделирование
Математическое моделирование Округление чисел. Цели: повторить изученную тему, подготовиться к контрольной работе. Подготовила учитель математики МБОУ СОШ №1
Округление чисел. Цели: повторить изученную тему, подготовиться к контрольной работе. Подготовила учитель математики МБОУ СОШ №1