Содержание
- 2. §10. Криволинейный интеграл II рода (по координатам) 1. Задача, приводящая к криволинейному интегралу II рода Пусть
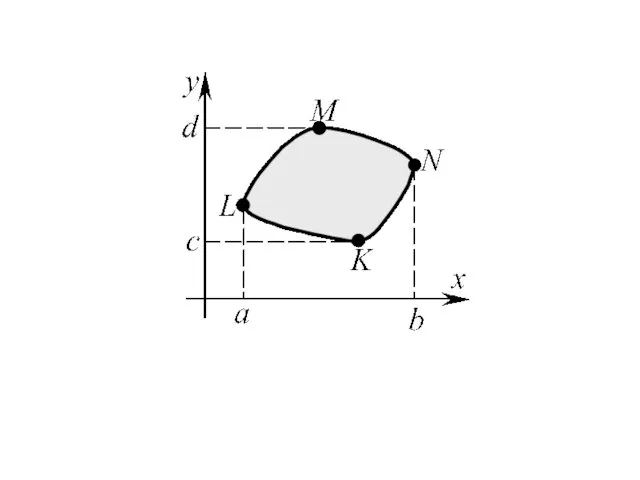
- 3. 2. Определение и свойства криволинейного интеграла II рода Пусть (ℓ) = (L1L2) – простая (т.е. без
- 4. Пусть Число I называется пределом интегральных сумм In(Mi , Ki) при λ → 0 , если
- 5. Аналогично определяются интегралы Сумму записывают в виде и называют криволинейным интегралом II рода (по координатам).
- 6. СВОЙСТВА КРИВОЛИНЕЙНОГО ИНТЕГРАЛА II РОДА Замечание: предполагаем, что все рассматриваемые в свойствах интегралы существуют. 1. Криволинейный
- 7. На плоскости положительным направлением обхода является направление против хода часовой стрелки. Криволинейный интеграл II рода по
- 8. 4. Постоянный множитель можно выносить за знак криволиней- ного интеграла II рода, т.е. 3. ФИЗИЧЕСКИЙ СМЫСЛ
- 9. 5. Криволинейный интеграл II рода от алгебраической суммы двух (конечного числа) функций равен алгебраической сумме криволинейных
- 10. 3. Вычисление криволинейного интеграла II рода Пусть простая (не имеющая кратных точек) кривая (ℓ)=(L1L2) задана параметрическими
- 11. СЛЕДСТВИЕ 2. Если выполнены условия: 1) (ℓ) = (L1L2) – гладкая кривая в плоскости xOy ,
- 12. 4. Связь между криволинейными интегралами II рода и двойными интегралами Пусть (σ) – замкнутая ограниченная область
- 14. 5. Криволинейные интегралы II рода, не зависящие от пути интегрирования ЛЕММА 4. Для того, чтобы криволинейный
- 15. ТЕОРЕМА 5. Пусть функции P(x,y,z), Q(x,y,z), R(x,y,z) непре- рывны вместе со своими частными производными в некото-
- 16. 6. Интегрирование полных дифференциалов Пусть Pdx + Qdy + Rdz = du ; (ℓ) = (L1L2)
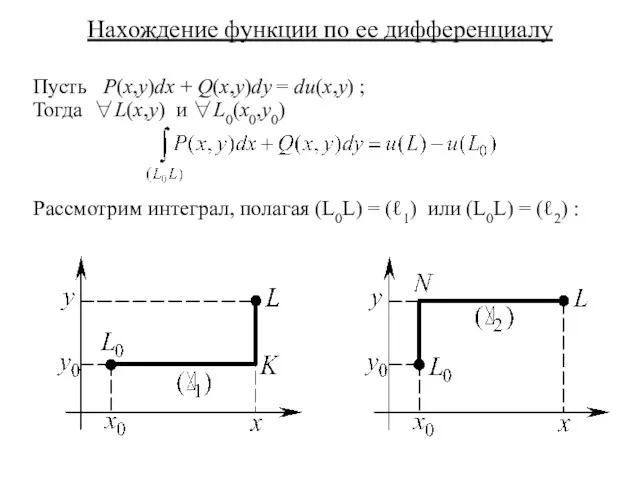
- 17. Нахождение функции по ее дифференциалу Пусть P(x,y)dx + Q(x,y)dy = du(x,y) ; Тогда ∀L(x,y) и ∀L0(x0,y0)
- 18. Получили: или 7. Связь криволинейных интегралов I и II рода Если (ℓ) – простая гладкая кривая,
- 20. Скачать презентацию















 Рабочая программа по математике для 5 класса по УМК И.И. Зубаревой и А.Г. Мордковича Подготовила Олейник Р.Б. 2014год
Рабочая программа по математике для 5 класса по УМК И.И. Зубаревой и А.Г. Мордковича Подготовила Олейник Р.Б. 2014год Сечение куба и сечение тетраэдра
Сечение куба и сечение тетраэдра Алгоритм решения квадратных неравенств
Алгоритм решения квадратных неравенств Математическая логика
Математическая логика Анализ временных рядов
Анализ временных рядов Формулы приведения
Формулы приведения Линейное пространство. Базис. Линейная оболочка (УСР). Лекция 17
Линейное пространство. Базис. Линейная оболочка (УСР). Лекция 17 Десятичные дроби
Десятичные дроби Бином Ньютона. Полиномиальная формула. (Лекция 11)
Бином Ньютона. Полиномиальная формула. (Лекция 11) Пропорция и проценты
Пропорция и проценты Деление одночленов
Деление одночленов Властивості предметів. Порівняння чисел і предметів. Знаки <, >, =
Властивості предметів. Порівняння чисел і предметів. Знаки <, >, = Применение производной к исследованию функций
Применение производной к исследованию функций Квадрат
Квадрат Тангенс и котангенс
Тангенс и котангенс Аналитическая геометрия
Аналитическая геометрия Крупное научное открытие дает решение крупной проблемы, но в решении любой задачи присутствует крупица открытия .
Крупное научное открытие дает решение крупной проблемы, но в решении любой задачи присутствует крупица открытия .  Динамика нелинейного тентообразного отображения с параметром
Динамика нелинейного тентообразного отображения с параметром Введение в математическую логику и теорию алгоритмов
Введение в математическую логику и теорию алгоритмов В мире песочных форм и фигур
В мире песочных форм и фигур Проект "Математика вокруг нас". Узоры на посуде. (2 класс)
Проект "Математика вокруг нас". Узоры на посуде. (2 класс) Отмеривание отрезка заданной длины
Отмеривание отрезка заданной длины Решение линейных уравнений. 7класс Автор: Богданова Н.Ю., учитель математики МОУ СОШ №7, г.Губкинский, ЯНАО.
Решение линейных уравнений. 7класс Автор: Богданова Н.Ю., учитель математики МОУ СОШ №7, г.Губкинский, ЯНАО.  Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Формулы сокращённого умножения. Урок обобщения знаний
Формулы сокращённого умножения. Урок обобщения знаний Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Дискретные структуры. Теория множеств. Cоответствия. Функции. Отображения
Дискретные структуры. Теория множеств. Cоответствия. Функции. Отображения Логарифмические уравнения
Логарифмические уравнения