Содержание
- 2. Квадратичной функцией называется функция, заданная формулой у = ах2 + bх + с, а ≠ 0.
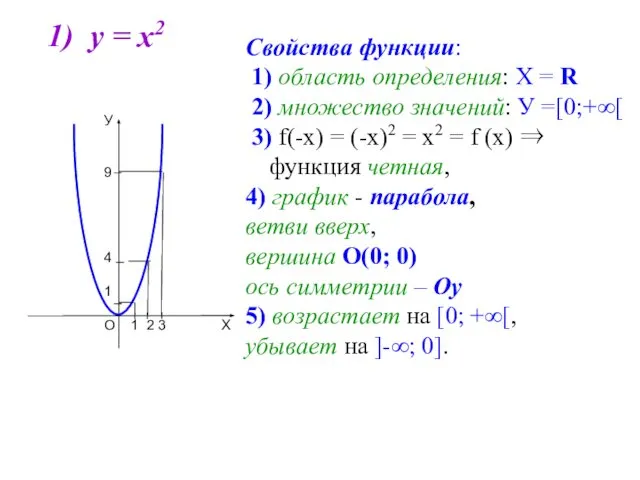
- 3. 1) у = х2 Свойства функции: 1) область определения: Х = R 2) множество значений: У
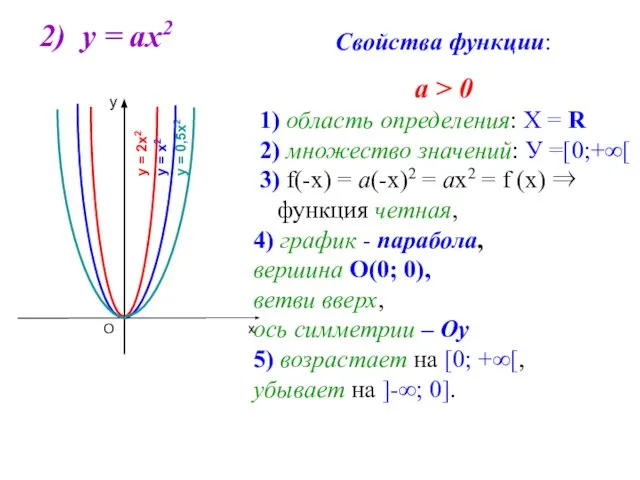
- 4. 2) у = ах2 Свойства функции: а > 0 1) область определения: Х = R 2)
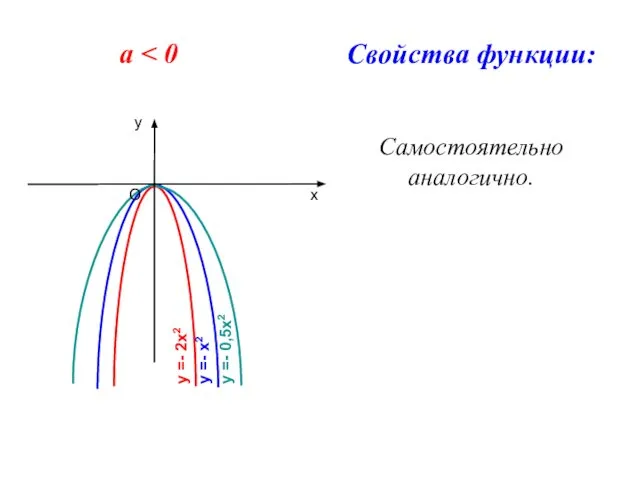
- 5. а Свойства функции: Самостоятельно аналогично.
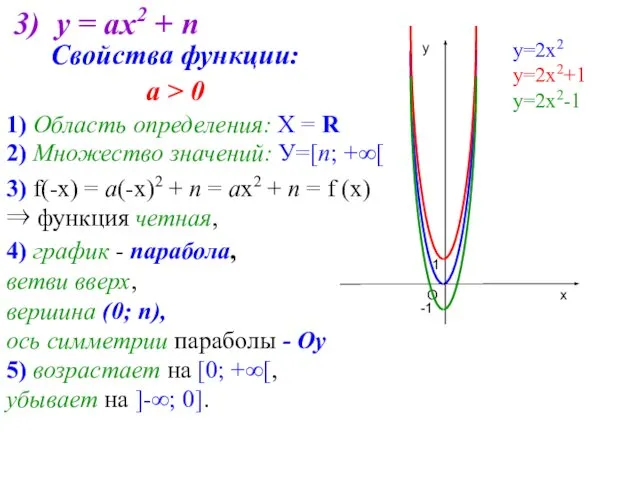
- 6. 3) у = ах2 + n 3) f(-х) = а(-х)2 + n = ах2 + n
- 7. Свойства функции: а Самостоятельно аналогично
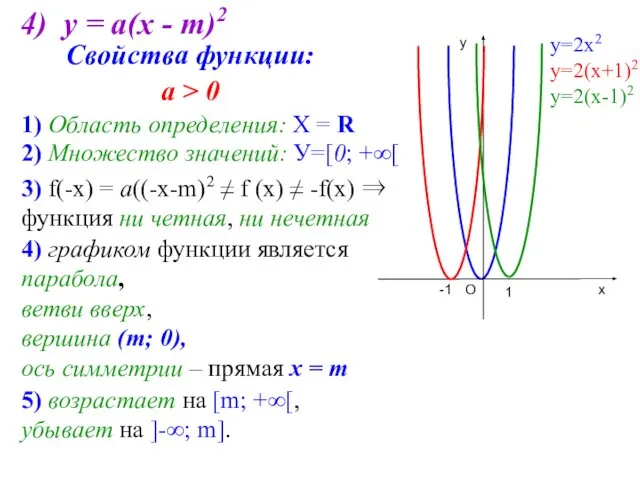
- 8. 4) у = а(х - m)2 3) f(-х) = а((-х-m)2 ≠ f (х) ≠ -f(х) ⇒
- 9. Свойства функции: а Самостоятельно аналогично
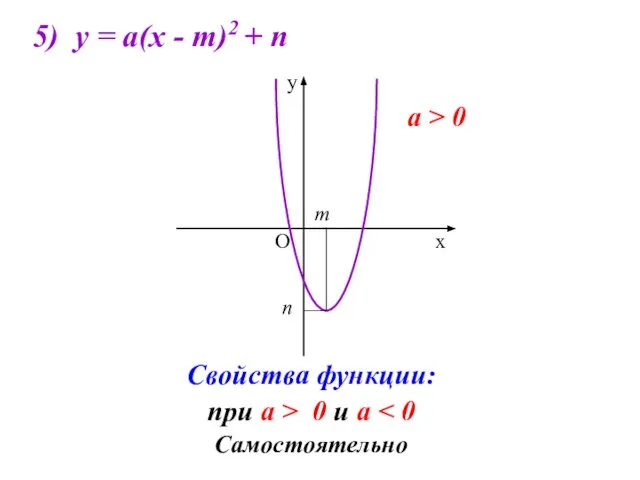
- 10. 5) у = а(х - m)2 + n Свойства функции: при а > 0 и а
- 11. Построение графика функции у = ах2 + bх + с 1 способ из квадратного трехчлена ах2
- 12. 2) определить координаты вершины параболы – (m; n) 3) построить вспомогательный график функции у = ах2
- 13. 2 способ 1) Найти координаты вершины параболы: абсцисса , ордината у0 = у(х0) 2) Найти (если
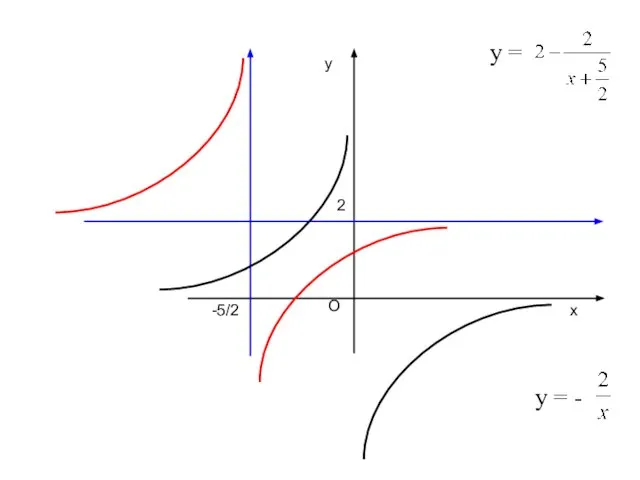
- 14. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ Дробно-линейной функцией называется функция у = , полученная при делении друг на друга двух
- 15. 3) с ≠ 0, d ≠ 0, аd = bс ⇒ = р ⇒ а =
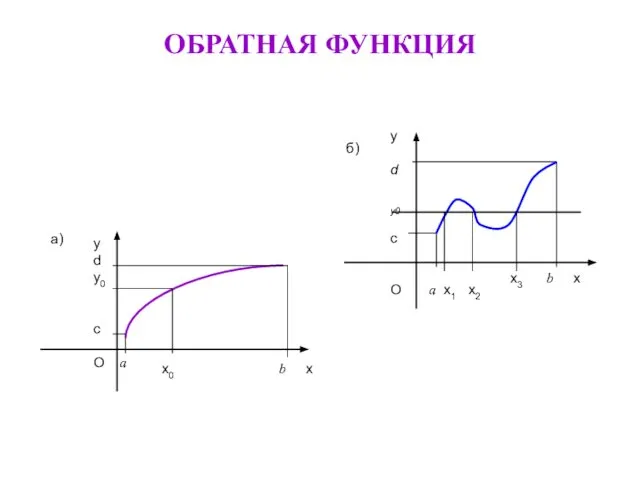
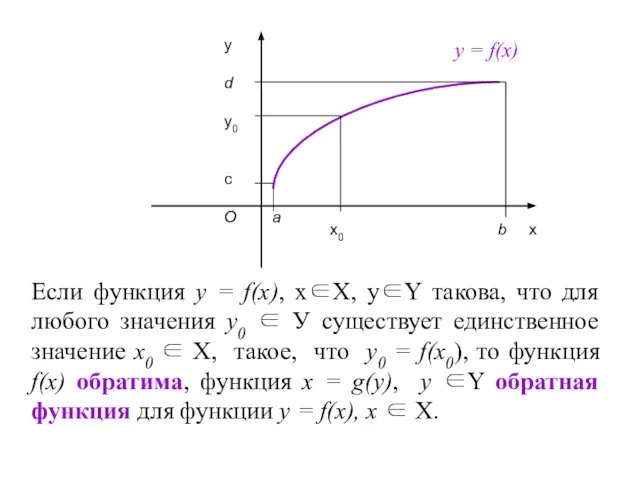
- 17. ОБРАТНАЯ ФУНКЦИЯ
- 18. Если функция у = f(х), х∈Х, у∈Y такова, что для любого значения у0 ∈ У существует
- 19. Чтобы найти выражение для обратной функции, надо решить уравнение у = f(х) относительно х, беря лишь
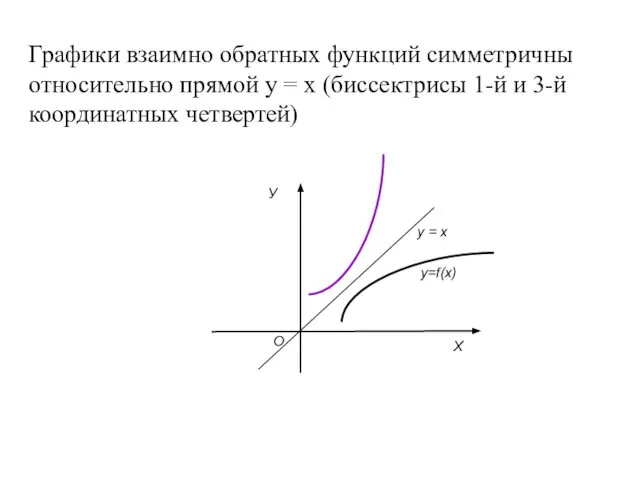
- 20. Графики взаимно обратных функций симметричны относительно прямой у = х (биссектрисы 1-й и 3-й координатных четвертей)
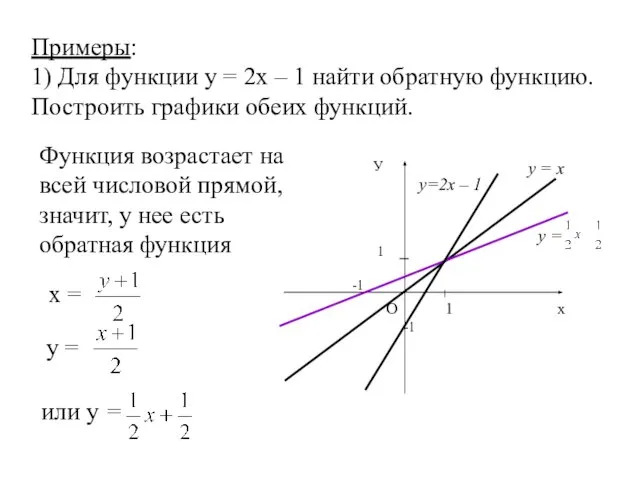
- 21. Примеры: 1) Для функции у = 2х – 1 найти обратную функцию. Построить графики обеих функций.
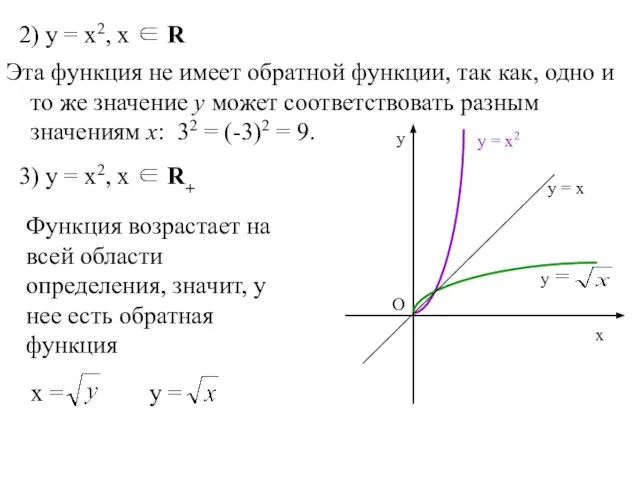
- 22. 2) у = х2, х ∈ R Эта функция не имеет обратной функции, так как, одно
- 23. КОМПОЗИЦИЯ ФУНКЦИЙ у = f(х), х ∈ Х и х = g(t), t ∈ Т, х
- 24. Примеры: 1) у = х2 + 1 и х = 3t – 4, у(х(t))= (3t –
- 26. Скачать презентацию











 Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Тождественные преобразования
Тождественные преобразования «Путешествие на поезде»
«Путешествие на поезде» ЕГЭ. Профильная математика. № 3
ЕГЭ. Профильная математика. № 3 Алгоритм сложения двузначных чисел
Алгоритм сложения двузначных чисел Весёлая математика. (ДОУ)
Весёлая математика. (ДОУ) Влияние коэффициентов а, b и с на расположение графика квадратичной функции. 9 класс
Влияние коэффициентов а, b и с на расположение графика квадратичной функции. 9 класс Введение в теорию систем
Введение в теорию систем Математический диктант
Математический диктант Предел функции
Предел функции Координатная плоскость
Координатная плоскость Сложения и вычитания в пределах 10 (по мотивам русской народной сказки Колобок)
Сложения и вычитания в пределах 10 (по мотивам русской народной сказки Колобок) Параллельное проектирование
Параллельное проектирование Презентация на тему Тригонометрия
Презентация на тему Тригонометрия  Решение задач линейного программирования симплекс-методом. Двойственность ЗЛП
Решение задач линейного программирования симплекс-методом. Двойственность ЗЛП Применение теоремы Пифагора
Применение теоремы Пифагора Методы решения показательных уравнений
Методы решения показательных уравнений Временные ряды и их предварительный анализ
Временные ряды и их предварительный анализ Координаты на прямой
Координаты на прямой Параллельное проектирование
Параллельное проектирование Презентация по математике "ПРИНЦИПЫ СИСТЕМНОГО АНАЛИЗА" - скачать
Презентация по математике "ПРИНЦИПЫ СИСТЕМНОГО АНАЛИЗА" - скачать  Кто где живет? Головоломки
Кто где живет? Головоломки Проценты в сказках
Проценты в сказках Кто хочет стать миллионером? 8 класс - Презентация по математике_
Кто хочет стать миллионером? 8 класс - Презентация по математике_ Степень с натуральным показателем
Степень с натуральным показателем Уравнение окружности
Уравнение окружности Теорема Пифагора
Теорема Пифагора Многранники в нашей жизни
Многранники в нашей жизни