Содержание
- 2. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ Линейная алгебра и аналитическая геометрия: 1. Матрицы 2. Определители 3. Системы линейных уравнений 4.
- 3. Линейная алгебра
- 5. Матрица – это прямоугольная таблица чисел. Аm*n – матрица размера m*n (m строк, n столбцов) bi
- 6. Виды матриц: Матрица-строка (вектор-строка) – матрица, состоящая из одной строки. Матрица-столбец – матрица, состоящая из одного
- 11. Операции над матрицами: Сложение – выполняется только для матриц одинакового размера. Умножение матрицы на число Транспонирование
- 12. Свойства операций над матрицами: переместительное свойство сочетательное свойство
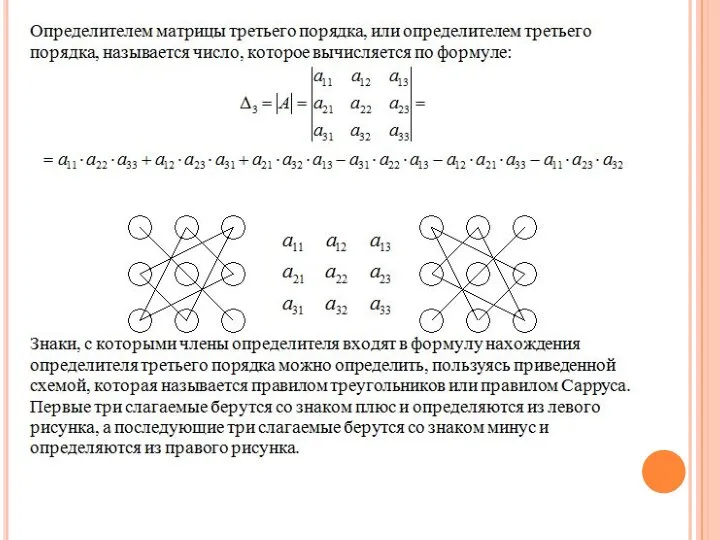
- 14. Определители Определитель – это число, характеризующее квадратную матрицу. Обозначение: Правила вычисления:
- 18. Правила вычисления определителя любого порядка Теорема Лапласа: Определитель квадратной матрицы равен сумме произведений элементов любой его
- 23. Обратная матрица Матрица А-1 называется обратной матрицей, если Алгоритм вычисления обратной матрицы А: Вычисляем определить матрицы
- 24. Решение систем линейных уравнений - переменные - коэффициенты при переменных - свободные коэффициенты Решить систему уравнений
- 26. Метод Крамера
- 27. 2 способ. Способ обратной матрицы Систему линейных уравнений можно представить в виде матричного уравнения где
- 28. Аналитическая геометрия Векторы на плоскости и в пространстве
- 29. Операции над векторами, заданными в координатной форме
- 30. Уравнение прямой на плоскости Уравнение прямой в общем виде Где А, В, С – числа. Уравнение
- 31. Условия параллельности и перпендикулярности прямых а, в – прямые k1, k2 – угловые коэффициенты прямых а
- 32. Аналитическая геометрия в пространстве Уравнение плоскости в пространстве, проходящей через точку M0 (x0 ; y0 ;
- 33. Уравнение прямой в пространстве Параметрическое: Каноническое: S (m; n; p) – направляющий вектор, M0 (x0 ;
- 34. Кривые второго порядка
- 38. Математический анализ
- 39. Функции Функцией (числовой функцией) называется отображение числового множества D в числовое множество Е. Функцию записывают так:
- 40. Предел переменной величины Предел – одно из основных понятий математического анализа. Понятие предела использовалось еще Ньютоном
- 41. Предел функции в точке Определение. Число b называется пределом функции в точке a, если для всех
- 42. Основные свойства пределов 1. Предел алгебраической суммы конченного числа переменных величин равен алгебраической сумме пределов слагаемых:
- 43. Замечательные пределы В математике важную роль играют два специальных предела, которые ввиду их важности названы «замечательными»:
- 44. Раскрытие неопределенностей Иногда правила предельного перехода непосредственно неприменимы. Например, при отыскании когда f(х)→0, φ(х) →0 или
- 45. Пример 4. Пример 5.
- 46. Дифференциальное исчисление Производной функции y=f (x) называется скорость изменения функции в данный момент времени (мгновенная скорость)
- 47. Правила дифференцирования
- 48. Пример. Вычислите производную функции
- 49. Применение производной к построению графика функции. Возрастание и убывание функции. Экстремумы. Функция y=f(x) возрастает на некотором
- 50. Промежутки выпуклости функции. Точки перегиба Функция y=f(x) на промежутке [a; b] Если вторая производная f”(x)>0, то
- 51. Пример. Исследовать функцию f(x) и построить ее график 1) Область определения R. 2) Функция непериодическая. 3)
- 52. 4) Точки пересечения с осью ОХ: y = 0
- 53. c осью OY: х = 0 ; у = -7\10
- 54. 5) Экстремумы, возрастание, убывание
- 56. 6) Выпуклость/вогнутость
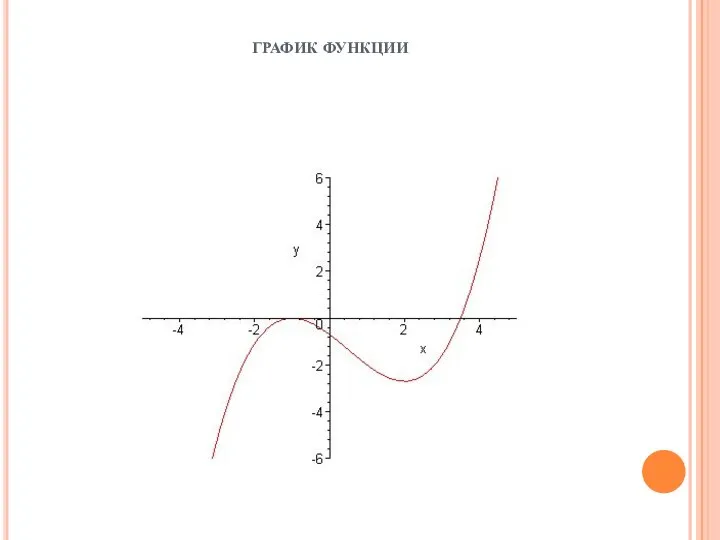
- 57. ГРАФИК ФУНКЦИИ
- 58. Первообразная и неопределенный интеграл
- 61. Производная неопределенного интеграла равна подынтегральной функции, а его дифференциал- подынтегральному выражению. Действительно:
- 62. Таблица неопределенных интегралов
- 63. Таблица неопределенных интегралов
- 64. Метод замены переменной
- 65. Примеры
- 66. Интегрирование по частям
- 67. Примеры
- 68. Определенный интеграл
- 69. Свойства определенного интеграла
- 70. Свойства определенного интеграла
- 71. Вычисление определенного интеграла
- 72. Пример Вычислить .
- 73. Вычисление интеграла
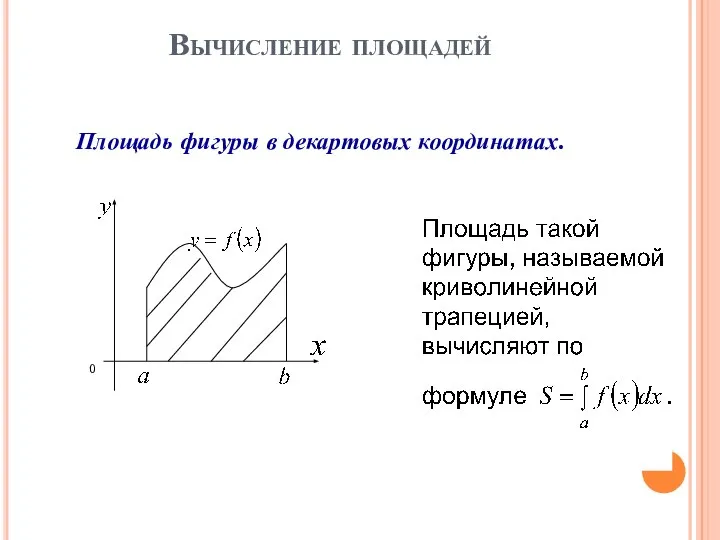
- 74. Вычисление площадей Площадь фигуры в декартовых координатах.
- 76. Скачать презентацию












































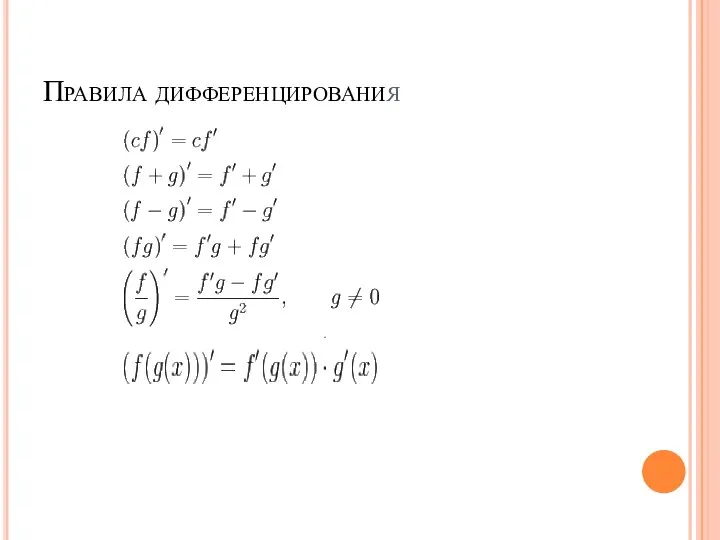


![Промежутки выпуклости функции. Точки перегиба Функция y=f(x) на промежутке [a; b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1458648/slide-49.jpg)






















 Аттестационная работа. Рабочая программа математического кружка в 5 классе: Математика плюс
Аттестационная работа. Рабочая программа математического кружка в 5 классе: Математика плюс Постороение сечений
Постороение сечений КАК ГОТОВИТЬСЯ к ГИА-9 по математике Учитель математики Воронина Т.К.
КАК ГОТОВИТЬСЯ к ГИА-9 по математике Учитель математики Воронина Т.К.  Задачи на железнодорожную тему
Задачи на железнодорожную тему Презентация по математике "Теорема косинусов в электронных таблицах" - скачать
Презентация по математике "Теорема косинусов в электронных таблицах" - скачать  Теорема Пифагора
Теорема Пифагора Статистика знает всё
Статистика знает всё Алгоритм решения квадратных неравенств
Алгоритм решения квадратных неравенств Площадь круга
Площадь круга Тема: « Задачи на построение сечений».
Тема: « Задачи на построение сечений».  Призма
Призма Пирамида в задачах ЕГЭ
Пирамида в задачах ЕГЭ Паркеты из многоугольников
Паркеты из многоугольников Касательная. Уравнение касательной
Касательная. Уравнение касательной Вводное повторение.Геометрия 8 класс
Вводное повторение.Геометрия 8 класс Туынды. Алғашқы функция. Интеграл
Туынды. Алғашқы функция. Интеграл Замечательный квадрат. Урок по математике в 5 классе
Замечательный квадрат. Урок по математике в 5 классе Геометрия. 7 класс
Геометрия. 7 класс Фунцияның туындысы мен дифференциалын қолдану
Фунцияның туындысы мен дифференциалын қолдану Линейные дискретные системы. Описание ЛДС во временной области
Линейные дискретные системы. Описание ЛДС во временной области Общая математическая модель динамики
Общая математическая модель динамики Подготовка к ГИА по математике. Задания 13
Подготовка к ГИА по математике. Задания 13 Как записывают и читают десятичные дроби
Как записывают и читают десятичные дроби Решение неравенств
Решение неравенств Объемы тел
Объемы тел Изучение взаимосвязи между явлениями методами корреляционно-регрессионного анализа
Изучение взаимосвязи между явлениями методами корреляционно-регрессионного анализа Геометрические иллюзии, или всегда ли мы видим то, что видим
Геометрические иллюзии, или всегда ли мы видим то, что видим Что такое процент
Что такое процент