Содержание
- 2. Логарифмы были придуманы для ускорения и упрощения вычислений. Идея логарифма, т. е. идея выражать числа в
- 3. ПОВТОРЕНИЕ Показательная функция, показательные уравнения Устно: an Основание степени Показатель степени
- 4. ПОВТОРЕНИЕ Показательная функция, показательные уравнения и неравенства. Устно: an Основание степени Показатель степени х = 2
- 5. ОПРЕДЕЛЕНИЕ Логарифмом по основанию а от аргумента x называют степень, в которую нужно возвести а, чтобы
- 6. ВАЖНЫЕ ФАКТЫ: 1.Аргумент и основание логарифма всегда должны быть больше нуля. Это следует из определения степени
- 7. Определение логарифма числа Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести
- 8. ОСНОВНОЕ ЛОГАРИФМИЧЕСКОЕ ТОЖДЕСТВО Равенство справедливо при b > 0, a > 0, a ≠ 1 5
- 9. Основные формулы
- 10. Вычислить
- 11. Вычислить
- 12. Вычислить
- 13. Вычислить
- 14. Выполнить устно
- 15. Выполнить устно =18 =14 =8
- 16. ДОКАЗАТЕЛЬСТВО:
- 17. ВЫЧИСЛИТЕ: ПРОВЕРКА:
- 18. Основные свойства логарифмов При любом a>0 (a≠1) и любых положительных x и y выполнены равенства: logₐ
- 19. Свойства логарифмов
- 20. Вычислить
- 21. Вычислить
- 22. Свойства логарифмов
- 23. Вычислить
- 24. Вычислить
- 25. Свойства логарифмов
- 26. Свойства логарифмов
- 27. Примеры
- 28. ВЫЧИСЛИТЕ: ПРОВЕРКА:
- 29. Проблема Обратите внимание - действия с логарифмами возможны только при одинаковых основаниях! А если основания разные!?
- 30. Переход к другому основанию Теорема Пусть дан логарифм loga b. Тогда для любого числа c такого,
- 31. Логарифмические уравнения
- 32. ОПРЕДЕЛЕНИЕ Логарифмом по основанию а от аргумента x называют степень, в которую нужно возвести а, чтобы
- 33. Воспользуемся сначала свойством Теперь перейдем к основанию 2
- 37. Логарифмическим уравнением называют уравнение, содержащее переменную под знаком логарифма Например: log2(x+6)=3 log3x=1-x Решить логарифмическое уравнение- это
- 38. Способы решения логарифмических уравнений На основании определения логарифма Логарифмом положительного числа b по положительному и отличному
- 39. Решить уравнение Log3(2x+1)=2 ОДЗ (ЗНАЮ!!!что существуют логарифмы только положительных чисел) 2x+1>0 2x+1=3² 2x=9-1 2x=8 x=4 Ответ
- 40. Простейшее логарифмическое уравнение Например:
- 41. Решить уравнения
- 42. №1. Решить уравнения
- 44. Решение уравнения под буквой в Согласно свойству: Назад
- 45. Решение уравнения под буквой г Назад
- 49. №1
- 50. №1
- 51. №2
- 52. №2
- 53. №3
- 54. №3
- 55. №4
- 56. №4
- 57. №5
- 58. №5
- 59. №6
- 60. №6
- 61. №7
- 62. №7
- 70. Скачать презентацию





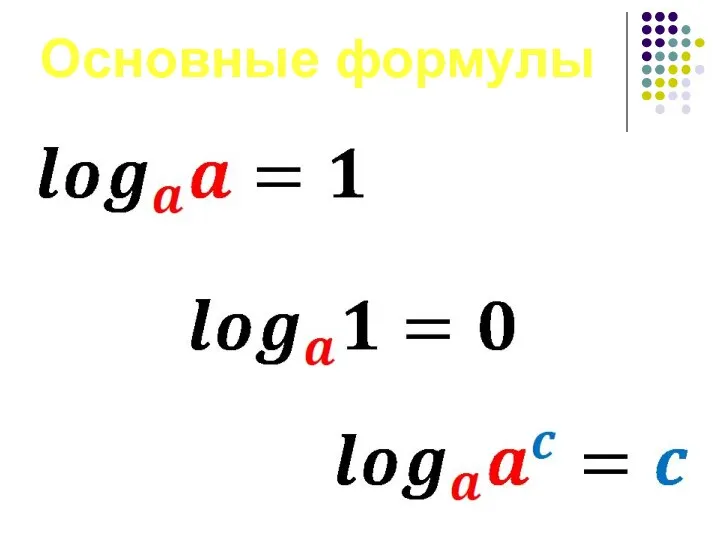

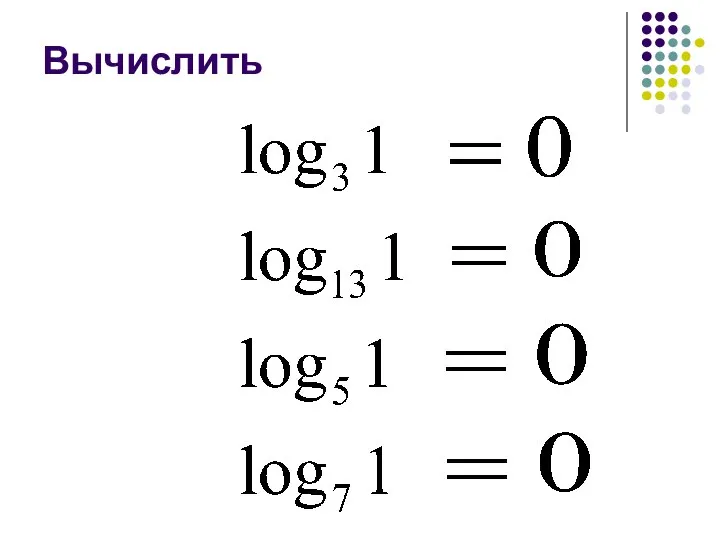
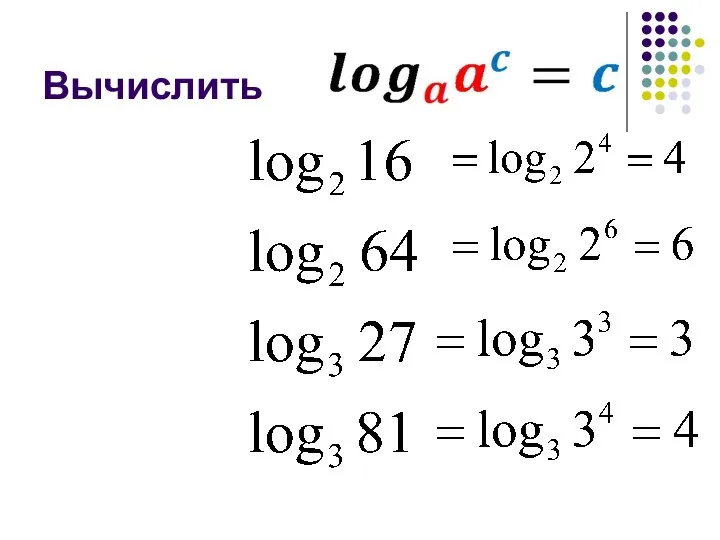
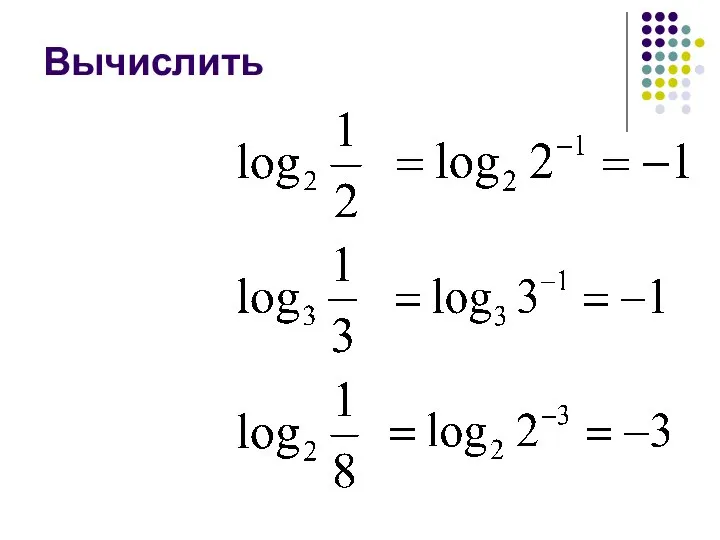











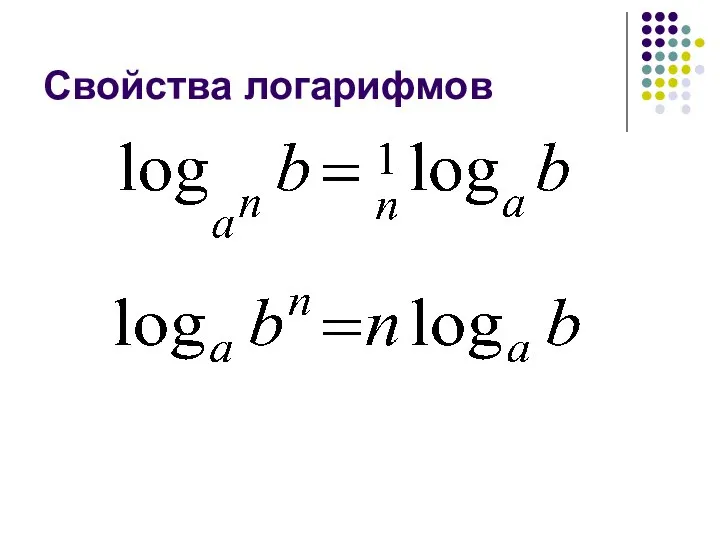


























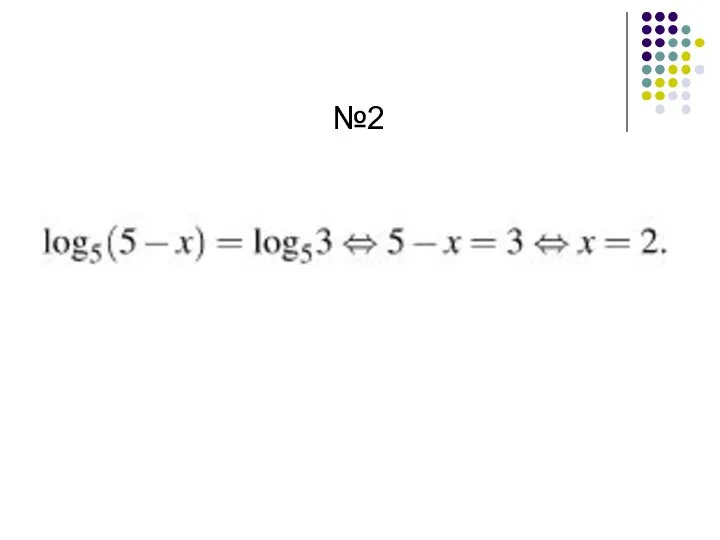



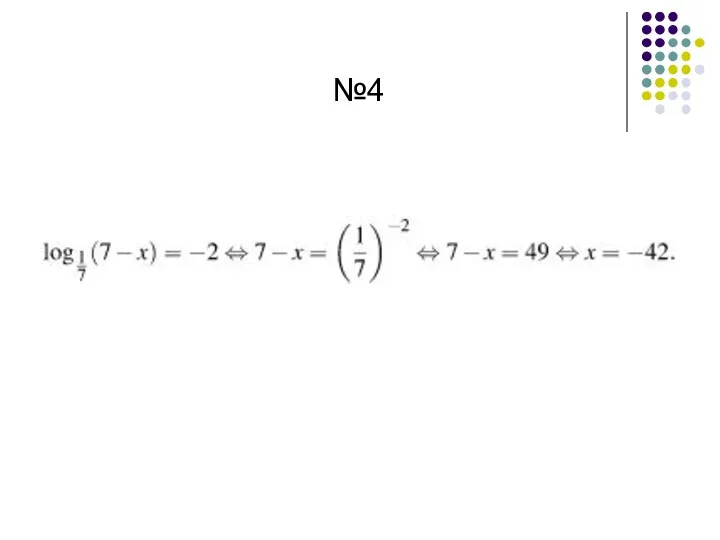

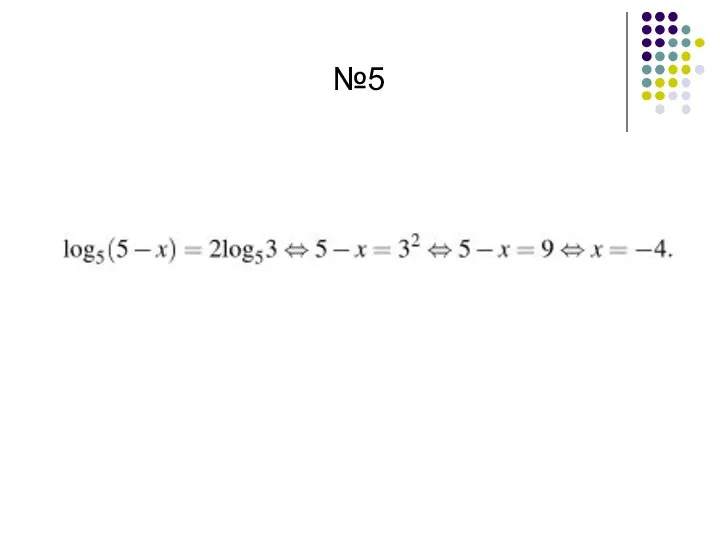



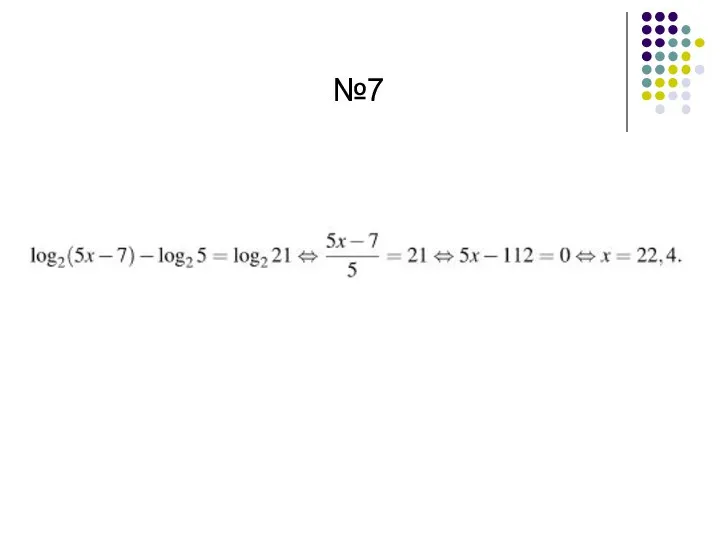



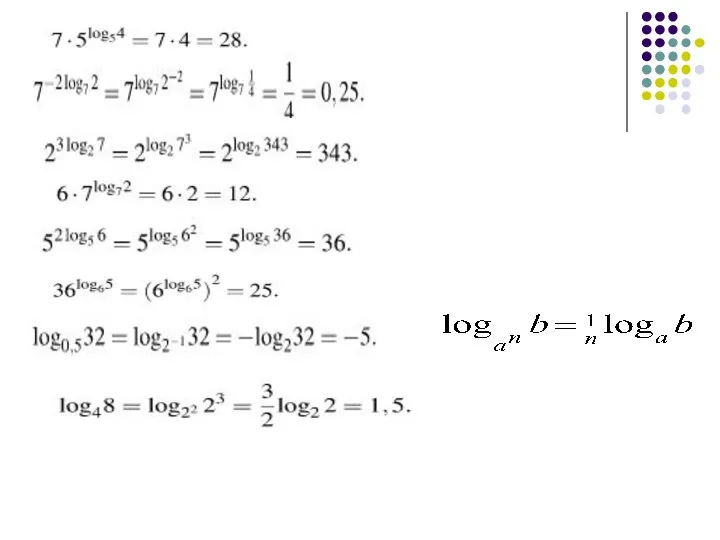
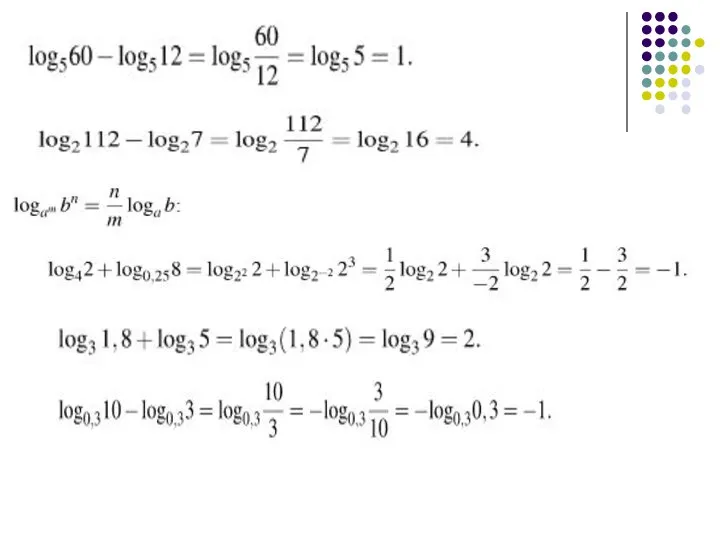
 Разложение на простые множители
Разложение на простые множители Презентация по математике "Приемы устного умножения и деления" - скачать
Презентация по математике "Приемы устного умножения и деления" - скачать  Разложение многочленов на множители
Разложение многочленов на множители Задачи в стихах. 1 касс
Задачи в стихах. 1 касс Задачи на проценты Автор работы Петрова Виктория Ученица 8а класса МАОУ СОШ п. Демянск
Задачи на проценты Автор работы Петрова Виктория Ученица 8а класса МАОУ СОШ п. Демянск Аттестационная работа. Все профессии важны, с математикой дружны
Аттестационная работа. Все профессии важны, с математикой дружны Упражнения для устного счёта по математике в 5 классе
Упражнения для устного счёта по математике в 5 классе Формы сокращенного умножения
Формы сокращенного умножения Презентация по математике "Виды часов" - скачать бесплатно
Презентация по математике "Виды часов" - скачать бесплатно Графики функций. Тесты. 9 класс
Графики функций. Тесты. 9 класс Возведение в степень произведения и степени
Возведение в степень произведения и степени Проектирование и нормализация базы данных
Проектирование и нормализация базы данных Презентация на тему Построение графика квадратичной функции Урок алгебры в 9 классе
Презентация на тему Построение графика квадратичной функции Урок алгебры в 9 классе  Вычисление производных
Вычисление производных Разность
Разность Длина окружности. Площадь круга
Длина окружности. Площадь круга Многогранники
Многогранники Принципы имитационного моделирования. Математические методы моделирования
Принципы имитационного моделирования. Математические методы моделирования Математическая викторина
Математическая викторина Элементы комбинаторики (обобщающий урок). 9 класс
Элементы комбинаторики (обобщающий урок). 9 класс Таблица умножения. Решение задач
Таблица умножения. Решение задач Площадь. Площадь четырехугольника
Площадь. Площадь четырехугольника Кездейсоқ шамалар
Кездейсоқ шамалар Методика изучения трехмерных геометрических фигур. Тела вращения
Методика изучения трехмерных геометрических фигур. Тела вращения Нестандартные способы математических вычислений
Нестандартные способы математических вычислений Презентация по математике "Помоги Незнайке" - скачать бесплатно
Презентация по математике "Помоги Незнайке" - скачать бесплатно Параллельность плоскостей
Параллельность плоскостей Задач на проценты
Задач на проценты