Содержание
- 2. Бронштейн Ефим Михайлович Кафедра вычислительной математики и кибернетики каб. 6-414а E-mail: bro-efim@yandex.ru
- 3. Литература 1. Ильин В.А., Позняк Э.Г. Основы математического анализа. Т.1-2. 2. Фихтенгольц Г.М. Курс дифференциального и
- 4. НЕКОТОРЫЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ ∀, ∃, ⇒ ∈, ∉, ∅,∩,∪, ⊂, ⊃ {x:R(x)} Необходимо - достаточно
- 5. ЗАГАДКА Продолжите последовательность О,Д,Т,Ч,П,Ш,…
- 6. ЧИСЛА Натуральные (N) Принцип математической индукции Утверждение R(n) для натуральных чисел. - R(1) истинно - R(n)
- 7. Примеры - 1+2+…+n=n(n+1)/2 - При x≥0 справедливо неравенство Бернулли (1+x)n≥1+nx
- 8. Целые (Z) Можно вычитать Рациональные (Q) можно делить (не на 0!) p/q Не существует рационального числа,
- 9. Вещественные (R) ±a0,a1a2…an… 1,000…00.. 0,999…999… Арифметические операции, сравнение ОПРЕДЕЛЕНИЕ 1. Множество X ограничено сверху, если ∃M
- 10. Пусть множество X ограничено сверху ОПРЕДЕЛЕНИЕ 2. Число M называется верхней гранью множества, если ∀x ∈X
- 11. ОПРЕДЕЛЕНИЕ 3. Точной верхней гранью ограниченного сверху множества X называется минимальная из верхних граней. Обозначение: sup
- 12. Иначе: 1.∀x ∈X (x≤sup X) 2. ∀ε>0 ∃x ∈X (x≥sup X−ε) Максимальный элемент множества max X
- 13. ТЕОРЕМА 1 (О точных гранях) У всякого ограниченного сверху множества ВЕЩЕСТВЕННЫХ чисел существует sup. У всякого
- 14. НЕКОТОРЫЕ ВИДЫ МНОЖЕСТВ (a,b) иное обозначение ]a,b[ - интервал [a,b] – отрезок, (a,b] - полуинтервал (−∞,+∞)
- 15. ТЕОРЕМА 2. Принцип вложенных отрезков. (Следствие из теоремы о точных гранях) Пусть [a1,b1]⊃[a2,b2]⊃…⊃[an,bn]⊃… Тогда ∩[an,bn]≠∅. Доказательство.
- 16. ПОСЛЕДОВАТЕЛЬНОСТИ И ИХ ПРЕДЕЛЫ ОПРЕДЕЛЕНИЕ 4. Пусть каждому натуральному числу ставится в соответствие некоторое вещественное число
- 17. Арифметические операции над последовательностями {хn}, {yn}: {хn+yn}, {хn-yn}, {хnyn}, {хn /yn} (при делении нужны оговорки), в
- 18. Примеры: 1) Последовательность —1, —4, —9, ... , —п2, ... Ограничена сверху и не ограничена снизу.
- 19. Бесконечно большие (ББ) последовательности ОПРЕДЕЛЕНИЕ 5. Последовательность {хn} называется бесконечно большой, если ∀M ∃N ∀n>N |хn|>M.
- 20. ПРИМЕРЫ Если хn=n, то хn→+∞ (N=⎡M⎤) Если хn=−n, то хn→−∞ Если хn=n(−1)n, то хn→∞ Связь с
- 21. БЕСКОНЕЧНО МАЛЫЕ (БМ) ПОСЛЕДОВАТЕЛЬНОСТИ ОПРЕДЕЛЕНИЕ 6. Последовательность {αп} называется бесконечно малой, если ∀ε>0 ∃N ∀n>N |αn|
- 22. ПРИМЕРЫ (ВАЖНЫЕ) 1. Последовательность q, q2, q3, ... , qn, ... - при |q| > 1
- 23. СВОЙСТВА БМП Сумма (разность) двух БМП есть БМП. Алгебраическая сумма любого конечного числа БМП — БМП.
- 24. СХОДЯЩИЕСЯ ПОСЛЕДОВАТЕЛЬНОСТИ ОПРЕДЕЛЕНИЕ 7. Последовательность {хп} называется сходящейся, если существует число a такое, что {хп-a} –
- 25. Иначе: ∃a∀ε>0 ∃N ∀n>N |хn-a| хn располагается в ε-окрестности числа (точки) a хп= a+αп, где αп-
- 26. ПРИМЕР: n/(n+1)→1 ПОСЛЕДОВАТЕЛЬНОСТЬ МОЖЕТ НЕ ИМЕТЬ ПРЕДЕЛА. Пример {(-1)n}
- 27. СВОЙСТВА СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ Сходящаяся последовательность имеет единственный предел. 2. Сходящаяся последовательность ограничена. (Обратное неверно.) 3. Сумма
- 28. Лемма. Если последовательность {уп} сходится и имеет отличный от нуля предел Ь, то, начиная с некоторого
- 29. ПРЕДЕЛЬНЫЙ ПЕРЕХОД В НЕРАВЕНСТВАХ ТЕОРЕМА 3. Если последовательность {хп} сходится и начиная с некоторого номера n
- 30. Следствие 2. Если элементы сходящихся последовательностей {хп} и {уп} начиная с некоторого номера удовлетворяют неравенству хп
- 31. ТЕОРЕМА 4. Пусть {хп} и {zn} — сходящиеся последовательности, имеющие общий предел а, и начиная с
- 32. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ ОПРЕДЕЛЕНИЕ 8. Последовательность {хп} называется неубывающей (невозрастающей), если каждый последующий член этой последовательности не
- 33. 1. Последовательность 1, 1, 1/2, 1/2, ... , 1/п, 1/п, ... невозрастающая. 2. Последовательность 1,1,2,2,...,п,п,... неубывающая.
- 34. ТЕОРЕМА 5. Неубывающая (невозрастающая) последовательность {хп}, ограниченная сверху (снизу), сходится. Замечание 1. Для монотонных последовательностей ограниченность
- 35. ПРИМЕР. X1=1, Xn+1=2Xn+1
- 36. ТЕОРЕМА 6. Последовательность сходится. К доказательству. Последовательность убывающая. Предел последовательности из теоремы 6 обозначается e.
- 37. Подпоследовательность. ТЕОРЕМА 7.(Больцано-Вейерштрасса). Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
- 38. ОПРЕДЕЛЕНИЕ 9. Последовательность {хп} называется фундаментальной, если для ∀ε>0 ∃N ∀n>N ∀p|хn-хn+p| ТЕОРЕМА 8. (Критерий Коши)
- 40. Скачать презентацию











![НЕКОТОРЫЕ ВИДЫ МНОЖЕСТВ (a,b) иное обозначение ]a,b[ - интервал [a,b] –](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/748243/slide-13.jpg)




















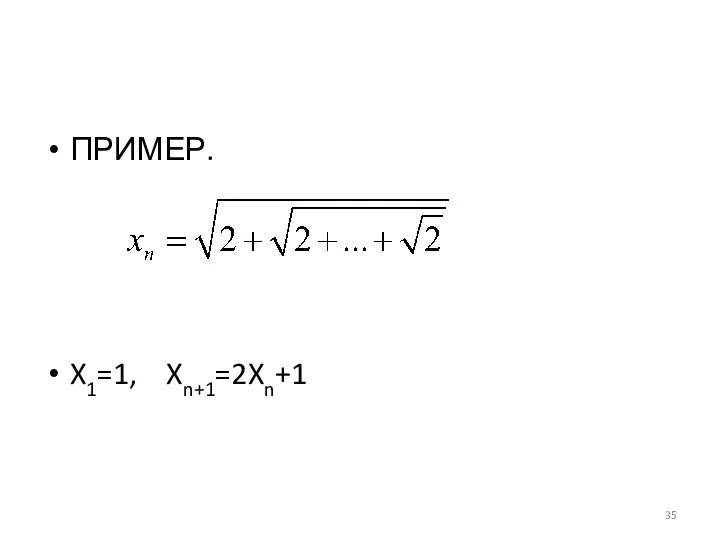



 Активизация познавательной деятельности на уроках математики
Активизация познавательной деятельности на уроках математики Развитие словесно-логического мышления младших школьников на уроках математики
Развитие словесно-логического мышления младших школьников на уроках математики Тренажёр по математике 1 класс. Сложение и вычитание в пределах 10
Тренажёр по математике 1 класс. Сложение и вычитание в пределах 10 Преобразование графиков функций
Преобразование графиков функций МОУ Приаргунская Средняя Общеобразовательная Школа Выполнил : Ученик 6а класса Дворцов Павел Руководитель Капишулина Ирина Ми
МОУ Приаргунская Средняя Общеобразовательная Школа Выполнил : Ученик 6а класса Дворцов Павел Руководитель Капишулина Ирина Ми Параллельные алгоритмы вычислительной алгебры. Современные компьютеры
Параллельные алгоритмы вычислительной алгебры. Современные компьютеры Математика в реальной жизни
Математика в реальной жизни Геометрия Лобачевского
Геометрия Лобачевского Десятичная запись дробных чисел
Десятичная запись дробных чисел Игра-зачет "Четырехугольники"
Игра-зачет "Четырехугольники" Делимость целых чисел
Делимость целых чисел Динамика 2D - изображения
Динамика 2D - изображения Неравенства с двумя переменными и их системы
Неравенства с двумя переменными и их системы Свойства степени с рациональным показателем
Свойства степени с рациональным показателем Числовые последовательности. Арифметическая прогрессия. Геометрическая прогрессия
Числовые последовательности. Арифметическая прогрессия. Геометрическая прогрессия Первообразная. Неопределенный интеграл
Первообразная. Неопределенный интеграл Моделирование случайных событий
Моделирование случайных событий Линейная функция и её график
Линейная функция и её график Занимательная математика для детей. Устный счёт, учимся писать цифры
Занимательная математика для детей. Устный счёт, учимся писать цифры Выработка вычислительных навыков Учитель математики МОУ «СОШ№ 8» Швецова Елена Владимировна
Выработка вычислительных навыков Учитель математики МОУ «СОШ№ 8» Швецова Елена Владимировна Статистическая сводка и группировка данных
Статистическая сводка и группировка данных Types of vectors
Types of vectors Системы линейных уравнений с двумя переменными. Терминологический словарь
Системы линейных уравнений с двумя переменными. Терминологический словарь Линейная функция и ее график
Линейная функция и ее график Использование технологии проблемного диалога, формирующего навыки исследовательской деятельности на уроках математики
Использование технологии проблемного диалога, формирующего навыки исследовательской деятельности на уроках математики Дисперсионный анализ Докладчик: ординатор Хамаева А.А.
Дисперсионный анализ Докладчик: ординатор Хамаева А.А. Урок информатики в 3-м классе Учитель: Кветковский Алексей Витальевич
Урок информатики в 3-м классе Учитель: Кветковский Алексей Витальевич  Простая арифметическая задача
Простая арифметическая задача