Содержание
- 2. Основные вопросы: Определение первообразной. Основное свойство первообразной. Понятие неопределенного интеграла. Основные формулы интегрирования. Непосредственное интегрирование (метод
- 3. Определение первообразной. Основное свойство первообразной. Первообразной функцией по отношению к данной функции у = f(x) называется
- 4. Понятие неопределенного интеграла. Основные формулы интегрирования Совокупность всех первообразных F(x) + С для данной функции у
- 5. Геометрический смысл неопределенного интеграла. Геометрически, неопределенный интеграл представляет собой семейство интегральных кривых на плоскости, полученных путем
- 6. поскольку функция - первообразная для функции х4. Процесс нахождения неопределенного интеграла функции называется интегрированием этой функции.
- 7. Свойства неопределенного интеграла: 1. Производная неопределенного интеграла равна подынтегральной функции: Это свойство считается очень важным, его
- 8. 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению: Свойства неопределенного интеграла:
- 9. 3. Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная: Свойства неопределенного интеграла:
- 10. 4.Постоянный множитель можно выносить за знак неопределенного интеграла: Свойства неопределенного интеграла:
- 11. 5.Неопределенный интеграл от суммы 2-х функций равен сумме неопределенных интегралов от этих функций: Свойства неопределенного интеграла:
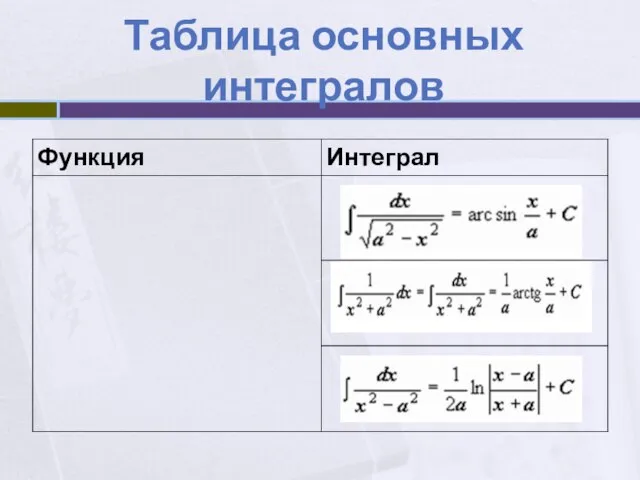
- 12. Таблица основных интегралов
- 13. Таблица основных интегралов
- 14. Таблица основных интегралов
- 15. Таблица основных интегралов
- 16. Таблица основных интегралов
- 17. Основные методы интегрирования
- 18. 1.Непосредственное интегрирование
- 19. Непосредственное интегрирование – это метод, основанный на применении тождественных преобразований подынтегральной функции, а также основных свойств
- 20. Непосредственное интегрирование Наиболее часто используются следующие преобразования подынтегральной функции: Деление числителя на знаменатель почленно; Применение формул
- 22. Найти неопределенный интеграл методом непосредственного интегрирования. Используя свойство неопределенного интеграла, вынесем за знак интеграла постоянный множитель.
- 23. Решение:
- 25. Решение:
- 26. Решение:
- 28. 2. Метод подстановки
- 29. Замена переменной (метод подстановки) Чаще всего этот метод используется, если в подынтегральном выражении содержится сложная функция,
- 30. НАПРИМЕР Далее необходимо выполнить следующие действия: Найти дифференциал новой переменной ; Записать прежний интеграл, используя только
- 31. Найти Решение: введем подстановку u = 5x + 3 дифференциал этого выражения: d (5x + 3)
- 32. Заменив u его выражением через x, имеем: Проверка: Интеграл найден правильно.
- 33. Решение: Заменяя переменную в данном интеграле, имеем: Подставляя вместо t его выражение через x, найдем:
- 35. Найти неопределенный интеграл, используя метод замены переменной. Сделаем замену переменной t = sin x, тогда dt
- 36. Сделав обратную замену, получим окончательный ответ: Ответ:
- 37. Решение:
- 38. Решение:
- 39. 3. Интегрирование по частям
- 40. Метод интегрирования по частям – это метод, заключающийся в использовании формулы:
- 41. Данный метод интегрирования основан на тождестве: где u = f(x) и v = φ(x) - две
- 42. Решение:
- 43. Ответ:
- 44. Решение: Ответ:
- 45. Интегрирование некоторых тригонометрических функций.
- 46. Интегралы от произведений синусов и косинусов с разными аргументами, линейно зависящими от , упрощаются, если применить
- 47. Вычислим интеграл Преобразуем произведение в сумму: тогда
- 48. Домашнее задание: Колесов В.В. Математика для медицинских колледжей: учебное пособие/В.В.Колесов, М.Н. Романов. – Ростов н/Д: Феникс,
- 50. Скачать презентацию














































 Функции комплексного переменного
Функции комплексного переменного Математика 1 класс. Сложение с переходом через десяток
Математика 1 класс. Сложение с переходом через десяток Презентация на тему Виды параллелограмма
Презентация на тему Виды параллелограмма  Презентация по математике "Деление числа с остатком. Обобщение" - скачать
Презентация по математике "Деление числа с остатком. Обобщение" - скачать  Векторное пространство
Векторное пространство Интегрированный урок истории и математики. 27 января - снятие блокады Ленинграда
Интегрированный урок истории и математики. 27 января - снятие блокады Ленинграда Модуль числа. 6 класс
Модуль числа. 6 класс Сложение и вычитание двузначных чисел
Сложение и вычитание двузначных чисел Выпуклый анализ. Минимум выпуклой функции. Лекция 16
Выпуклый анализ. Минимум выпуклой функции. Лекция 16 Признаки сходимости несобственных интегралов. Теорема 1. Признак сравнения несобственных интегралов 1 рода
Признаки сходимости несобственных интегралов. Теорема 1. Признак сравнения несобственных интегралов 1 рода Симметрия
Симметрия Системы линейных уравнений с двумя переменными Работа устно
Системы линейных уравнений с двумя переменными Работа устно Сравнение смешанных дробей
Сравнение смешанных дробей Презентация по математике "Вычитание натуральных чисел" - скачать
Презентация по математике "Вычитание натуральных чисел" - скачать  Презентация на тему основное свойство дроби
Презентация на тему основное свойство дроби Методы интегрирования
Методы интегрирования Комплексные числа
Комплексные числа Основы оптимизации перевозочного процесса. Методы маршрутизации перевозок грузов
Основы оптимизации перевозочного процесса. Методы маршрутизации перевозок грузов Решение уравнений, содержащих знак абсолютной величины Автор: Хохлачева Мария Сергеевна, 8 «В» класс МОУ СОШ № 3 г.Волгограда
Решение уравнений, содержащих знак абсолютной величины Автор: Хохлачева Мария Сергеевна, 8 «В» класс МОУ СОШ № 3 г.Волгограда Дидактическая игра по математике для 1 класса «Заселяем домики» /повторение и закрепление знаний состава чисел первого десят
Дидактическая игра по математике для 1 класса «Заселяем домики» /повторение и закрепление знаний состава чисел первого десят Интегрированный урок математики, окружающего мира и музейной педагогики Тема: «Умножение и деление на 2. Решение задач и выраж
Интегрированный урок математики, окружающего мира и музейной педагогики Тема: «Умножение и деление на 2. Решение задач и выраж Презентация по математике "Золотое сечение на Новгородчине" - скачать
Презентация по математике "Золотое сечение на Новгородчине" - скачать  Сложение и вычитание натуральных чисел
Сложение и вычитание натуральных чисел Презентация по математике "Выражения" - скачать бесплатно
Презентация по математике "Выражения" - скачать бесплатно Задачи и методы математической статистики. Выборочный метод
Задачи и методы математической статистики. Выборочный метод Кривые второго порядка
Кривые второго порядка Теорема Эйлера Автор работы: Ужга Андрей ученик 10 класса МОУ.СОШ. п.Донское Руководитель: Шинкоренко Т.П. учитель алгебры и геоме
Теорема Эйлера Автор работы: Ужга Андрей ученик 10 класса МОУ.СОШ. п.Донское Руководитель: Шинкоренко Т.П. учитель алгебры и геоме Перпендикулярность плоскостей. Параллелепипед
Перпендикулярность плоскостей. Параллелепипед