Содержание
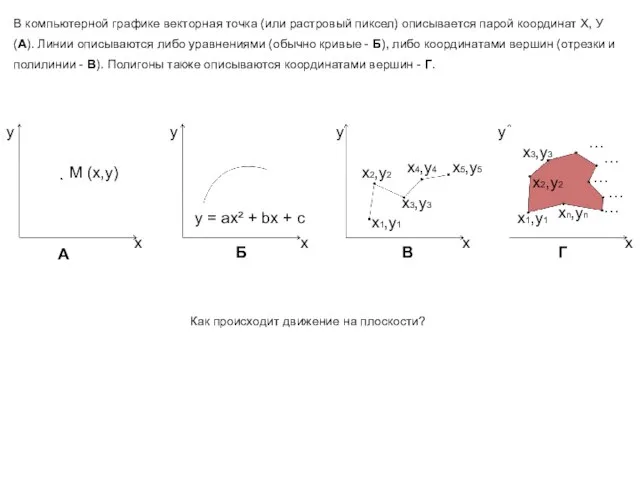
- 2. В компьютерной графике векторная точка (или растровый пиксел) описывается парой координат Х, У(А). Линии описываются либо
- 3. Существует 4 простейших преобразования, с помощью которых можно представить движение: параллельный перенос; вращение; растяжение – сжатие;
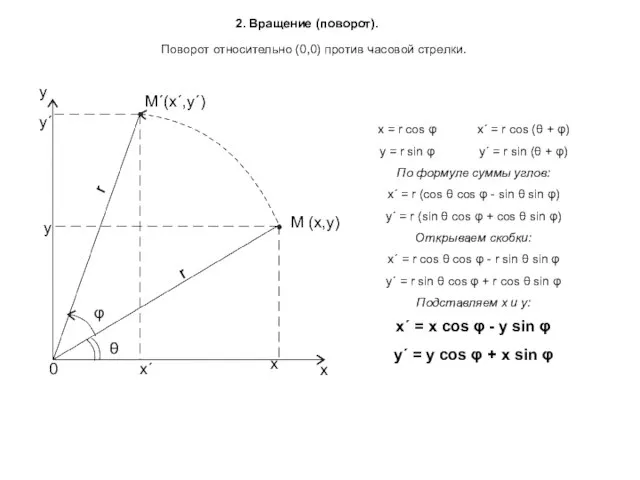
- 4. 2. Вращение (поворот). М (х,у) М΄(х΄,у΄) x y 0 φ θ r r х΄ x y
- 5. 3. Зеркальное отражение. а). Отражение относительно ОХ б). Отражение относительно ОУ у х΄ = x у΄
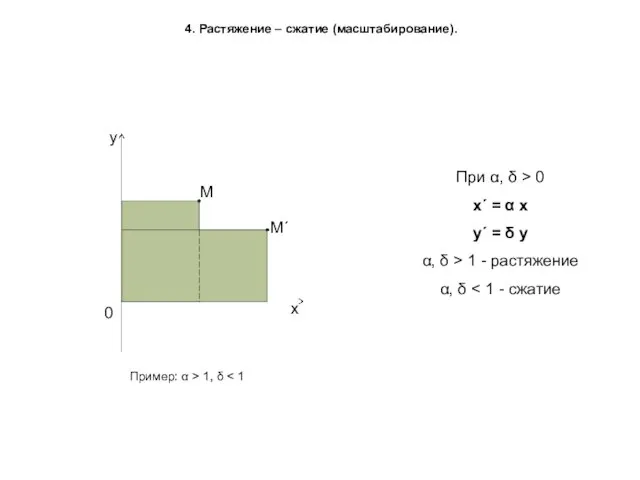
- 6. 4. Растяжение – сжатие (масштабирование). При α, δ > 0 х΄ = α x у΄ =
- 7. С помощью 4 простейших преобразований происходит простое движение на плоскости – когда мы заранее знаем каково
- 8. Полиномиальные преобразования Каково будет движение (перемещение) известно не всегда. Иногда есть лишь координаты нескольких точек до
- 9. Аффинное преобразование Это уравнение координат, включающее в себя все 4 простейших преобразований плоскости: х΄ = αx
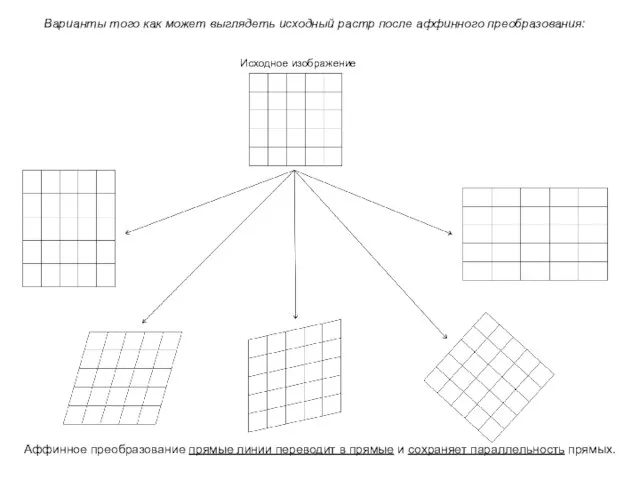
- 10. Варианты того как может выглядеть исходный растр после аффинного преобразования: Аффинное преобразование прямые линии переводит в
- 11. Проективное преобразование Также полином 1-й степени. х΄ = αx + βу + a / d у΄
- 12. Степенные полиномы Не всегда растр можно привязать с помощью полиномов 1-й степени. Особенно сложно это сделать
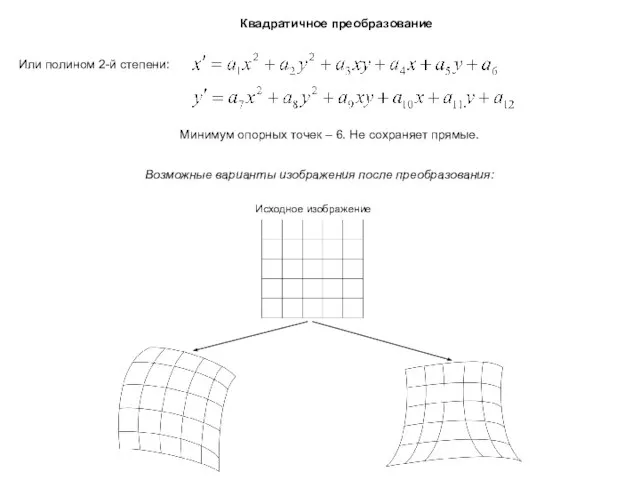
- 13. Квадратичное преобразование Или полином 2-й степени: Минимум опорных точек – 6. Не сохраняет прямые. Возможные варианты
- 14. Полиномы 5-й степени Максимальная степень полинома, используемая на практике для трансформаций. Формулы опустим. Минимальное количество опорных
- 16. Скачать презентацию








 Решение задач, приводящих к умножению дробей
Решение задач, приводящих к умножению дробей Тренажёр-раскраска «Нумерация чисел от 21 до 100»
Тренажёр-раскраска «Нумерация чисел от 21 до 100» Cхема (метод) Горнера. Способ деления многочлена
Cхема (метод) Горнера. Способ деления многочлена Аттестационная работа. Разработка урока «Решение задач на применение второго признака равенства треугольников» 7 класс
Аттестационная работа. Разработка урока «Решение задач на применение второго признака равенства треугольников» 7 класс Числовые промежутки. 8 класс
Числовые промежутки. 8 класс Ошибка измерения. Учет ошибки шкалы прибора и систематических ошибок. Оценка суммарной погрешности
Ошибка измерения. Учет ошибки шкалы прибора и систематических ошибок. Оценка суммарной погрешности Работа с текстовой математической задачей
Работа с текстовой математической задачей Тема: «Положительные и отрицательные числа» 6 класс Урок обобщения и систематизации знаний Презентацию выполнила: Черкасо
Тема: «Положительные и отрицательные числа» 6 класс Урок обобщения и систематизации знаний Презентацию выполнила: Черкасо Комбинаторика. Правило суммы и правило произведения
Комбинаторика. Правило суммы и правило произведения Операції диференціювання. Первісна функція
Операції диференціювання. Первісна функція Решение показательного уравнения
Решение показательного уравнения Порядок выполнения действий
Порядок выполнения действий Делимость чисел
Делимость чисел Сумма углов треугольника ГБОУ СОШ №1358 УЧИТЕЛЬ МАТЕМАТИКИ ЕПИФАНОВА ТАТЬЯНА НИКОЛАЕВНА
Сумма углов треугольника ГБОУ СОШ №1358 УЧИТЕЛЬ МАТЕМАТИКИ ЕПИФАНОВА ТАТЬЯНА НИКОЛАЕВНА  Одночлен и его стандартный вид. 7 класс
Одночлен и его стандартный вид. 7 класс Полезные функции
Полезные функции Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Osnovy_teorii_veroyatnostey
Osnovy_teorii_veroyatnostey Аттестационная работа. Образовательная программа внеурочной деятельности. Создаем проекты по математики. (5 класс)
Аттестационная работа. Образовательная программа внеурочной деятельности. Создаем проекты по математики. (5 класс) Прямоугольный и треугольные обходы
Прямоугольный и треугольные обходы Сложная функция. 10 класс
Сложная функция. 10 класс Непараметрический дисперсионный анализ
Непараметрический дисперсионный анализ Признаки равенства треугольников
Признаки равенства треугольников 11г 12.09
11г 12.09 Построение треугольника
Построение треугольника Взаимно обратные числа. Урок № 1. 6 класс
Взаимно обратные числа. Урок № 1. 6 класс Математические ребусы
Математические ребусы Логическая модель. Логика высказываний. Основы логики высказываний
Логическая модель. Логика высказываний. Основы логики высказываний