Математика. Управление социальными системами. Тема 2. Элементы аналитической геометрии

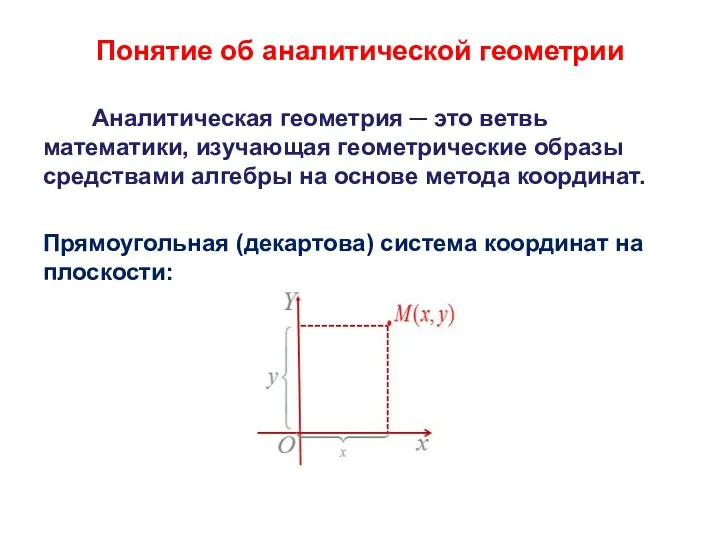
Понятие об аналитической геометрии

Аналитическая геометрия ─ это ветвь математики, изучающая геометрические

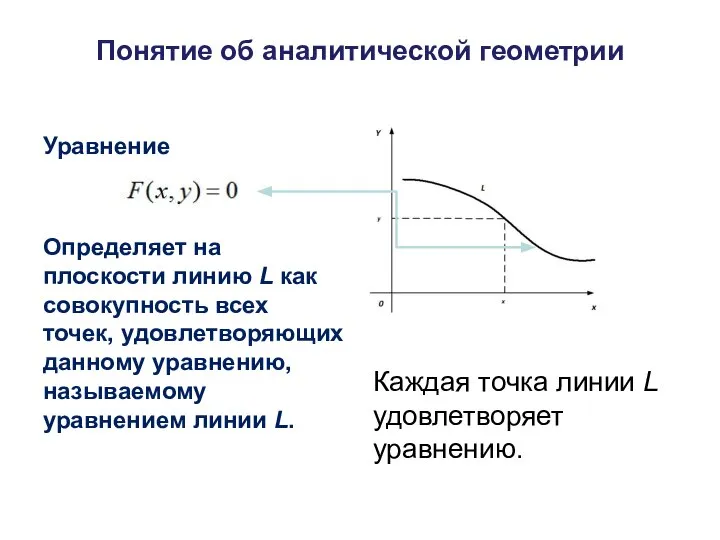
Понятие об аналитической геометрии

Уравнение
Определяет на плоскости линию L как совокупность всех

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

Уравнения прямой на плоскости
1) Уравнение прямой с угловым коэффициентом:

Уравнения прямой на плоскости

2) Уравнение прямой, проходящей через заданную точку M(x1;y1)

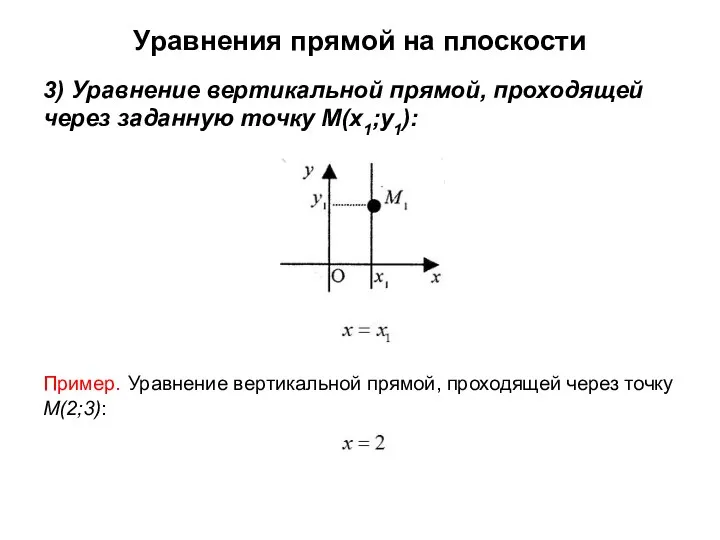
Уравнения прямой на плоскости

3) Уравнение вертикальной прямой, проходящей через заданную точку

Уравнения прямой на плоскости

4) Уравнение прямой, проходящей через две заданные точки

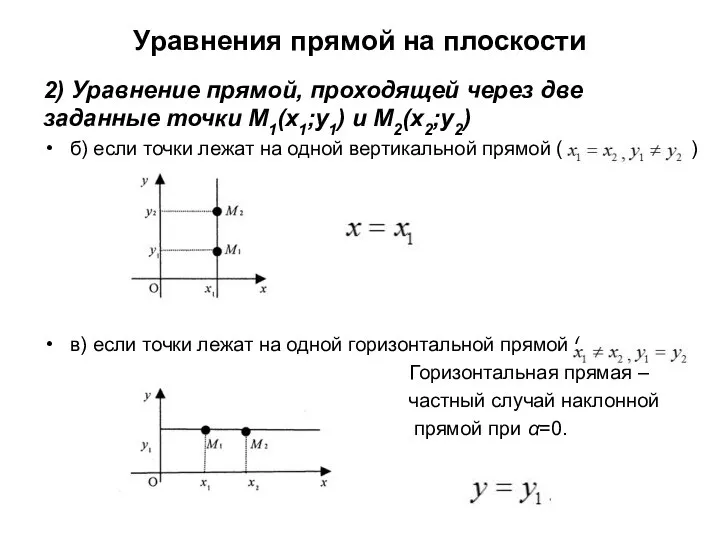
Уравнения прямой на плоскости

2) Уравнение прямой, проходящей через две заданные точки

Уравнения прямой на плоскости
Следствие:
Угловой коэффициент прямой, проходящей через две заданные точки

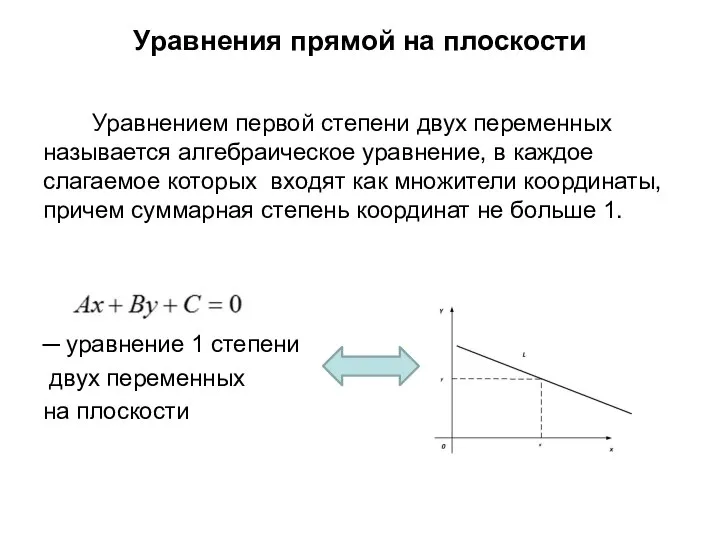
Уравнения прямой на плоскости
5) Общее уравнение прямой на плоскости:
причем коэффициенты А

Уравнения прямой на плоскости
Уравнением первой степени двух переменных называется алгебраическое уравнение,

Уравнения прямой на плоскости
6) Уравнение прямой «в отрезках»:
Пример. Уравнение
можно представить

Приложения
1) Необходимое и достаточное условие параллельности прямых с угловыми коэффициентами k1

Приложения
3) Острый угол φ между прямыми, заданными уравнениями :

Элементы аналитической геометрии в пространстве

Уравнения плоскости
а)

Уравнения плоскости

б) Общее уравнение плоскости

Расстояние от точки до плоскости

Найти расстояние d от точки M(x0; y0;

Расположение плоскостей

Расположение плоскостей

Кривые второго порядка

При изучении линий на плоскости их классифицируют по сложности

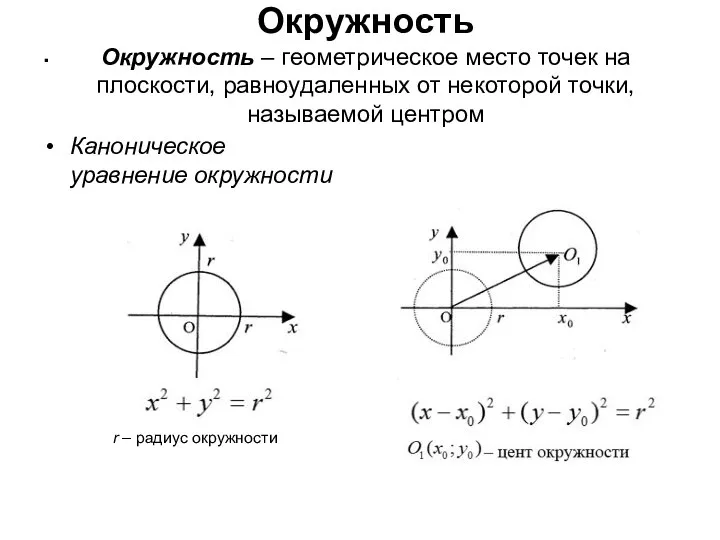
Окружность Окружность – геометрическое место точек на плоскости, равноудаленных от некоторой точки,

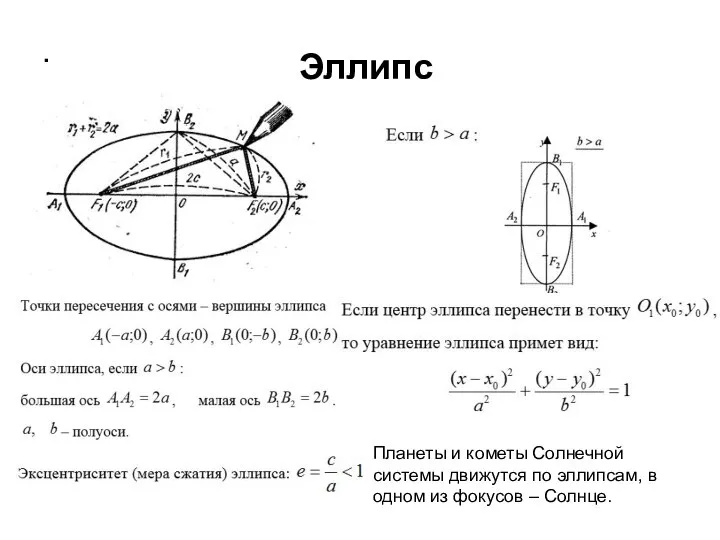
Эллипс Эллипс – геометрическое место точек на плоскости, для каждой из которых

Эллипс

.
Планеты и кометы Солнечной системы движутся по эллипсам, в одном из

Гипербола Гипербола – геометрическое место точек на плоскости, для каждой из которых

Гипербола

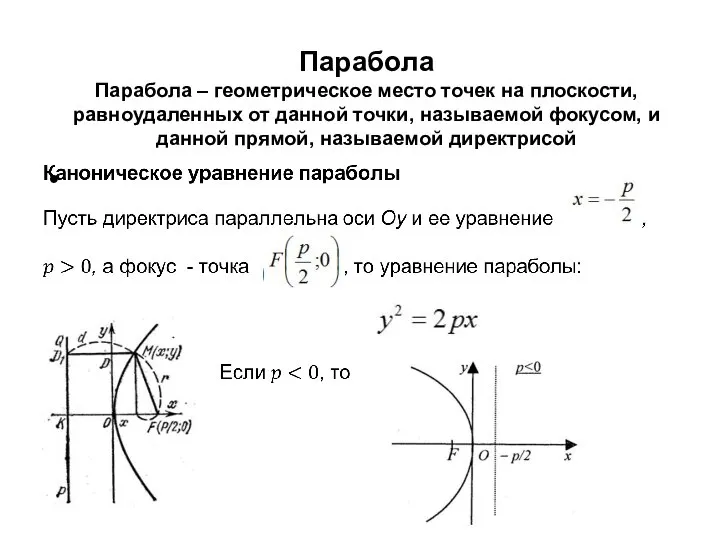
Парабола Парабола – геометрическое место точек на плоскости, равноудаленных от данной точки,

Парабола

Если директриса параллельна оси Ox :
Если вершину параболы перенести в точку

Общий вид уравнения кривой второго порядка

Приведение уравнения кривой к каноническому виду

Основной прием – выделение полных квадратов.