Содержание
- 2. Some terminology A theorem is a statement that can be shown to be true. In mathematical
- 3. Терминология We demonstrate that a theorem is true with a proof. A proof is a valid
- 4. Some terminology The statements used in a proof can include axioms (or postulates), which are statements
- 5. Some terminology Axioms may be stated using primitive terms that do not require definition, but all
- 6. Some terminology Rules of inference, together with definitions of terms, are used to draw conclusions from
- 7. Some terminology A less important theorem that is helpful in the proof of other results is
- 8. Some terminology A corollary is a theorem that can be established directly from a theorem that
- 9. Some terminology A conjecture is a statement that is being proposed to be a true statement,
- 10. Methods of proof In practice, the proofs of theorems designed for human consumption are almost always
- 11. Methods of proof Informal proofs can often explain to humans why theorems are true, while computers
- 12. Methods of proof The methods of proof discussed here are important not only because they are
- 13. Methods of proof Consequently, understanding the techniques used in proofs is essential both in mathematics and
- 14. Methods of proof
- 15. Methods of proof There are several standard methods of proof, including the following: direct argument, contrapositive
- 16. Direct argument
- 17. Contrapositive argument
- 18. Proof by contradiction
- 19. Example 1 Use a direct method of proof to show that if х and у are
- 20. Example 2 Let n be a positive integer. Prove, using the contrapositive, that if n2 is
- 21. Example 3 Use a proof by contradiction to show that if x2 = 2 then x
- 22. Example 3 Use a proof by contradiction to show that if x2 = 2 then x
- 23. Mathematical induction In computing a program is said to be correct if it behaves in accordance
- 24. Mathematical induction Consider the following recursive algorithm, intended to calculate the maximum element in a list
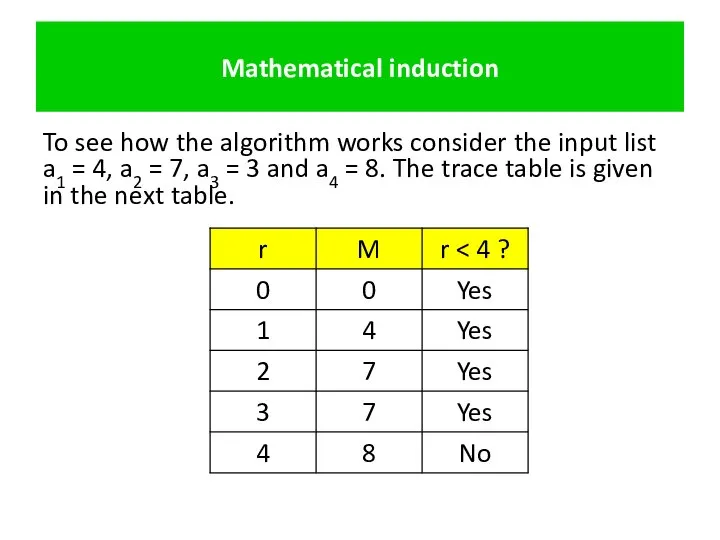
- 25. Mathematical induction To see how the algorithm works consider the input list a1 = 4, a2
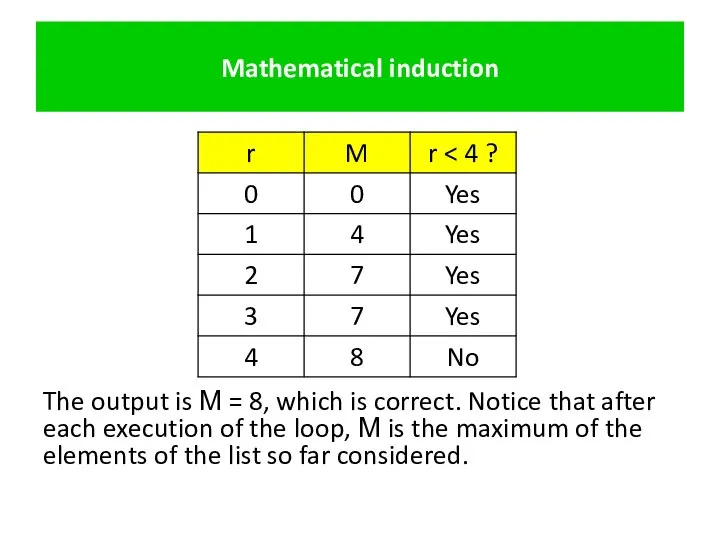
- 26. Mathematical induction The output is М = 8, which is correct. Notice that after each execution
- 27. Mathematical induction So does the algorithm for all lists of any length n? Consider an input
- 28. Mathematical induction By condition 1) the algorithm works for any list of length 1, and so
- 29. Mathematical induction
- 30. Mathematical induction
- 31. Mathematical induction
- 32. Mathematical induction
- 33. Mathematical induction
- 34. Mathematical induction Example 3 A sequence of integers x1, x2, …, xn is defined recursively as
- 36. Скачать презентацию































 Теория вероятностей
Теория вероятностей Число и цифра 9
Число и цифра 9 Золотое сечение. Числа Фибоначчи
Золотое сечение. Числа Фибоначчи Аттестационная работа. Математика вокруг нас. Числа в загадках, пословицах и поговорках. (1 класс)
Аттестационная работа. Математика вокруг нас. Числа в загадках, пословицах и поговорках. (1 класс) Наибольший общий делитель и наименьшее общее кратное чисел
Наибольший общий делитель и наименьшее общее кратное чисел История открытия комплексных чисел
История открытия комплексных чисел Сумма углов треугольника открытый урок геометрии в 6Б классе МОУ «СОШ №20 им. Васьлея Митты с углубленным изучением отдельных
Сумма углов треугольника открытый урок геометрии в 6Б классе МОУ «СОШ №20 им. Васьлея Митты с углубленным изучением отдельных Окружность. Примеры решения задач. Подготовка к ОГЭ
Окружность. Примеры решения задач. Подготовка к ОГЭ Определение автокорреляции
Определение автокорреляции Объем конуса цилиндра
Объем конуса цилиндра Теория множеств. Понятие множества
Теория множеств. Понятие множества Интегрированный урок. Применение производной в физике и технике. 11 класс
Интегрированный урок. Применение производной в физике и технике. 11 класс Векторы. Векторные величины
Векторы. Векторные величины Взаимное расположение графиков линейных функций (алгебра 7 класс)
Взаимное расположение графиков линейных функций (алгебра 7 класс) Теорема. Площадь трапеции
Теорема. Площадь трапеции Умножаем и делим на 10. 2 класс
Умножаем и делим на 10. 2 класс Диаграммы. Задачи
Диаграммы. Задачи Функции. Различные способы задания функции
Функции. Различные способы задания функции Неполный факторный план. Дробные реплики
Неполный факторный план. Дробные реплики Интерполирование функций. Интерполяционный многочлен Лагранжа
Интерполирование функций. Интерполяционный многочлен Лагранжа Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Математика в фокусах
Математика в фокусах Отношения следования и равносильности
Отношения следования и равносильности Четырёхугольники
Четырёхугольники Линейная алгебра. Билинейные и квадратичные формы. (Часть 14)
Линейная алгебра. Билинейные и квадратичные формы. (Часть 14) Таблица умножения на 2-10
Таблица умножения на 2-10 Проецирование правильных треугольных и шестиугольных призм
Проецирование правильных треугольных и шестиугольных призм Координатная плоскость
Координатная плоскость