Содержание
- 2. МЕТОДИ РОЗВ’ЯЗУВАННЯ СЛАР Методи чисельного розв’язування СЛАР діляться на дві групи: прямі та ітераційні. В прямих
- 4. ПРЯМІ МЕТОДИ РОЗВ’ЯЗУВАННЯ СЛАР МЕТОД ГАУССА Прямий хід методу Гаусса полягає в послідовному виключенні невідомих x1,x2,…,xn
- 5. МЕТОД ГАУССА Коефіцієнти системи обчислюються за формулами: Обчислення правих частин системи здійснюється за формулами:
- 6. МЕТОД ГАУССА Виключаючи послідовно невідомі із початкової системи отримуємо систему рівнянь Cx = y: Зворотній хід
- 7. МЕТОД ГАУССА Метод Гаусса має сигнальну функцію виду (поліноміальний): Елемент називається ведучим елементом на k-му кроці
- 8. Матрицею перестановок P називається квадратна матриця, у якої в кожному рядку і в кожному стовпці наявний
- 9. З системи Ax = b маємо Cx = y Можна показати b та y пов’язані між
- 10. Метод Гаусса відповідає розкладанню матриці A на добуток двох трикутних матриць: A = LU (L =
- 11. LU-розкладання матриці А
- 12. Приклад
- 13. Схема Холецького Самостійно: розглянути метод Холецького. Метод Холецького використовується для розв’язування СЛАР з симетричними матрицями (
- 14. Обчислення det(A) на основі LU-розкладу матриці det(A)= det(LU)= det(L) det(U) = Розв’язування СЛАР на основі LU-розкладу
- 15. Для обчислення оберненої матриці необхідно розв’язати n систем лінійних алгебраїчних рівнянь виду: A Z(j)= δ(j), j=1,n
- 16. Обчислення A-1 Знаючи розклад обернену матрицю легко обчислити як
- 17. РОЗВ’ЯЗУВАННЯ ПЕРЕВИЗНАЧЕНИХ СИСТЕМ РІВНЯНЬ Припустимо, що система Ax = b має матрицю A розмірністю m× n
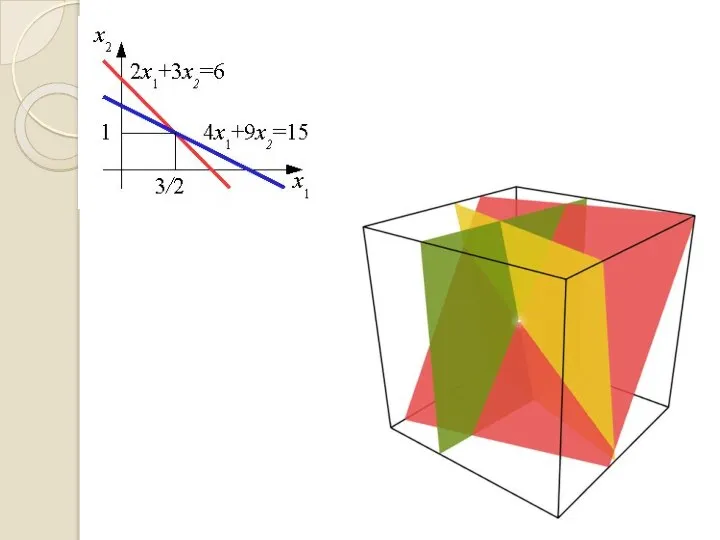
- 18. ТОЧНІСТЬ РОЗВ’ЯЗКУ СЛАР 6,1 x 1 + 3,4 x 2 = 6,1 14,7 x 1 +
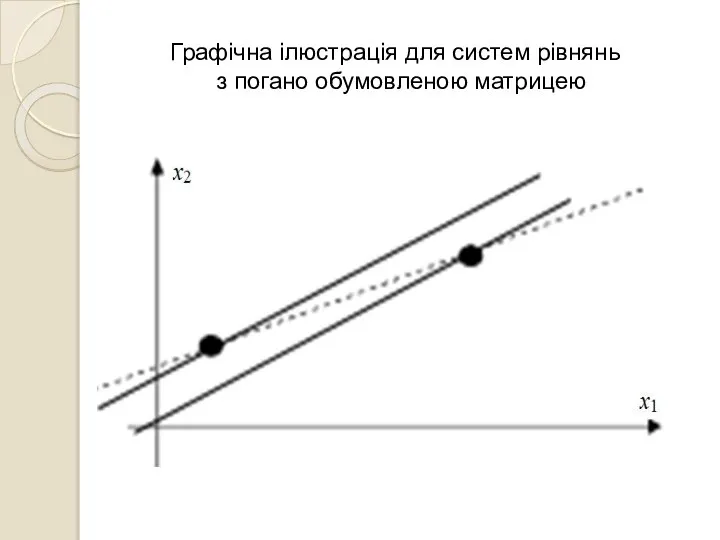
- 19. Графічна ілюстрація для систем рівнянь з погано обумовленою матрицею
- 20. Норми векторів Норма lp ||x||p = (|x1|p + |x2|p +…+|xn|p)1/p Евклидова норма ||x||2 = (|x1|2 +
- 21. Норми матриць Норма lp Евклидова норма Норма l1 Норма l∞
- 22. ВЛАСТИВОСТІ НОРМ векторів: ||x|| ≥ 0 ||x|| = 0 лише для x = 0 || c
- 23. ЧИСЛО ОБУМОВЛЕНОСТІ Нехай x* − точний розв’язок, xн − обчислене (наближене) значення розв’язку, δx = (x*
- 24. ЧИСЛО ОБУМОВЛЕНОСТІ Припустимо, що (A + δA)(x* + δx) = b. Маємо A δx + δA(x*
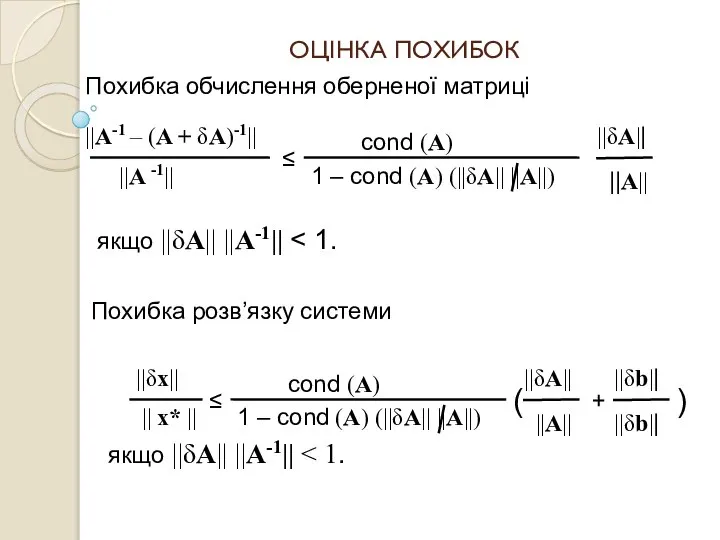
- 25. ОЦІНКА ПОХИБОК Похибка обчислення оберненої матриці ||A-1 – (A + δA)-1|| ||A -1|| ≤ cond (A)
- 27. Скачать презентацию





















 Презентация по математике "Синус , косинус, тангенс и котангенс угла из промежутка [0°; 180°]" -
Презентация по математике "Синус , косинус, тангенс и котангенс угла из промежутка [0°; 180°]" -  Замкнутые линии. Незамкнутые линиии
Замкнутые линии. Незамкнутые линиии 2 класс Математический диктант № 2 Выполнила Кирилова С.Г. Учитель начальных классов Школы «Ученики Пифагора» г. Лимассол, р.Кипр
2 класс Математический диктант № 2 Выполнила Кирилова С.Г. Учитель начальных классов Школы «Ученики Пифагора» г. Лимассол, р.Кипр Рационал сандарды көбейту
Рационал сандарды көбейту Вероятность событий
Вероятность событий Решение тестовых заданий по математике. Подготовка к ГИА
Решение тестовых заданий по математике. Подготовка к ГИА Элементы математической логики. Формулы алгебры логики
Элементы математической логики. Формулы алгебры логики Мультимедийный урок Параллелепипед
Мультимедийный урок Параллелепипед Уравнение касательной. Условие касания
Уравнение касательной. Условие касания Прямая в пространстве
Прямая в пространстве Алгебра. Лекция 4. Теория сравнений – теория остатков
Алгебра. Лекция 4. Теория сравнений – теория остатков « Использование системно-деятельностнoго подхода на уроках математики»
« Использование системно-деятельностнoго подхода на уроках математики» Своя игра по геометрии
Своя игра по геометрии Презентация на тему Теория вероятностей, 9 класс.
Презентация на тему Теория вероятностей, 9 класс. Приближенное решение алгебраических и трансцендентных уравнений. Решение уравнений с одной переменной. Лекция 5
Приближенное решение алгебраических и трансцендентных уравнений. Решение уравнений с одной переменной. Лекция 5 Презентация по математике "Галерея великих" - скачать
Презентация по математике "Галерея великих" - скачать  Средние величины
Средние величины Построение графиков функции y = sinx и y = cosx
Построение графиков функции y = sinx и y = cosx Пропорция. 6 класс
Пропорция. 6 класс Длиннее, короче, одинаковые по длине
Длиннее, короче, одинаковые по длине Упрощение выражений (2)
Упрощение выражений (2) Титло
Титло Интеграл
Интеграл Collision Detection
Collision Detection Распределительные свойства умножения
Распределительные свойства умножения Метод математической индукции
Метод математической индукции Скалярное произведение векторов
Скалярное произведение векторов Презентация на тему Умножение и деление положительных и отрицательных чисел
Презентация на тему Умножение и деление положительных и отрицательных чисел