Содержание
- 3. Здесь μ = M(X) - математическое ожидание, σ2 = D(X) - дисперсия, σ = σ(X) –
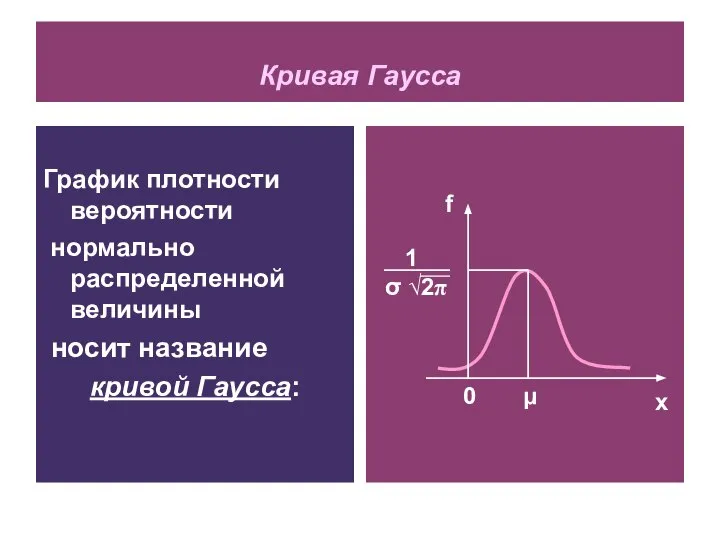
- 4. Кривая Гаусса График плотности вероятности нормально распределенной величины носит название кривой Гаусса: x f 0 μ
- 5. График ее функции распределения – интегральная кривая Гаусса: Интегральная кривая Гаусса F х 1 0
- 6. Введение нормированной нормальной величины Для определения вероятности попадания нормальной СВ в некоторый интервал требуется вычисление интеграла
- 7. НОРМИРОВАННАЯ НОРМАЛЬНАЯ ВЕЛИЧИНА Такая нормальная величина называется нормированной и обозначается Т. Свойства Φ (t) Φ(-∞) =
- 8. Плотность вероятности нормированной нормальной величины
- 9. Функция распределения нормированной нормальной величины
- 10. ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ Φ (t) Приближенные значения Φ (t) для значений аргумента t ≥ 0 вычислены и
- 11. ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ F(X) Значения функции распределения F(х) произвольной нормальной величины можно определить через нормированную путем СПЕЦИАЛЬНОЙ
- 12. Вероятность попадания значений нормальной величины в произвольный интервал Для любой нормальной величины формула имеет следующий вид:
- 13. ПРАВИЛО ТРЕХ СИГМ Вероятность того, что значения нормальной величины распределятся в окрестности ε (« эпсилон »)
- 15. ε = σ Чем больше окрестность ε, тем выше вероятность попадания в нее значений величины Х.
- 16. ε = 2σ, ε = 3σ 2) ε = 2σ. Аналогичный расчет дает вероятность 0,9544 (или
- 18. Скачать презентацию














 6 класс Делители и кратные. Признаки делимости на 2, на 5, на 10. Нестеренко Н.И МОУ СОШ № 4 г. Меленки.
6 класс Делители и кратные. Признаки делимости на 2, на 5, на 10. Нестеренко Н.И МОУ СОШ № 4 г. Меленки. Статистические наблюдения
Статистические наблюдения Матриці, дії з матрицями. Визначники, їх властивості
Матриці, дії з матрицями. Визначники, їх властивості Презентация по математике "Нахождение неизвестного слагаемого" - скачать
Презентация по математике "Нахождение неизвестного слагаемого" - скачать  Системы n линейных уравнений с m неизвестными. Теорема Кронекера-Капелли. Методы их решения. Тема 3
Системы n линейных уравнений с m неизвестными. Теорема Кронекера-Капелли. Методы их решения. Тема 3 Урок по теме. «Формулы сокращенного умножения».
Урок по теме. «Формулы сокращенного умножения».  Урок-презентация в 3 классе учитель: Люлякина И.Ю. МБОУ «СОШ №12» г.Астрахань.
Урок-презентация в 3 классе учитель: Люлякина И.Ю. МБОУ «СОШ №12» г.Астрахань.  Уменьшаемое. Вычитаемое. Разность
Уменьшаемое. Вычитаемое. Разность Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Проценты
Проценты Арифметикалық және геометриялық прогрессиялардың формулаларын пайдалана отырып есептер шығару
Арифметикалық және геометриялық прогрессиялардың формулаларын пайдалана отырып есептер шығару Презентация по математике "Острые и тупые углы" - скачать
Презентация по математике "Острые и тупые углы" - скачать  Основные понятия математической статистики
Основные понятия математической статистики Дробно-линейная функция
Дробно-линейная функция Вписанные и описанные тела
Вписанные и описанные тела Урок 11 Расстояния между прямыми
Урок 11 Расстояния между прямыми  Математические модели и математическое моделирование
Математические модели и математическое моделирование Решение задач с параметрами Выполнила: Матвиенко Елена Валентиновна – учитель математики ГООУ санаторной школы-интерната
Решение задач с параметрами Выполнила: Матвиенко Елена Валентиновна – учитель математики ГООУ санаторной школы-интерната  Математика и спорт
Математика и спорт 13-й порок взрослых или введение в теорию вероятностей
13-й порок взрослых или введение в теорию вероятностей Коэффициенты квадратного уравнения
Коэффициенты квадратного уравнения Прогрессии. Математика в биологии и медицине
Прогрессии. Математика в биологии и медицине Аттестационная работа. Разработка урока-исследования для 5-6 классов по теме «Запись числа. Системы счисления»
Аттестационная работа. Разработка урока-исследования для 5-6 классов по теме «Запись числа. Системы счисления» Развёртки параллелепипеда и куба
Развёртки параллелепипеда и куба Авторы: Атаманова Лиза Нехорошкова Надя
Авторы: Атаманова Лиза Нехорошкова Надя 4 ступень. Математика. Деление. Табличные случаи деления
4 ступень. Математика. Деление. Табличные случаи деления Построение циркулем и линейкой. 7 класс
Построение циркулем и линейкой. 7 класс Аттестационная работа. Образовательная программа внеурочной деятельности «Юный математик»
Аттестационная работа. Образовательная программа внеурочной деятельности «Юный математик»