Содержание
- 2. Тема уроку: Обернена функція
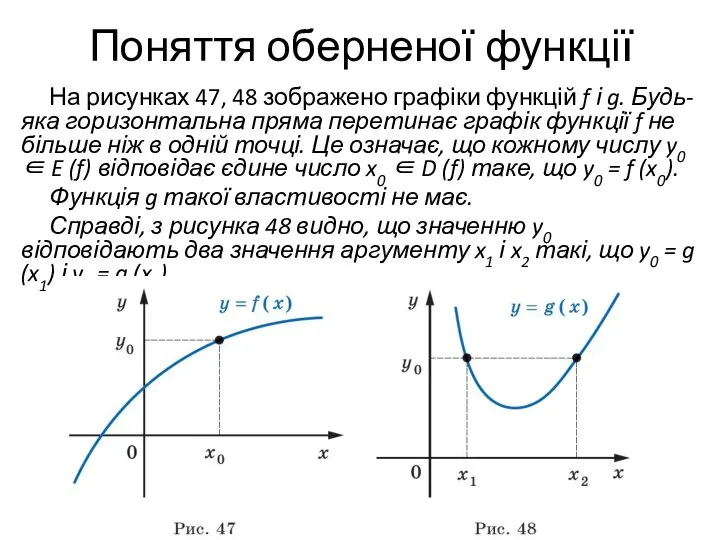
- 3. Поняття оберненої функції На рисунках 47, 48 зображено графіки функцій f і g. Будь-яка горизонтальна пряма
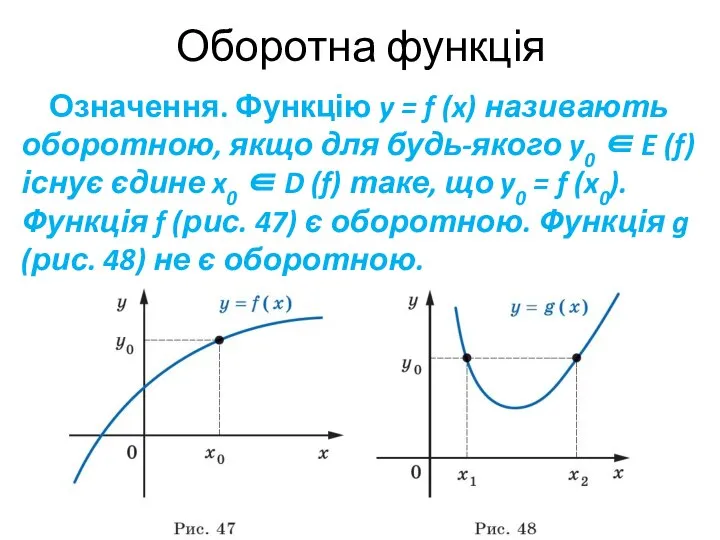
- 4. Оборотна функція Означення. Функцію y = f (x) називають оборотною, якщо для будь-якого y0 ∈ E
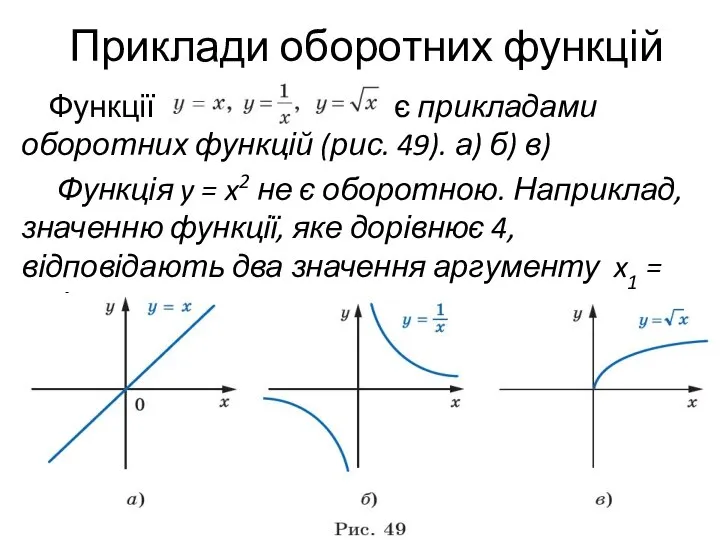
- 5. Приклади оборотних функцій Функції є прикладами оборотних функцій (рис. 49). а) б) в) Функція y =
- 6. Теорема 6.1 Теорема 6.1. Якщо функція є зростаючою (спадною), то вона є оборотною. Доведення. Припустимо, що
- 7. Розглянемо функцію y = f (x), задану таблично: Функція f є оборотною. Поміняємо рядки таблиці місцями
- 8. Взаємно обернені функції Означення. Функції f і g називають взаємно оберненими, якщо: D (f) = E
- 9. Приклад
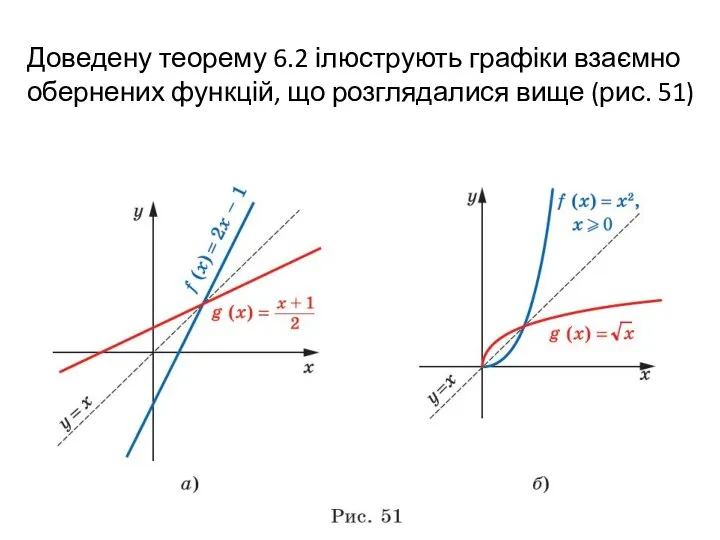
- 12. Доведену теорему 6.2 ілюструють графіки взаємно обернених функцій, що розглядалися вище (рис. 51)
- 14. Первинне закріплення вивченого матеріалу Яку функцію називають оборотною? Сформулюйте теорему про оборотність зростаючої (спадної) функції. Як
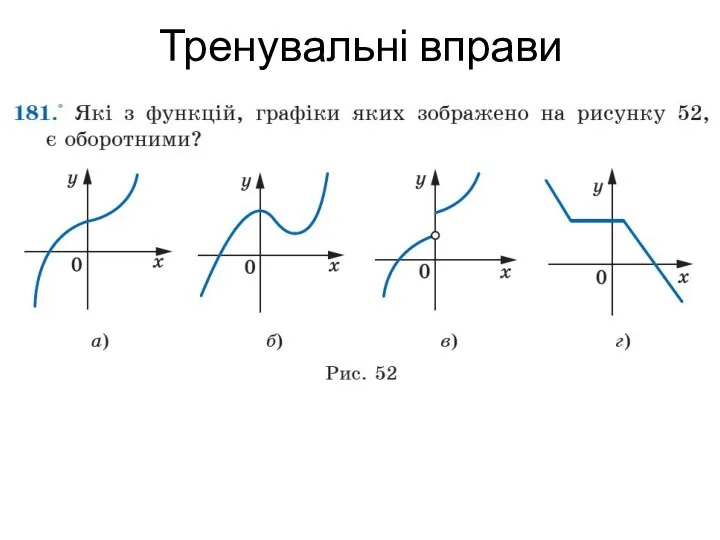
- 15. Тренувальні вправи
- 16. Коментоване виконання вправ
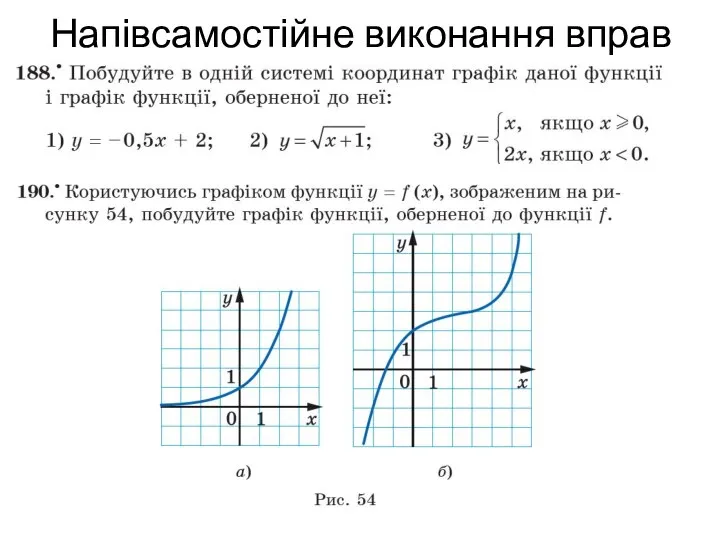
- 17. Напівсамостійне виконання вправ
- 19. Скачать презентацию










 Организация обучения по математике. Принципы отбора содержания и составления дистанционного урока
Организация обучения по математике. Принципы отбора содержания и составления дистанционного урока Сложение чисел с разными знаками 6 класс Выполнила учитель математики ТМБОУ «Дудинская средняя школа №7» Филатова Е.А.
Сложение чисел с разными знаками 6 класс Выполнила учитель математики ТМБОУ «Дудинская средняя школа №7» Филатова Е.А.  Презентация по математике Действия с десятичными дробями
Презентация по математике Действия с десятичными дробями  Синус и тангенс
Синус и тангенс Задачи на разрезание и перекраивание фигур. Урок геометрии для 5 класса
Задачи на разрезание и перекраивание фигур. Урок геометрии для 5 класса Ешение систем линейных уравнений методом крамера
Ешение систем линейных уравнений методом крамера Построение графиков тригонометрических функций
Построение графиков тригонометрических функций Формулы корней квадратных уравнений
Формулы корней квадратных уравнений Без знаний дробей никто не может признаваться знающим арифметику
Без знаний дробей никто не может признаваться знающим арифметику Взаимосвязь математики и окружающего мира в симметрии
Взаимосвязь математики и окружающего мира в симметрии События
События Осевая и центральная симметрии
Осевая и центральная симметрии Геометрическая прогрессия
Геометрическая прогрессия Активные методы и технологии обучения математике в начальной школе
Активные методы и технологии обучения математике в начальной школе Презентация по математике "Упрощение выражений" - скачать бесплатно
Презентация по математике "Упрощение выражений" - скачать бесплатно Задания командам. Треугольники. (7 класс)
Задания командам. Треугольники. (7 класс) Геометрические образы, автоматных отображений
Геометрические образы, автоматных отображений Методология математического моделирования
Методология математического моделирования Приведение подобных слагаемых
Приведение подобных слагаемых Числовые выражения
Числовые выражения Координаты вектора
Координаты вектора Закрепление знаний по теме устный счёт
Закрепление знаний по теме устный счёт Математическая логика и теория алгоритмов
Математическая логика и теория алгоритмов Знаки синуса, косинуса, тангенса и котангенса
Знаки синуса, косинуса, тангенса и котангенса Корреляция. Причинность. Детерминизм
Корреляция. Причинность. Детерминизм Поверхности второго порядка
Поверхности второго порядка Женщины в математике
Женщины в математике Алгебраические преобразования с параметрами Изучение многих физических процессов и геометрических закономерностей часто приво
Алгебраические преобразования с параметрами Изучение многих физических процессов и геометрических закономерностей часто приво